1. 集成学习概述
1.1. 定义
集成学习(Ensemble learning)就是将若干个弱分类器通过一定的策略组合之后产生一个强分类器。 弱分类器(Weak Classifier)指的就是那些分类准确率只比随机猜测略好一点的分类器,而强分类器( Strong Classifier)的分类准确率会高很多。这里的"强"&"弱"是相对的。某些书中也会把弱分类器称 为“基分类器”。
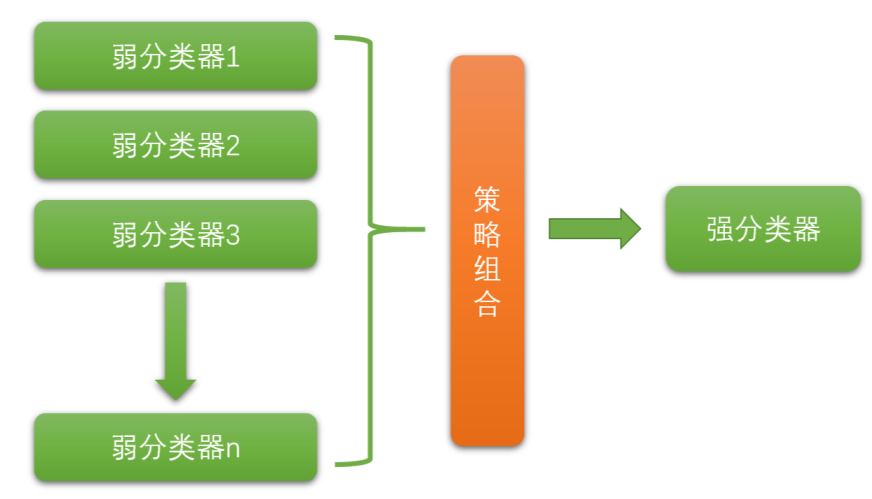
目前集成学习算法的流派主要有两种:
- bagging
- boosting
1.2. bagging
装袋(bagging)又称自主聚集(bootstrap aggregating),是一种根据均匀概率分布从数据集中重复 抽样(有放回的)的技术。每个新数据集和原始数据集的大小相等。由于新数据集中的每个样本都是从 原始数据集中有放回的随机抽样出来的,所以新数据集中可能有重复的值,而原始数据集中的某些样本 可能根本就没出现在新数据集中。
bagging方法的流程,如下图所示:
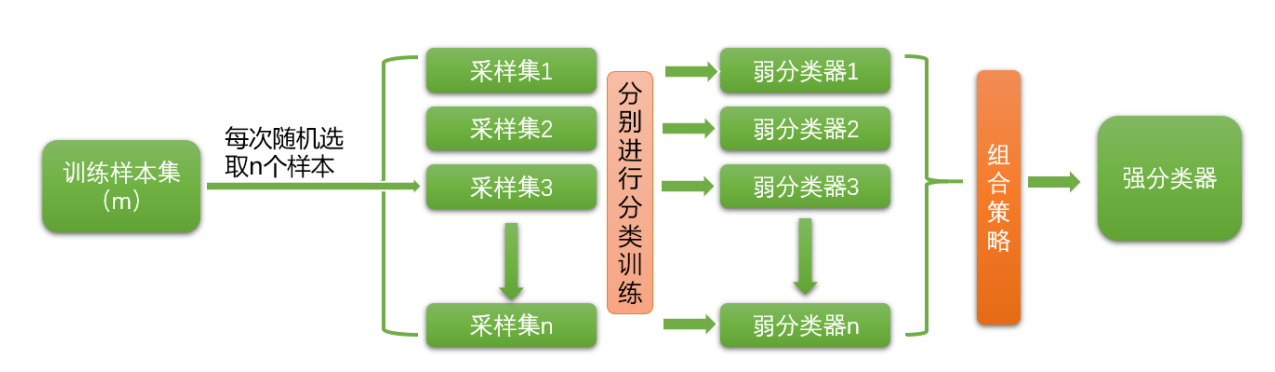
- 有放回的随机抽样:
自主采样法(Bootstap sampling),也就是说对于m个样本的原始数据集,每次 随机选取一个样本放入采样集,然后把这个样本重新放回原数据集中,然后再进行下一个样本的随机抽 样,直到一个采样集中的数量达到m,这样一个采样集就构建好了,然后我们可以重复这个过程,生成 n个这样的采样集。也就是说,最后形成的采样集,每个采样集中的样本可能是重复的,也可能原数据 集中的某些样本根本就没抽到,并且每个采样集中的样本分布可能都不一样。
根据有放回的随机抽样构造的n个采样集,我们就可以对它们分别进行训练,得到n个弱分类器,然后根 据每个弱分类器返回的结果,我们可以采用一定的组合策略得到我们最后需要的强分类器。
bagging方法的代表算法是随机森林,准确的来说,随机森林是bagging的一个特化进阶版,所谓的特 化是因为随机森林的弱学习器都是决策树。所谓的进阶是随机森林在bagging的样本随机采样基础上, 又加上了特征的随机选择,其基本思想没有脱离bagging的范畴。
1.3. boosting
boosting是一个迭代的过程,用来自适应地改变训练样本的分布,使得弱分类器聚焦到那些很难分类的 样本上。它的做法是给每一个训练样本赋予一个权重,在每一轮训练结束时自动地调整权重。
boosting方法的流程,如下图所示:
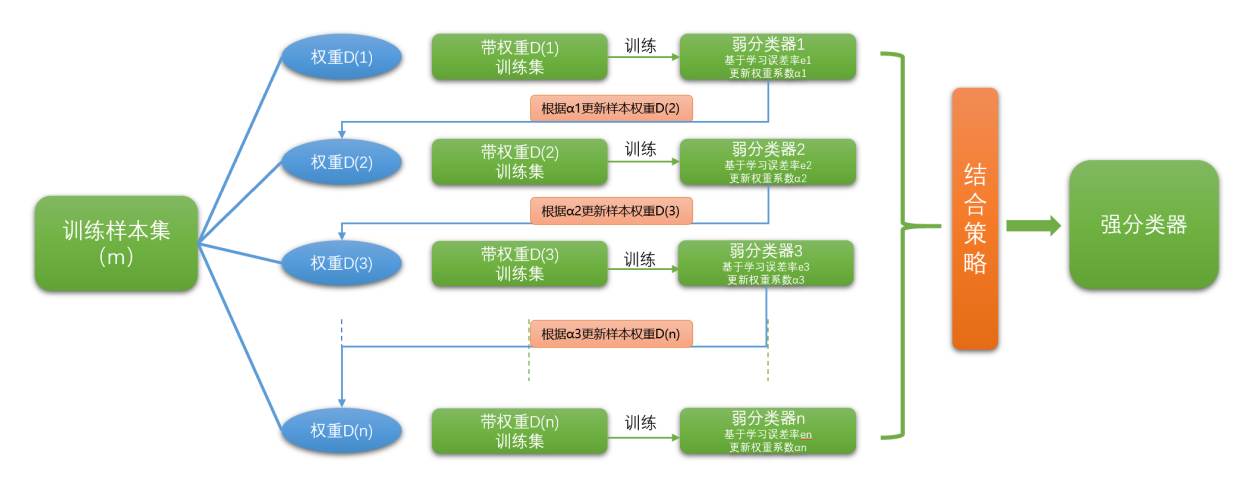
boosting方法的代表算法有Adaboost、GBDT、XGBoost算法
1.4. 结合策略
1.4.1. 平均法
对于数值类的回归预测问题,通常使用的结合策略是平均法,也就是说,对于若干个弱学习器的输出进 行平均得到最终的预测输出。
假设我们最终得到的n个弱分类器为

最简单的平均是算术平均,也就是说最终预测是

如果每个弱分类器有一个权重w,则最终预测是

1.4.2. 投票法
对于分类问题的预测,我们通常使用的是投票法。假设我们的预测类别是

对于任意一个预测样本x,我们的n个弱学习器的预测结果分别是

最简单的投票法是相对多数投票法,也就是我们常说的少数服从多数,也就是n个弱学习器的对样本x的 预测结果中,数量最多的类别 为最终的分类类别。如果不止一个类别获得最高票,则随机选择一个做 最终类别。
稍微复杂的投票法是绝对多数投票法,也就是我们常说的要票过半数。在相对多数投票法的基础上,不 光要求获得最高票,还要求票过半数。否则会拒绝预测。
更加复杂的是加权投票法,和加权平均法一样,每个弱学习器的分类票数要乘以一个权重,最终将各个 类别的加权票数求和,最大的值对应的类别为最终类别。
1.4.3. 学习法
前两种方法都是对弱学习器的结果做平均或者投票,相对比较简单,但是可能学习误差较大,于是就有 了学习法这种方法,对于学习法,代表方法是stacking,当使用stacking的结合策略时, 我们不是对弱 学习器的结果做简单的逻辑处理,而是再加上一层学习器,也就是说,我们将训练集弱学习器的学习结 果作为输入,将训练集的输出作为输出,重新训练一个学习器来得到最终结果。
在这种情况下,我们将弱学习器称为初级学习器,将用于结合的学习器称为次级学习器。对于测试集, 我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的 预测结果。
2. AdaBoost
Adaboost是adaptive boosting(自适应boosting)的缩写。算法步骤如下:

2.1. 计算样本权重
赋予训练集中每个样本一个权重,构成权重向量D,将权重向量D初始化相等值。设定我们有m个样本,每个样本的权重都相等,则权重为

2.2. 计算错误率
在训练集上训练出一个弱分类器,并计算分类器的错误率:

2.3. 计算弱分离器权重
为当前分类器赋予权重值alpha,则alpha计算公式为:

2.4. 调整权重值
根据上一次训练结果,调整权重值(上一次分对的权重降低,分错的权重增加
如果第i个样本被正确分类,则该样本权重更改为:

如果第i个样本被分错,则该样本权重更改为:

把上面两个公式汇整成一个:

之后,在同一数据集上再一次训练弱分类器,然后循环上述过程,直到训练错误率为0,或者弱分类器 的数目达到指定值。
2.5. 结果
循环结束后,我们可以得到我们的强分类器的预测结果:

3. 基于单层决策树构建弱分类器
单层决策树(decision stump)也称决策树桩,是一种简单的决策树。我们已经讲过决策树的相 关原理了,接下来我们一起来构建一个单层决策树,它仅仅基于单个特征来做决策。由于这棵树只有一 次分裂过程,因此它实际上就是一个树桩。
3.1. 构建数据集
- 我们先构建一个简单数据集来确保我们写出的函数能够正常运行。
import pandas as pd
import numpy as np
# 获得特征矩阵和标签矩阵
def get_Mat(path):
dataSet = pd.read_table(path,header = None)
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
return xMat,yMat
xMat,yMat = get_Mat('simpdata.txt')
- 构建数据可视化函数,并运行查看数据分布
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['simhei']
%matplotlib inline
# 数据集可视化函数
def showPlot(xMat,yMat):
x=np.array(xMat[:,0])
y=np.array(xMat[:,1])
label = np.array(yMat)
plt.scatter(x,y,c=label)
plt.title('单层决策树测试数据')
plt.show()
showPlot(xMat,yMat)

3.2. 构建单层决策树
我们会建立两个函数来实现我们的单层决策树:
第一个函数用来测试是否有某个值小于或者大于我们正在测试的阈值。
"""
函数功能:单层决策树分类函数
参数说明:
xMat: 特征矩阵
i: 第i列,也就是第几个特征
Q: 阈值
S: 标志
返回:
re: 分类结果
"""
def Classify0(xMat,i,Q,S):
re = np.ones((xMat.shape[0],1)) # 初始化re为1
if S == 'lt':
re[xMat[:,i] <= Q] = -1 # 如果小于阈值,则赋值为-1
else:
re[xMat[:,i] > Q] = -1 # 如果大于阈值,则赋值为-1
return re
第二个函数稍微复杂一些,会在一个加权数据集中循环,并找到具有最低错误率的单层决策树
"""
函数功能:找到数据集上最佳的单层决策树
参数说明:
xMat:特征矩阵
yMat:标签矩阵
D:样本权重
返回:
bestStump:最佳单层决策树信息
minE:最小误差
bestClas:最佳的分类结果
"""
def get_Stump(xMat,yMat,D):
m,n = xMat.shape # m为样本个数,n为特征数
Steps = 10 # 初始化一个步数
bestStump = {} # 用字典形式来储存树桩信息
bestClas = np.mat(np.zeros((m,1))) # 初始化分类结果为1
minE = np.inf # 最小误差初始化为正无穷大
for i in range(n): # 遍历所有特征
Min = xMat[:,i].min() # 找到特征中最小值
Max = xMat[:,i].max() # 找到特征中最大值
stepSize = (Max - Min) / Steps # 计算步长
for j in range(-1, int(Steps)+1):
for S in ['lt', 'gt']: # 大于和小于的情况,均遍历。lt:less than,gt:greater than
Q = (Min + j * stepSize) # 计算阈值
re = Classify0(xMat, i, Q, S) # 计算分类结果
err = np.mat(np.ones((m,1))) # 初始化误差矩阵
err[re == yMat] = 0 # 分类正确的,赋值为0
eca = D.T * err # 计算误差
# print(f'切分特征: {i}, 阈值:{np.round(Q,2)}, 标志:{S}, 权重误差:{np.round(eca,3)}')
if eca < minE: # 找到误差最小的分类方式
minE = eca
bestClas = re.copy()
bestStump['特征列'] = i
bestStump['阈值'] = Q
bestStump['标志'] = S
return bestStump,minE,bestClas
测试函数并运行查看结果:
m = xMat.shape[0]
D = np.mat(np.ones((m, 1)) / m) # 初始化样本权重(每个样本权重相等)
bestStump,minE,bestClas= get_Stump(xMat,yMat,D)
4. AdaBoost代码
用python代码来实现完整版AdaBoost算法
"""
函数功能:基于单层决策树的AdaBoost训练过程
参数说明:
xMat:特征矩阵
yMat:标签矩阵
maxC:最大迭代次数
返回:
weakClass:弱分类器信息
aggClass:类别估计值(其实就是更改了标签的估计值)
"""
def Ada_train(xMat, yMat, maxC = 40):
weakClass = []
m = xMat.shape[0]
D = np.mat(np.ones((m, 1)) / m) # 初始化权重
aggClass = np.mat(np.zeros((m,1)))
for i in range(maxC):
Stump, error, bestClas = get_Stump(xMat, yMat,D) # 构建单层决策树
# print(f"D:{D.T}")
alpha=float(0.5 * np.log((1 - error) / max(error, 1e-16))) # 计算弱分类器权重alpha
Stump['alpha'] = np.round(alpha,2) # 存储弱学习算法权重,保留两位小数
weakClass.append(Stump) # 存储单层决策树
# print("bestClas: ", bestClas.T)
expon = np.multiply(-1 * alpha *yMat, bestClas) # 计算e的指数项
D = np.multiply(D, np.exp(expon))
D = D / D.sum() # 根据样本权重公式,更新样本权重
aggClass += alpha * bestClas #更新累计类别估计值
# print(f"aggClass: {aggClass.T}" )
aggErr = np.multiply(np.sign(aggClass) != yMat, np.ones((m,1)))# 计算误差
errRate = aggErr.sum() / m
# print(f"分类错误率: {errRate}")
if errRate == 0: break # 误差为0,退出循环
return weakClass, aggClass
- 运行函数,查看结果:
weakClass, aggClass =Ada_train(xMat, yMat, maxC = 40)
weakClass
aggClass
5. 基于AdaBoost的分类
这里我们使用弱分类器的加权求和来计算最后的结果。
"""
函数功能:AdaBoost分类函数
参数说明:
data: 待分类样例
classifys:训练好的分类器
返回:
分类结果
"""
def AdaClassify(data,weakClass):
dataMat = np.mat(data)
m = dataMat.shape[0]
aggClass = np.mat(np.zeros((m,1)))
for i in range(len(weakClass)): # 遍历所有分类器,进行分类
classEst = Classify0(dataMat,
weakClass[i]['特征列'],
weakClass[i]['阈值'],
weakClass[i]['标志'])
aggClass += weakClass[i]['alpha'] * classEst
# print(aggClass)
return np.sign(aggClass)
- 结果
AdaClassify([0,0],weakClass)
本文由mdnice多平台发布