开启掘金成长之旅！这是我参与「掘金日新计划·2月更文挑战」的第16天，点击查看活动详情

2020(CCPC)-网选赛 1011 3×3 Convolution (HDOJ 6898)

乍一看，很难，仔细一分析，十分简单，解析如下：

这道题是一个简单的迭代。我们输入K'通过下面这个公式，将K'转换为K。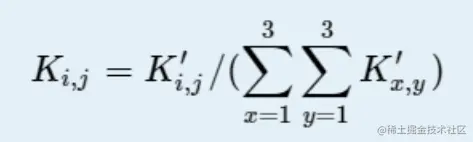

Example：

假设 $\left[ \begin{matrix} \frac{1}{3} & 0 & 0 \\ 0 & \frac{1}{3} & 0 \\ 0 & 0 & \frac{1}{3} \end{matrix} \right]$，A=$\left[ \begin{matrix} 1 & 2 \\3 & 4\\\end{matrix} \right]$，$n=2$

$C_{1,1}=\sum_{i=1}^{2}\sum_{j=1}^{2}A_{i,j}K_{i,j}=A_{1,1}K_{1,1}+A_{2,2}K_{2,2}=1×\frac{1}{3}+4×\frac{1}{3}=\frac{5}{3}$

$C_{1,2}=\sum_{i=1}^{2}\sum_{j=1}^{1}A_{i,j+1}K_{i,j}=A_{1,2}K_{1,1}=2×\frac{1}{3}=\frac{2}{3}$

$C_{2,1}=\sum_{i=1}^{1}\sum_{j=1}^{2}A_{i,j}K_{i,j}=A_{21}K_{11}=3×\frac{1}{3}=1$

$C_{2,2}=\sum_{i=1}^{1}\sum_{j=1}^{1}A_{i+1,j}K_{i,j}=A_{22}K_{11}=4×\frac{1}{3}=\frac{4}{3}$

$C^1=C(A,K)= \left[ \begin{matrix} \frac{5}{3} & \frac{2}{3} \\ 1 & \frac{4}{3} \end{matrix} \right]$

$C^2=C(C',K)$

$C^2_{1,1}=\sum_{i=1}^{2}\sum_{j=1}^{2}C'_{i,j}K_{i,j}=C'_{1,1}K_{1,1}+C'_{2,2}K_{2,2}=\frac{5}{3}×\frac{1}{3}+\frac{4}{3}×\frac{1}{3}=1$

$C^2_{1,1}=\sum_{i=1}^{2}\sum_{j=1}^{1}C'_{i,j+1}K_{i,j}=\frac{2}{9}$

$C^2_{1,1}=1×3=\frac{1}{3}$

$C^2_{2,2}=\frac{4}{9}$

设$lim_{n→∞}C^n(A,K)=\left[ \begin{matrix} a & b \\ c & d \end{matrix} \right]$

$b=lim_{n→∞}(\frac{1}{3})^n\frac{2}{3}=0,\;\;\;\;\;\;\;\;\; c=lim_{n→∞}1×(\frac{1}{3})^n=0,\;\;\;\;\;\;\;d=lim_{n→∞}\frac{4}{3}×\frac{1}{3}=0$

同理：$a=lim_{n→∞}(\frac{1}{3})^n×C($常数$)=0$

②同理： 如果输入的K‘不为0的数只有一个，那么通过迭代，最终的结果是原矩阵。所以输出第一个输入的矩阵即可。

综上所述，答案如下:

刚开始输出一个数N，输入一个N×N的二维数组

再输入一个3×3的二维数组：

如果这个二维数组之中，不为零的数字 ≥ 2，则输出一个全为0的二维数组，如果不为零的数字 ＜ 2，那么原样输出第一轮输入的二维数组。

注意： 这道题卡输出矩阵最后一个数，不能有空格！！！

const int N = 1000;
int a[N][N];
int b[N][N];
int main() {
	int t, cin >> t;
	while(t--) {
		int n = read();
		int flag = 0;
		for(int i = 0;i < n;i++)
			for(int j = 0;j < n;j++)
				cin >> a[i][j];
		for(int i = 0;i < 3; i++) {
			for(int j = 0; j < 3;j++) {
				cin >> b[i][j];
				if(b[i][j] != 0) flag++;
			}
		}
		if (flag > 1) {
			for (int i = 0;i < n; i++) {
				for (int j = 0;j < n - 1; j++)
				    cout << 0 << " ";
				cout << 0;
				cout << endl;
			}
		} else {
			for (int i = 0;i < n;i++) {
				for (int j = 0;j < n - 1; j++)
					cout << a[i][j] << " ";
				cout << a[i][n - 1];
				cout << endl;
			}
		}
	}
	return 0;
}