一、介绍

1.一般形式

指数族分布有：高斯分布、伯努利分布、二项分布、泊松分布、beta分布、Dirichlet分布、gamma分布等。

指数族分布的一般形式：

$$P(x|\eta )=h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \}$$

其中：

• $\eta$：参数向量；
• $\phi (x)$：充分统计量，Sufficient statistic；
• $A(\eta )$：log partition function（log配分函数）
• $h(x)$：不很重要，通常取1。

2.配分函数

通常如果我们得到一个可以表达分布的函数 $\hat{P}(x \mid \theta)$ 但是其积分不为 1 ，需要除以一个归一化 因子 $z$ 来将其归一，这个归一化因子 $z$ 就是配分函数， $z$ 取值为 $\hat{P}(x \mid \theta)$ 的积分:

解释一下为什么 $A(\eta)$ 叫log配分函数：

因此 $\exp \{A(\eta)\}$ 就是配分函数， $A(\eta)$ 就是log配分函数。

3.指数族分布的特点、模型和应用

• 充分统计量

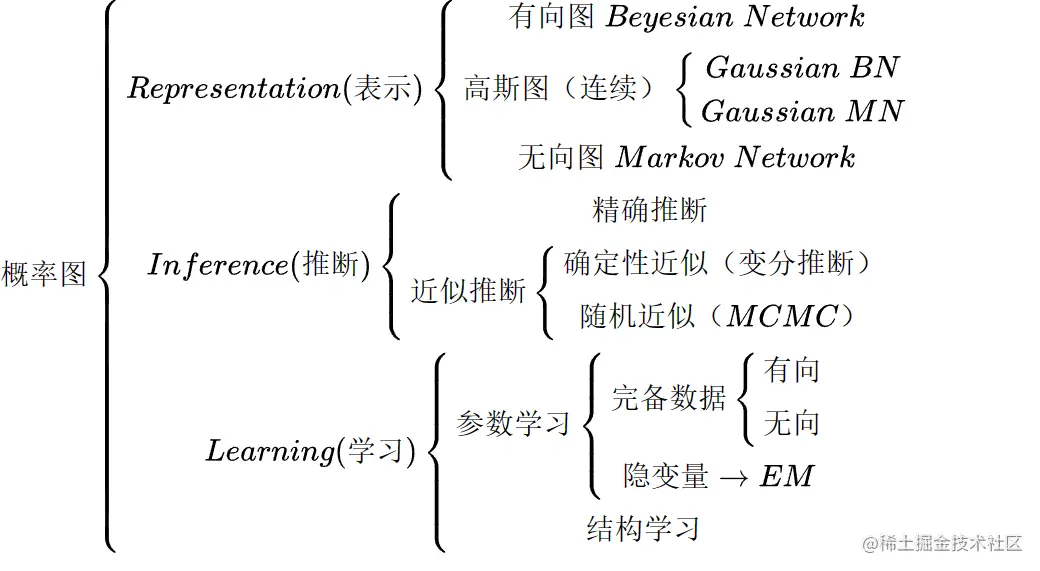
$\phi (x)$是充分统计量。

什么是充分统计量？举例来说，对于从一些从高斯分布中抽取出来的样本$x_{1},x_{2},\cdots ,x_{N}$，以下统计量就是充分统计量：

$$\phi (x)=\begin{pmatrix} \sum_{i=1}^{N}x_{i}\\ \sum_{i=1}^{N}x_{i}^{2} \end{pmatrix}$$

因为通过上述统计量可以计算样本的均值和方差进而得到其明确的分布。

有了充分统计量就可以将样本丢掉，从而节省了空间，对online learning有重要意义。

• 共轭

$$P(z|x)=\frac{P(x|z)P(z)} {\int _{z}P(x|z)P(z)\mathrm{d}z}$$

在上面的贝叶斯公式中由于分母 $\int_z P(x \mid z) P(z) \mathrm{d} z$ 积分难或者 $P(z \mid x)$ 的形式太复杂，因 此直接求 $P(z \mid x)$ 是很困难的，因此求 $E_{P(z \mid x)}[f(z)]$ 也是很困难的，所以人们想了很多办法 比如近似推断 (变分推断、MCMC等)，这些方法的提出都是因为上述积分难的问题。 共轭的概念是指在给定一个特殊的似然 $(P(x \mid z))$ 的情况下，后验 $(P(z \mid x))$ 与先验 ( $P(z))$ 会有一个形式相同的分布，这也就解决了上述积分困难的问题，避免了求分母上的积分项常数。 举个例子:

• 最大熵

给出先验 $P(z)$ 的一些方法包括: ①共轭 $\rightarrow$ 计算上的方便； ②最大熵 $\rightarrow$ 无信息先验; ③Jerrif。

最大熵原理给出了一种定义先验的方式，可以使得参数更加地随机。

• 广义线性模型

广义线性模型中出现的一些概念：

• 概率图模型

无向图中的RBM（限制玻尔兹曼机）应用到了指数族分布。

二、高斯分布的指数族分布形式

以一维高斯分布为例，将高斯分布整理成指数族分布的形式：

$$P(x|\theta )=\frac{1}{\sqrt{2\pi }\sigma }exp\left \{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}\right \}\; \; \theta =(u,\sigma ^{2})\\ =\frac{1}{\sqrt{2\pi \sigma ^{2}}}exp\left \{-\frac{1}{2\sigma ^{2}}(x^{2}-2\mu x+\mu ^{2})\right \}\\ =exp\left \{log(2\pi \sigma ^{2})^{-\frac{1}{2}}\right \}exp\left \{-\frac{1}{2\sigma ^{2}}(x^{2}-2\mu x)-\frac{\mu ^{2}}{2\sigma ^{2}}\right \}\\ =exp\left \{log(2\pi \sigma ^{2})^{-\frac{1}{2}}\right \}exp\left \{-\frac{1}{2\sigma ^{2}}\begin{pmatrix} -2\mu & 1 \end{pmatrix}\begin{pmatrix} x\\ x^{2} \end{pmatrix}-\frac{\mu ^{2}}{2\sigma ^{2}}\right \}\\ =exp\left \{\underset{\eta ^{T}}{\underbrace{\begin{pmatrix} \frac{\mu }{\sigma ^{2}} & -\frac{1}{2\sigma ^{2}} \end{pmatrix}}}\underset{\phi (x)}{\underbrace{\begin{pmatrix} x\\ x^{2} \end{pmatrix}}}-\underset{A(\eta )}{\underbrace{(\frac{\mu ^{2}}{2\sigma ^{2}}+\frac{1}{2}log2\pi \sigma ^{2})}}\right \}$$

然后即可获得$\eta$和$\theta$的关系：

$$\eta =\begin{pmatrix} \eta _{1}\\ \eta _{2} \end{pmatrix}=\begin{pmatrix} \frac{\mu }{\sigma ^{2}}\\ -\frac{1}{2\sigma ^{2}} \end{pmatrix}\\ \left\{\begin{matrix} \eta _{1}=\frac{\mu }{\sigma ^{2}}\\ \eta _{2}=-\frac{1}{2\sigma ^{2}} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} \mu =-\frac{\eta _{1}}{2\eta _{2}}\\ \sigma ^{2}=-\frac{1}{2\eta _{2}} \end{matrix}\right.$$

将$\eta$代入$A(\eta )$可以得到如下结果：

$$A(\eta )=-\frac{\eta _{1}^{2}}{4\eta _{2}}+\frac{1}{2}log(2\pi \cdot -\frac{1}{2\eta _{2}})\\ =\frac{\eta _{1}^{2}}{4\eta _{2}}+\frac{1}{2}log(-\frac{\pi }{2\eta _{2}})$$

由此就将高斯分布整理成了指数族分布的形式：

$$P(x|\theta )=h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \} \\ h(x)=1\; \eta =\begin{pmatrix} \eta _{1}\\ \eta _{2} \end{pmatrix}=\begin{pmatrix} \frac{\mu }{\sigma ^{2}}\\ -\frac{1}{2\sigma ^{2}} \end{pmatrix}\; \phi (x)=\begin{pmatrix} x\\ x^{2} \end{pmatrix}\; A(\eta )=\frac{\eta _{1}^{2}}{4\eta _{2}}+\frac{1}{2}log(-\frac{\pi }{2\eta _{2}})$$

三、对数配分函数与充分统计量

通过对指数族分布的通用形式进行整理，可以得出对数配分函数与充分统计量 的特定关系：

$$P(x|\eta )=h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \}\\ =\frac{1}{exp\left \{A(\eta )\right \}}h(x)exp\left \{\eta ^{T}\phi (x)\right \}\\ 由前面介绍的内容可知配分函数exp\left \{A(\eta )\right \}=\int h(x)exp\left \{\eta ^{T}\phi (x)\right \}\mathrm{d}x\\ \Rightarrow \frac{\partial exp\left \{A(\eta )\right \}}{\partial \eta }=\frac{\partial (\int h(x)exp\left \{\eta ^{T}\phi (x)\right \}\mathrm{d}x)}{\partial \eta }\\ \Rightarrow exp\left \{A(\eta )\right \}A^{'}(\eta )=\int h(x)exp\left \{\eta ^{T}\phi (x)\right \}\phi (x)\mathrm{d}x\\ \Rightarrow A^{'}(\eta )=\frac{\int h(x)exp\left \{\eta ^{T}\phi (x)\right \}\phi (x)\mathrm{d}x}{exp\left \{A(\eta )\right \}}\\ =\int \underset{P(x|\eta )}{\underbrace{h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \}}}\phi (x)\mathrm{d}x\\ =\int P(x|\eta )\phi (x)\mathrm{d}x\\ =E_{P(x|\eta )}[\phi (x)]$$

类似地，继续对$A(\eta )$求二阶导数:

$$A^{''}(\eta )=\frac{\partial (\int h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \}\phi (x)\mathrm{d}x)}{\partial \eta }\\ =\int \underset{P(x|\eta )}{\underbrace{h(x)exp\left \{\eta ^{T}\phi (x)-A(\eta )\right \}}}(\phi (x)-A^{'}(\eta ))\phi (x)\mathrm{d}x\\ =\int P(x|\eta )(\phi (x)-E_{P(x|\eta )}[\phi (x)])\phi (x)\mathrm{d}x\\ =\int P(x|\eta )\phi ^{2}(x)-E_{P(x|\eta )}[\phi (x)]P(x|\eta )\phi (x)\mathrm{d}x\\ =\int P(x|\eta )\phi ^{2}(x)\mathrm{d}x-E_{P(x|\eta )}[\phi (x)]\int P(x|\eta )\phi (x)\mathrm{d}x\\ =E_{P(x|\eta )}[\phi ^{2}(x)]-E_{P(x|\eta )}^{2}[\phi (x)]\\ =Var_{P(x|\eta )}[\phi (x)]\\ 由于方差\geq 0，则A^{''}(\eta )\geq 0，因此A(\eta )是凸函数。$$

四、极大似然估计与充分统计量

上述推导都是在无样本条件下进行的，在有样本的情况下我们也可以通过极大似然估计法来获得一些特定的关系，假设有如下数据：

$$D=\left \{x_{1},x_{2},\cdots ,x_{N}\right \}$$

然后使用极大似然估计法求解$\eta$：

$$\eta _{MLE}=\underset{\eta }{argmax}\; logP(D|\eta )\\ =\underset{\eta }{argmax}\; log\prod_{i=1}^{N}P(x_{i}|\eta )\\ =\underset{\eta }{argmax}\sum_{i=1}^{N}logP(x_{i}|\eta )\\ =\underset{\eta }{argmax}\sum_{i=1}^{N}log[h(x_{i})exp\left \{\eta ^{T}\phi (x_{i})-A(\eta )\right \}]\\ =\underset{\eta }{argmax}\sum_{i=1}^{N}[\underset{与\eta 无关}{\underbrace{log\; h(x_{i})}}+\eta ^{T}\phi (x_{i})-A(\eta )]\\ =\underset{\eta }{argmax}\sum_{i=1}^{N}[\eta ^{T}\phi (x_{i})-A(\eta )]\\ \frac{\partial \sum_{i=1}^{N}[\eta ^{T}\phi (x_{i})-A(\eta )]}{\partial \eta }\\ =\sum_{i=1}^{N}\frac{\partial [\eta ^{T}\phi (x_{i})-A(\eta )]}{\partial \eta }\\ =\sum_{i=1}^{N}[\phi (x_{i})-A^{'}(\eta )]\\ =\sum_{i=1}^{N}\phi (x_{i})-NA^{'}(\eta )\\ =0\\ \Rightarrow A^{'}(\eta _{MLE})=\frac{1}{N}\sum_{i=1}^{N}\phi (x_{i})$$

$\eta_{M L E}$ 就可以通过求 $A^{\prime}(\eta)$ 的反函数求出来。这说明 $\phi\left(x_i\right)$ 是充分统计量，因为只需要记录 $\frac{1}{N} \sum_{i=1}^N \phi\left(x_i\right)$ 这一个值就可以求出 $\eta$ ，进而通过 $\eta$ 求出所有的参数。

五、最大熵

1.概述

首先定义信息量和熵：

$$信息量：-log\; p(x)\\ 熵：\\ H[P]=E[-log\; p(x)]=\int -p(x)log\; p(x)\mathrm{d}x(连续)\\ H[P]=E[-log\; p(x)]=-\sum_{i=1}^{N}p(x)log\; p(x)(离散)$$

2.离散情况下的最大熵

假设$x$是离散的：

x	1	2	$\cdots$	k
P	$p_{1}$	$p_{2}$	$\cdots$	$p_{k }$

通过求解以下约束优化问题可以求得使得离散情况下熵最大的分布：

$$\left\{\begin{matrix} max\; H[P]=max-\sum_{i=1}^{k}p_{i}log\; p_{i} \\ s.t.\; \sum_{i=1}^{k}p_{i}=1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} min\sum_{i=1}^{k}p_{i}log\; p_{i}\\ s.t.\; \sum_{i=1}^{k}p_{i}=1 \end{matrix}\right.$$

使用拉格朗日乘子法进行求解：

$$L(P,\lambda )=\sum_{i=1}^{k}p_{i}log\; p_{i}+\lambda (1-\sum_{i=1}^{k}p_{i})\\ \frac{\partial L}{\partial p_{i}}=log\; p_{i}+p_{i}\frac{1}{p_{i}}-\lambda =log\; p_{i}+1-\lambda =0\\ \Rightarrow \hat{p}_{i}=exp(\lambda -1)\\ 也就是说每个\hat{p}_{i}都等于exp(\lambda -1)，由\sum_{i=1}^{k}p_{i}=1可以得到：\\ \hat{p}_{1}=\hat{p}_{2}=\cdots =\hat{p}_{k}=\frac{1}{k}\\ \therefore P(x)是均匀分布。$$

离散情况下均匀分布会使得熵最大。也就是说在没有任何已知条件约束的情况下均匀分布的熵最大。

3.最大熵原理

上一部分得出在无任何已知的情况下的最大熵对应的分布为均匀分布，而在满足一定的约束（已知事实）的条件下就要使用最大熵原理来进行求解。

首先要说明已知事实指的就是我们已经有了一部分数据：

$$Data=\left \{x_{1},x_{2},\cdots ,x_{N}\right \}$$

然后根据数据我们可以定义其经验分布(empirical distribution)：

$$\hat{p}(x=n)=\hat{p}(n)=\frac{count(n)}{N}$$

通过该分布可以获得数据的一些属性，比如 $E_{\hat{p}}[x], \operatorname{Var}_{\hat{p}}[x], \cdots$ 。另外我们假设 $f(x)$ 是任意关于 $x$ 的函数向量，满足:

也就是说现在需要满足上述约束条件，于是在该约束下求解最大熵的分布就转换成了一个约束优化问题:

然后就可以使用拉格朗日乘子法进行求解，首先定义拉格朗日函数：

接着对 $p(x)$ 进行求导，这里指的是对每个 $p\left(x_i\right)$ 进行求导:

显示 $p(x)$ 是一个指数族分布，因此对于连续变量 $x$ ，其在满足既定事实的条件下对应的最大熵的分布是一个指数族分布。

六、总结

更多其他概率分布不再进行一一推导，总结一下服从指数族分布的建模场景：

1.伯努利分布：对0、1问题建模

2.多项式分布：对有K个离散结果事件建模

3.泊松分布：对计数过程进行建模。如网站访问量,商店顾客数量等。

4.指数分布与伽马分布：对有间隔的正数进行建模

5.贝塔分布：对小数建模

6.Dirichlet分布：对概率分布建模

7.Wishart分布：协方差矩阵的分布

8.高斯分布：对连续问题建模

“开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 5 天，点击查看活动详情”