一、简介
从计算的角度,该方法叫Kernel Trick:避免一步一步先把φ(x)求出,再把内积求出来,而是一步到位,直接把样本点带进核方法就可以把内积求出来。减少计算量
从思想的角度,该方法叫Kernel Method:把一个低维空间的非线性问题转化到高维空间的线性问题,利用核函数的性质来求解。
该部分最重要的叫做Kernel Function,它的来历就是因为在我们做分类问题时,例如非线性的不可分给我们带来了一些困境,我们可以使用高维转换进而使用Kernel Function去解决它,又或者是对偶表示带来内积,如果你是高维空间,那么φ(x)就很难求,如果我们先去找到一个核函数,就能直接求出内积(核函数蕴含了一个非线性转换以及非线性转换后的一个内积)
接下来我们就详细的介绍一下核方法涉及到的一些知识点。
二、线性不可分问题
有时线性可分的数据夹杂一点噪声,可以通过改进算法来实现分类,比如感知机的口袋算法和支持向量机的软间隔。但是有时候数据往往完全不是线性可分的,比如下面这种情况:
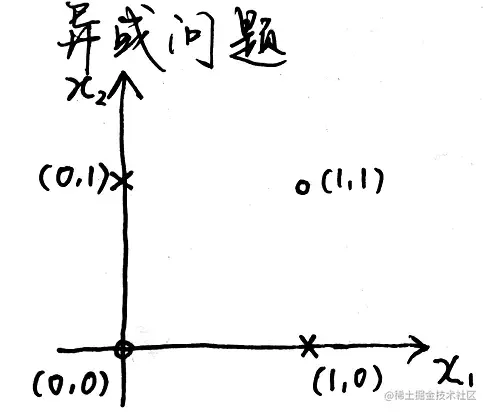
在异或问题中数据往往不是线性可分的,但通过将数据映射到高维空间后就可以实现线性可分。可以认为高维空间中的数据比低维空间的数据更易线性可分。对于异或问题,我们可以通过寻找一个映射ϕ(x)将低维空间中的数据x映射成高维空间中的z来实现数据的线性可分,例如:
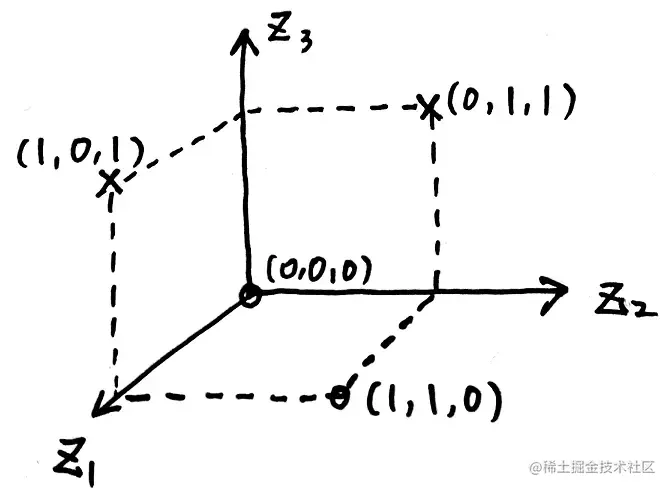
二维x=(x1,x2)→ϕ(x)三维z=(x1,x2,(x1−x2)2)
然后在新的空间中,该数据就可以实现线性可分:
三、核方法的引出
映射到高维空间以后出现的问题是计算复杂度的加大,例如在支持向量机的求解过程中求解的优化问题可以转换为如下的优化问题:
{λmin21∑i=1N∑j=1NλiλjyiyjxiTxj−∑i=1Nλi,i=1,2,⋯,Nλi≥0,i=1,2,⋯,N
将数据映射到高维空间后也就需要求解以下优化问题:
{λmin21∑i=1N∑j=1Nλiλjyiyjϕ(xi)Tϕ(xj)−∑i=1Nλi,i=1,2,⋯,Nλi≥0,i=1,2,⋯,N
将数据拓展到高维的方法可以用来解决完全非线性的问题:
| 线性可分 | 允许一点点错误 | 严格非线性 |
|---|
| PLA | Pocket Algorithm | ϕ(x)+PLA |
| Hard-Margin SVM | Soft-Margin SVM | ϕ(x)+Hard-Margin SVM(Kernel SVM) |
然而在上面的方法中如果先将 ϕ(xi) 与 ϕ(xj) 计算出来然后再做点积,由于维度特别高加之得到 ϕ(xi) 与 ϕ(xj) 也需要计算量,因此计算量是相当大的,因此就有了核方法。
通过使用核函数我们可以直接得到 ϕ(xi) 与 ϕ(xj) 的内积,正定核函数定义如下:
∀x,x′∈X,∃ϕ∈H:x↦z, s.t. K(x,x′)=ϕ(xi)Tϕ(xj)=⟨ϕ(xi),ϕ(xj)⟩, 则称K(x,x′)是一个正定核函数。
其中 H 是Hilbert Space(完备的可能是无限维的被陚予内积的线性空间),如果去掉内积这个条件我们简单地称为核函数。
Hilbert空间定义:
⎩⎨⎧ 对称性: <f,g>=<g,f> 正定性: <f,f>≥0,"="⇔f=0 线性: ⟨r1f1+r2f2,g>=r1<f1,g>+r2<f2,g>
因为支持向量机的求解只用到内积运算,所以使用核函数会大大简化运算量。
四、正定核函数的证明
正定核函数还有另外一个定义:
如果核函数满足以下两条性质:
①对称性
②正定性
则称核函数K(x,z)为正定核函数。
这个定义也就是正定核函数的充要条件,其中两条性质分别指的是:
①对称性⇔K(x,z)=K(z,x);
②正定性⇔任取N个元素x1,x2,⋯,xN∈X,对应的GrammatrixK=[K(xi,xj)]是半正定的。
证明K(x,z)=ϕ(x)Tϕ(z)⇔对称性+矩阵K半正定:
①⇒:
首先证明对称性
K(x,z)=<ϕ(x),ϕ(z)>K(z,x)=<ϕ(z),ϕ(x)>又内积具有对称性,即<ϕ(x),ϕ(z)>=<ϕ(z),ϕ(x)>∴K(x,z)=K(z,x)∴K(x,z)满足对称性
然后证明
PS:先说明一下证明矩阵半正定的两种方法:
①特征值≥0
②∀α∈Rn,αTAα≥0
欲证Grammatrix:K=[K(xi,xj)]N×N半正定即证:∀α∈Rn,αTKα≥0∵αTK=(α1α2⋯αN)1×N⎣⎡a11a21⋮aN1a12a22⋮aN2⋯⋯⋱⋯a1Na2N⋮aNN⎦⎤N×N⎝⎛α1α2⋮αN⎠⎞N×1=i=1∑Nj=1∑NαiαjKij=i=1∑Nj=1∑Nαiαj<ϕ(xi),ϕ(xj)>=i=1∑Nj=1∑Nαiαjϕ(xi)Tϕ(xj)=i=1∑Nαiϕ(xi)Tj=1∑Nαjϕ(xj)=[∑i=1Nαiϕ(xi)]Tj=1∑Nαjϕ(xj)=<i=1∑Nαiϕ(xi),j=1∑Nαjϕ(xj)>=∥∥i=1∑Nαiϕ(xi)∥∥2≥0∴K是半正定的。
②⇐:
对K进⾏特征分解,对于对称矩阵K=VΛVT,那么令ϕ(xi)=λiVi,其中Vi是特征向量,于是就构造了K(x,z)=λiλjViTVj。
得证。
“开启掘金成长之旅!这是我参与「掘金日新计划 · 2 月更文挑战」的第 3 天,点击查看活动详情”