拉普拉斯变换是对傅立叶变换的推广，傅立叶变换要求 $e^{st}$ 中的s是一个纯虚数，而拉普拉斯推广到了复数。

拉普拉斯变换

拉普拉斯变换如下： $X(s)=\int_{-\infty}^\infty x(t)e^{-st}dt$

拉普拉斯和傅立叶的关系： $X(\sigma + j\omega)=\int_{-\infty}^\infty x(t)e^{(\sigma+j\omega)t}dt=\int_{-\infty}^\infty [x(t)e^{\sigma t}]e^{j\omega}dt$ ，拉普拉斯变换可以看作是对一个乘实指数信号后的傅立叶变换。

拉普拉斯变换需要同步给出 $s$ 的收敛域（Region of convergence, ROC）。这是因为会存在表达式一样但收敛域不同的情况，考虑下面的例子。

分别计算 $x(t)=e^{-at}u(t)$ 和 $y(t)=-e^{-at}u(-t)$ ，带入积分式可以发现，如果收敛那么 $X(s)=Y(s)=\frac{1}{s+a}$ ，但是收敛的域不一样，对于 $x(t)$ ，要求 $Re(s) < -a$ ，对于 $y(t)$ ，要求 $Re(s) > a$

remark: $e^{-at}u(t)$ 的拉普拉斯变换形式为 $\frac{1}{s+a}$ , ROC为 $Re(s)>-a$ ， $-e^{-at}u(-t)$ 的拉普拉斯变换形式为 $\frac{1}{s+a}$ , ROC为 $Re(s)<-a$

收敛域深入讨论

ROC具有以下特征

1 X(s)的ROC在s平面内是平行于虚轴的条带

这是因为收敛要求绝对可积，这个只对实部有约束
2 有理变换ROC内不包含极点。

所谓有理是指最后的变换完的形式是一个分式，分子和分母都是s的多项式。极点是分母多项式的0点。因为积分在极点处不收敛，所以ROC不会包含极点
3 x(t)有限持续期且绝对可积，那么ROC就是整个复平面

因为x(t)本身有限且绝对可积，那么不论你乘一个什么样的指数，其实都不会改变他的可积性，因此ROC不受拉普拉斯变换里那个s的影响。
4 x(t)为右边信号，并且如果某一个实部所对应的直线在ROC内，那么这个直线右侧全在ROC内。

所谓右边信号是指存在一个T，在小于T的位置信号都是0。在这种情况下，对于某个实部，如果拉普拉斯变换收敛了，那么更大的实部会让他衰减更快，更可以收敛。之所以要求是右边信号，就是因为衰减的快意味着左侧会更大，但因为左侧是有限的，所以不会影响可积性。
5 x(t)为左边信号，并且如果某一个实部所对应的直线在ROC内，那么这个直线左侧全在ROC内。

原理和上一条一样
6 x(t)为双边信号，并且如果某一个实部所对应的直线在ROC内，那么整个ROC应是包含该直线的条带。

结合上两条即可。把这个信号拆成一个左边信号和一个右边信号，那么ROC应该是两者的交集。而两者的ROC分别是向左和向右的半平面，因此求交集至多是一个条带。 3～6考虑了信号的所有情况，所以要么没有拉普拉斯变换，要么就是其中一种。
7 有理拉普拉斯的ROC的分界线总是落在极点上

结合2，4，5，可以知道，ROC内无极点，并且如果是左边信号，ROC是最左侧极点的左侧，右边信号，ROC是最右侧极点的右侧。

拉普拉斯逆变换

这个很好推，首先第一节已经发现，拉普拉斯变换 $X(\sigma + j\omega)$ 可以看作是对信号 $x(t)e^{-\sigma t}$ 的傅立叶变换，所以直接对 $X(\sigma + j\omega)$ 做傅立叶逆变换，得到的是 $x(t)e^{-\sigma t} =\frac{1}{2\pi} \int_{-\infty}^\infty X(\sigma + j\omega)e^{j\omega t}d\omega$ ，然后左边消去 $e^{-\sigma t}$ 把 $s=\sigma + j\omega$ 换元可得，

x(t)=\frac{1}{2\pi j}\int_{\sigma - j\infty}^{\sigma + j\infty}X(s)e^{st} ds

然而，对于有理变换，其实不需要直接求这个积分，因为可以直接把有理式拆分成一系列 $\frac{C}{s+a}$ 的形式，而这个由前面的remark可以直接恢复成 $\plusmn Ce^{-at}u(\plusmn t)$ 。然后根据ROC确定符号。

利用零极点图求 $X(s)$

一个有理变换可以整理成 $M\frac{\prod(s-\beta_i)}{\prod(s-a_j)}$ ，那么对于一个确定的s，可以在图上标出其位置，然后在实数轴标出 $a_j$ 的位置，此时从a指向s的向量就是 $s-a_j$ ，那么他的模就是长度（分母上是倒数），相位就是 $\plusmn\arctan$ 。如果是分子就是正号，分母就是负号。如果前面的系数M是复数，那么还要在增加一个 $\pi$

性质

基本和傅立叶一样，只是增加了ROC的讨论

线性： $ax(t)+by(t), L: aX(s)+bY(s)$ ，ROC求交集
时移： $x(t-t_0), L: e^{-st_0}X(s)$ ，ROC不变
s域移动：e^{s_0t}x(t), L: X(s-s_0) $,$ ROC=R+Re(s_0)$
伸缩： $x(at), L: \frac{1}{|a|}X(\frac{s}{a})$ , ROC=R/a
时间反转： $x(-t), L: X(-s)$ , ROC=-R
共轭： $x^*(t), L: X^*(s*)$ ，ROC不变
卷积： $x(t)*y(t), L: X(s)Y(s)$ , ROC求交，如果存在零极点相消，那么ROC可以更大
时域微分： $\frac{dx(t)}{dt}, L: sX(s)$ ，ROC包括R
s域微分： $dX(s)/ds, InverseL: -tx(t)$ ，ROC=R
时域积分： $\int_{-\infty}^t x(t)dt, L: \frac{1}{s}X(s)$ , ROC包括 $R\cap Re(s)>0$
初值与终值定理：前提条件 $t<0$ 时 $x(t)=0$ 并且 $x(t)$ 不包含冲激或高阶奇异导数，那么 $x(0^+)=\lim_{s\rightarrow \infty} sX(s)$ ， $\lim_{t\rightarrow \infty} x(t)=\lim_{s\rightarrow 0}sX(s)$

拉普拉斯与LTI

和傅立叶一样，如果单位冲激响应的拉普拉斯变换为 $H(s)$ ，那么对于 $y(t)=h(t)*x(t)$ ，有 $Y(s)=H(s)X(s)$ 。

因果系统的H的ROC是某个右半平面

这是因为因果系统的单位冲激响应只在t>0有，根据性质讨论可以得出此结论。如果是反过来结论不一定成立，但是如果H是有理的，那么因果性就等价于ROC位于最右侧极点的右边。
稳定系统等价于ROC包含虚数轴

因为稳定性要求h是绝对可积的，那么傅立叶变换收敛，这说明包含虚轴的ROC下H收敛。
推论：有理H的因果系统是稳定的，等价于所有极点都在左半平面

有理因果系统的ROC在最右侧极点的右边，所以如果所有极点都在左侧，他就包含虚轴

微分方程表征的系统

和傅立叶变换也基本一样

\sum_{k=0}^N a_k \frac{d^k y(t)}{dt^k} = \sum_{k=0}^N b_k \frac{d^k x(t)}{dt^k}

那么 $H(s)=\frac{\sum_{k=0}^M b_k s^k}{\sum_{k=0}^N a_k s^k}$

单边拉普拉斯变换

和双边唯一的区别是，积分下限从 $-\infty$ 变成了 $0^-$ 。

性质也几乎一样，区别点时间尺度变换a必须是正数，否则没意义，因此没有反转。此外时域微分： $\frac{dx(t)}{dt}, L: sX(s)-x(0^-)$ ，别的一样。

线性反馈系统

一个通用的反馈系统的系统框图如下图所示

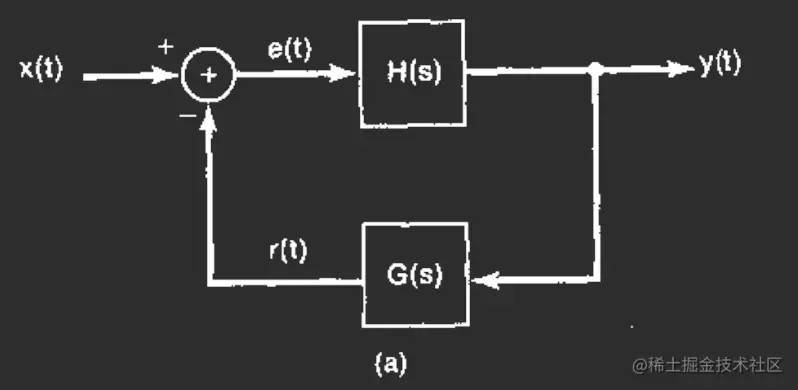从框图可以得到整个系统的系统函数 $Q(s)=\frac{H(s)}{1+G(s)H(s)}$

应用：构建逆系统

假设一个系统函数为 $P(s)$ ，那么构建 $G(s)=P(s), H(s)=K$ 的线性反馈系统，K足够大的时候，整体的系统函数近似为 $\frac{1}{P(s)}$ 。

应用2: 构建稳定系统

回顾第九章，稳定系统要求h绝对可积（保证输入有界的时候输出有界），对应其拉普拉斯变换的sROC包含虚轴，因此，考虑一个不稳定的系统 $H(s)=\frac{b}{s-a}$ ，然后设计一个 $G(s)=K$ ，反馈系统的拉普拉斯变换为 $Q(s)=\frac{b}{s-a+Kb}$ ，如果 $K>a//b$ ，ROC就包含虚轴了。

离散随机信号

有的时候信号可能不是确定的，而是一个随机过程的sample，这样需要考虑输入和输出就有变化。

考虑输入 $x[n]$ 是随机的，考虑信号在每个时刻的期望 $m_x[n] = E[x[n]]$ 。

广义平稳（WSS）的定义：一阶矩和二阶矩不随时间变化。

有了上述符号和平稳的概念，开始从定义出发分析。由定义：

y[n] = \sum_{k=-\infty}^\infty h[k] x[n-k]

两侧求期望，并按照期望的线性性有

m_y[n] = E[y[n]] = \sum_{k=-\infty}^\infty h[k] E[x[n-k]]

如果输入是平稳的，那么 $E[x[n]]=m_x$ ，所以

m_y[n] = \sum_{k=-\infty}^\infty h[k] m_x=m_x H(e^{j0})

这样可以看到，其实如果输入平稳，输出也是平稳的。

自相关函数 $\phi_{yy}[n,n+m]=E[y[n]y[n+m]]$ ，如果是平稳的，那么 $\phi_y[n,n+m]$ 只与间隔有关，可以简写为 $\phi_{yy}[m]$ 。

确定性自相关序列： $c_{hh}[l]=\sum_{k=-\infty}^\infty h[k]h[k+l]$ ，可以看作是 $h[n]*h[-n]$ ，假设h是实的，所以 $C_{hh}(e^{j\omega})=H(e^{j\omega})H^*(e^{j\omega})=|H(e^{j\omega})|^2$

如果用 $\Phi$ 表示 $\phi$ 的傅立叶变换，那么有 $\Phi_{yy}(e^{j\omega})=C_{hh}(e^{j\omega})\Phi_{xx}(e^{j\omega})$

$E[y^2[n]]=\phi_{yy}[0]=\frac{1}{2\pi}\int_{-\pi}^\pi \Phi_{yy}(e^{j\omega})d\omega= \frac{1}{2\pi}\int_{-\pi}^\pi |H(e^{j\omega})|^2 \Phi_{xx}(e^{j\omega})d\omega$

9 拉普拉斯