冲激串采样

一个周期冲激串可以表示为$p(t)=\sum_{k=-\infty}^\infty \delta(t-kT)$，假设原始信号为$x(t)$，那么经过采样的信号为$x_p(t)=x(t)p(t)$。

从频域上重新审视这个采样过程，$p(t)$经过傅立叶变换之后是$P(j\omega)=\frac{2\pi}{T}\sum_{k=-\infty}^\infty \delta(\omega-k\omega_s)$，其中$\omega_s=2\pi/T$为采样频率。这个计算参考第三章（周期信号的傅立叶级数系数推广过来）。

时域上相乘相当于频域上卷积，因此$X_p(j\omega)=\frac{1}{2\pi}P(j\omega) * X(j\omega)$。从第二章可以知道，$\delta(t-t_0)$函数卷积相当于做时移变换。这里形式相近，是一个频移，因此有$X_p(j\omega)=\frac{1}{T}\sum_{k=-\infty}^\infty X(j(\omega-k\omega_s))$

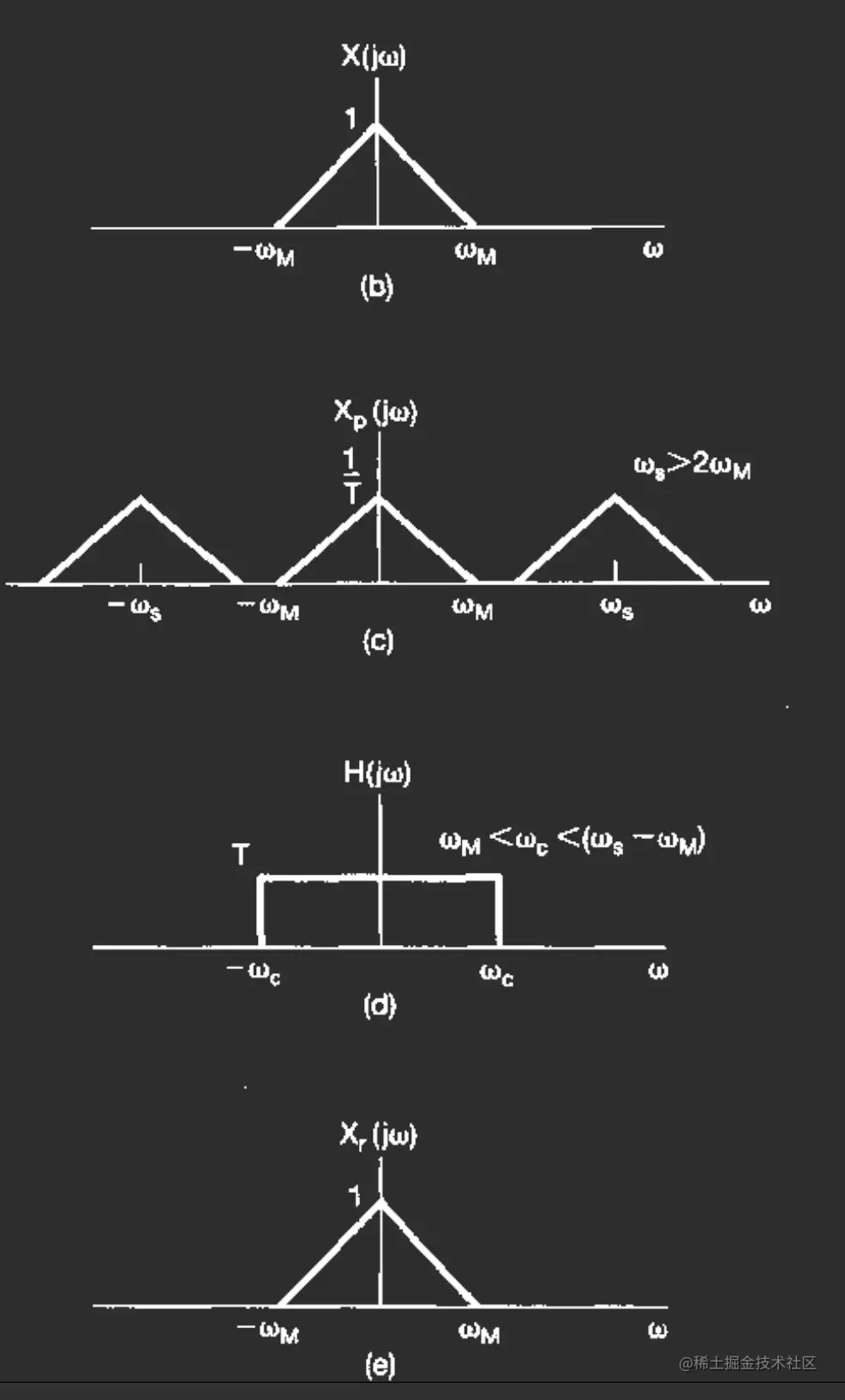
下面分析$X(j\omega)$的频率范围和采样频率之间的关系，如果$|\omega|\le \omega_M$，那么可以看到在$\omega_s > 2\omega_M$的情况下，采样信号的频率在不同的采样点出频率不会夹杂，那么利用低通滤波器（他的H是一个方波，刚好可以框住不重叠的一个X的频带）可以复原回来。

采样定理：如果$x(t)$有带限$|\omega|<\omega_M$，那么在$\omega_s>2\omega_M$的情况下，采样的信号$x_p$可以通过一个增益为T截止频率介于$\omega_M < \omega_c < \omega_s-\omega_M$的低通滤波器恢复出来。下面的图很好地说明了这个过程。

零阶保持采样

0阶保持其实是因为现实条件下不太容易实现，因此采样的信号很多时候是一个阶梯型的信号，即采样后的保持原值一直到下一次采样，这样的信号恢复起来就不是使用简单的低通滤波了。

考虑的思路是，零阶保持可以等效看作是冲激采样后再来一个保持的响应。如下图

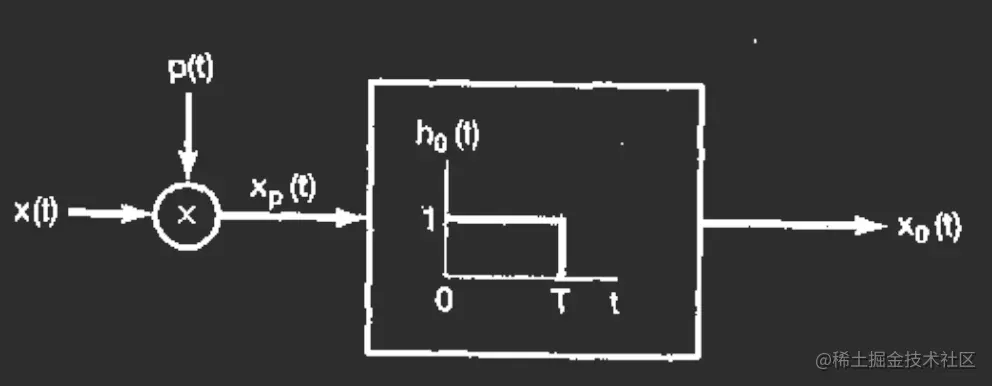那么对于这个单位冲激响应的傅立叶变换为$H_0(j\omega)=e^{-j\omega T}[\frac{2\sin(\omega T/2)}{\omega}]$

为了恢复这个信号，我们考虑在这个$x_0$后面接一个$h_r(t)$是他的输出就恢复成了$x(t)$，如果$h_r(t)$的傅立叶是$H_r(j\omega)$的，那么连接之后整体的响应就是$H_0(j\omega)H_r(j\omega)$，回顾前面冲激串采样，冲激串之后恢复采用了低通滤波$H(j\omega)$，而自从我们把0保持等效成了冲激串+$H_0$之后，就可以看到冲激串采样后面整体是$H_0(j\omega)H_r(j\omega)$，如果这个整体是$H(j\omega)$，那么就可以恢复，因此$H_r(j\omega)=\frac{H(j\omega)}{H_0(j\omega)}$

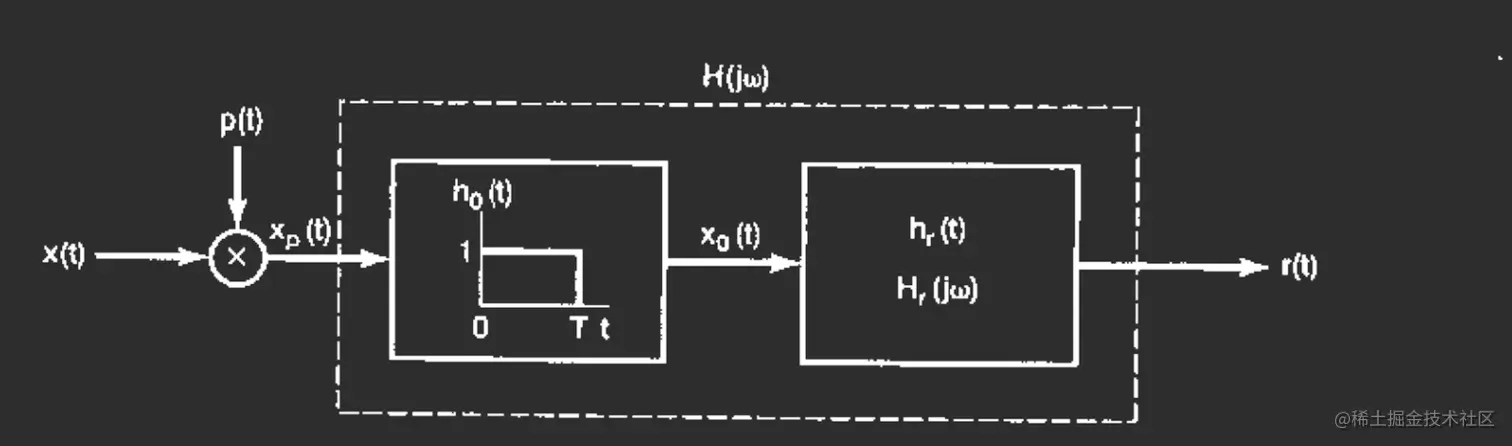
从另外一个视角看，如果我们有一系列的离散样本点，我们利用$H_0$，就可以得到一个对信号的零阶近似。

一阶内插

一阶内插的时域表示如下图

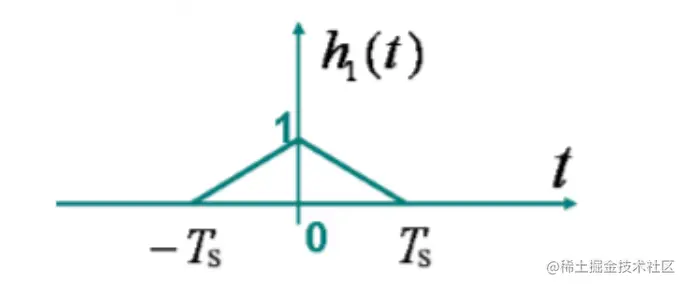他对应的傅立叶变换为$H_1(j\omega)=T_ssinc(\omega T_s/2)$

连续与离散结合

很多时候，把连续信号采样，作为离散信号内部处理，最后在输出成连续信号，是常见操作。 第一步叫C/D转换，第二步叫D/C转换。

先看第一步，假设输入信号$x(t)$，假设采样周期为$T$，那么采样信号为$x_p(t) = \sum_n x(nT)\delta(t-nT)$, 如果看作离散点，那么离散值为$x_d[n]=x(nT)$。

从频域角度看，因为$\delta(t-nT)$的傅立叶变换为$e^{-j\omega nT}$，因此$X_p(j\omega)=\sum_n x(nT)e^{-j\omega nT}$。而对于离散信号，其傅立叶变换为$X_d(e^{j\omega})=\sum_n x_d[n] e^{j\omega n}=\sum_n x(nT)e^{-j\omega n}$。因此，可以得到

而$X_p$的具体形式我们已知是$X_p(j\omega)=\frac{1}{T}\sum_{k=-\infty}^\infty X(j(\omega-k\omega_s))$，因此可以得到

这个的直观理解就是，$x_p$还是一个连续信号，所以他的间隔T你还能看出来，但离散信号间隔没有T了，所以除以T归一化。

D/C的过程很简单，可以利用增益为T的低通滤波实现 具体公式为

eg 数字微分器

设输入是连续信号$x_c(t)=\frac{\sin(\pi t/T)}{\pi T}$，系统的输出为$y_c(t)=\frac{dx_c(t)}{dt}$， 很明显，$y_c(t)=\frac{\cos(\pi t/T)}{Tt} - \frac{\sin(\pi t/T)}{\pi t^2}$。

如果是数字信号微分，首先需要采样转化成数字信号，这个信号的带限$\omega_M < \pi T$的，那么如果采样频率取$2\pi/T$，就足以保证采样定理避免混叠了。

确定采样周期为$T$后，需要考虑的是$x_c(t)$进入微分器会先变成$x_d[n]$，然后$x_d[n]$会变成$y_d[n]$在经过低通滤波恢复成$y_c(t)$，$x_d[n]==x_c(nT), y_d[n] = y_c(nT)$是很容易知道的，那么关键就在于，如何求出$h_d[n]$，使得$x_d[n]$能够变成$y_d[n]$。

我们发现$x_d[n] = x_c(nT)=\frac{1}{T}\delta[n]$，而$y_d[n]=y_c(nT)=\frac{(-1)^n}{nT^2}, (n \ne 0)$，那么根据变换的线性性，很容易得到$x_d[n]\rightarrow y_d[n]$的单位冲激响应$h_d[n]=\frac{(-1)^n}{nT}, (n \ne 0)$。

离散时间信号采样

设原始离散信号是$x[n]$，然后采样信号$p[n]=\sum_{k=-\infty}^\infty \delta[n-kN]$，就是每个N个点采样一个点。那么采样后的信号$x_p[n] = x[n]p[n]=\sum_{k=-\infty}^\infty x[kN]\delta[n-kN]$。

从频域角度上看,时域相乘等于频域卷积$X_p(e^{j\omega})=\frac{1}{2\pi}\int_{2\pi}P(e^{j\theta})X(e^{j(\omega-\theta)})d\theta$

而采样序列的傅立叶变换为$P(e^{j\omega})=\frac{2\pi}{N}\sum_{k=-\infty}^\infty \delta(\omega-k\omega_s)$，带入到前面的卷积运算里是$X_p(e^{j\omega})=\frac{1}{N}\sum_{k=0}^{N-1}X(e^{j(\omega-k\omega_s)})$

需要注意，这个信号的数量和原始信号一样，只不过中间的点数值为0而已。因此直接存储$x_p$很不划算，因为明明中间都是0，因此我们会使用抽取的方法，即令$x_b[n] = x_p[nN]=x[nN]$

这个抽取的信号和原始的采样信号有什么关系呢，还是在频域上分析。$X_b(e^{j\omega}) = \sum_k x_b[k]e^{-j\omega k}=\sum_k x_p[kN]e^{-j\omega k}=\sum_{n \% N=0}x_p[n]e^{-j\omega /N}=\sum_k x_p[n]e^{-j\omega n/N}=X_p(e^{j\omega/N})$

互补系统：离散信号的连续处理

输入信号为$x[n]$先转化成$x_c(t)$再经过处理变成$y_c(t)$，最后输出$y[n]$，那么从频域上$X_c(j\omega)=TX(e^{j\omega T})$, $Y_c(j\omega)=H_c(j\omega)X_c(j\omega)$, $Y(e^{j\omega})=\frac{1}{T}Y_c(j\omega/T)$，频率响应也有相同的关系$H(e^{j\omega})=H(j\omega/T)$, $H(e^{j\omega T})=H_c(j\omega)$