一、从线性回归到线性分类

1. 线性回归的特性

线性回归 $f(w, b)=w^T x+b$ 具备线性、全局性和数据末加工的特性。

线性包括三个方面，其中:

• 属性线性指的是 $f(w, b)$ 关于 $x$ 是线性的;
• 全局线性指的是 $w^T x+b$ 只是一个线性组合，然后直接就输出得到 $f(w, b)$ ；
• 系数线性指的是 $f(w, b)$ 关于 $w^T$ 是线性的。

全局性指的是线性回归是在整个特征空间上学习，并没有将特征空间进行划分然后在每个划分上学习。

数据未加工指的是线性回归直接在给定数据上进行学习没有对数据进行其他的加工。

其他的学习算法跟线性回归比较起来打破了其某些特性，在上面的树状图中也举出了一些例子。

2. 从线性回归到线性分类

线性回归经过一个激活函数然后根据一个阈值来获得分类的结果，如此就成为线性分类，也可以理解为将$w^{T}x+b$降维到一维而获得分类结果。

$$\begin{gathered} 激活函数 y=f\left(w^T x+b\right), y \in\left\{\begin{array}{c}\{0,1\}, \text { 硬分类 } \\ {[0,1], \text { 软分类 }}\end{array}\right.\\ 函数 f 叫做激活函数 (activation function)\\ 函数 f^{-1} 叫做链接函数 (link function)\\ f: w^T x+b \mapsto\{0,1\} /[0,1] \\ f^{-1}:\{0,1\} /[0,1] \mapsto w^T x+b \end{gathered}$$

3. 硬分类和软分类

二、感知机

两分类-硬分类-感知机算法

1. 概述

假设有一可以被线性分类的样本集 $\left\{\left(x_i, y_i\right)\right\}_{i=1}^N$ ，其中 $x_i \in \mathbb{R}^p, y_i\{-1,+1\}$ 。感知机算法（Perceptron Learning Algorithm）使用随机梯度下降法 (SGD) 来在特征空间 $\mathbb{R}^p$ 寻找一个超平面 $w^T x+b=0$ 来将数据 划分为正、负两类，其中 $w \in \mathbb{R}^p$ ，是超平面的法向量。 2. 学习策略 感知机的思想是错误驱动。其模型是 $f(x)=\operatorname{sign}\left(w^T x+b\right) ， f(x)$ 输出该样本点的类别，定义集合M为误分类点的集合。

补充：$w^T x$也可以表示$w^T x+b$，因为我们可以看做W = [W b] X = [X 1]^T

3. 可以确定对于误分类的数据 $\left(x_i, y_i\right)$ 来说，满足以下关系:

​ 损失函数的一个自然选择是误分类点的个数，即 $L(w)=\sum_{i=1}^N I\left\{-y_i\left(w^T x_i+b\right)>0\right\}$ ，但是这样的损失函数虽然直观，但是是非连续函数，所以不可导，不易优化。因此采用另一种损失函数，即误分类点到超平面的总距离。

在 $R^p$ 空间中任一点 $x_0$ 到超平面的距离为:

因此所有误分类点到超平面 $w^T x+b=0$ 的总距离为:

不考虑 $\frac{1}{\|w\|}$ ，就得到感知机的损失函数：

3. 学习算法 计算损失函数的梯度:

感知机的学习算法使用随机梯度下降法 (SGD)，这里选取 $\eta(0<\eta \leq 1)$ 作为学习率，其学习的步骤如下: ① 选取初值 $w_0, b_0$ ； ② 在训练集中选取数据 $\left(x_i, y_i\right)$ ； ③ 如果 $y_i\left(w^T x_i+b\right) \leq 0$ ，则更新参数：

④ 转至②，直到训练集中没有误分类点。 截止这里我们都是假设数据是线性可分的，如果线性不可分，可以用口袋算法 (pocket algorithm)，这里不做过多介绍。

三、线性判别分析

两分类-硬分类-线性判别分析 LDA

1. 概述

线性判别分析可用于处理二分类问题，其过程是寻找一个最佳的投影方向，使得样本点在该方向上的投影符合类内小、类间大的思想，具体指的是类内的方差之和小，类间的均值之差大。

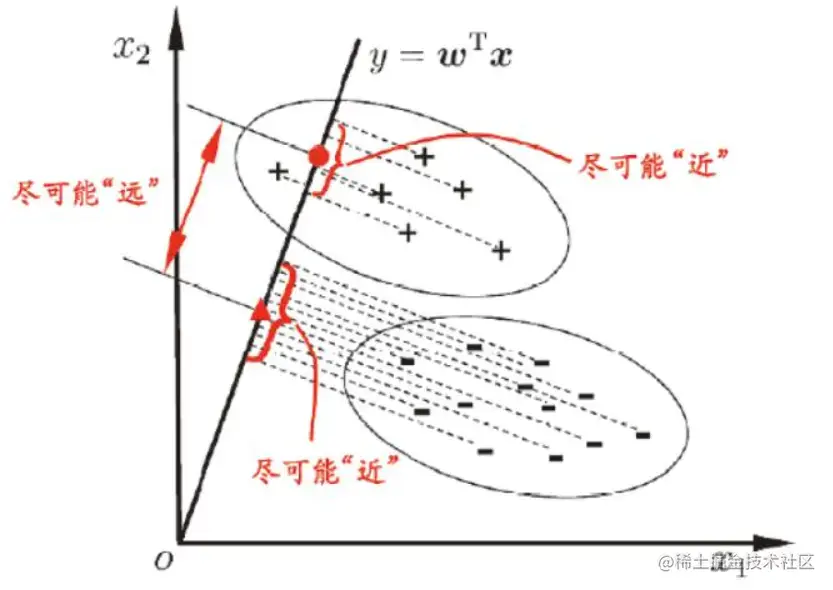
假设有以下数据：

$$\begin{gathered} X=\left(x_1, x_1, \cdots, x_N\right)^T=\left(\begin{array}{c} x_1^T \\ x_2^T \\ \vdots \\ x_N^T \end{array}\right)_{N \times p} Y=\left(\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array}\right)_{N \times 1} \\ \left\{\left(x_i, y_i\right)\right\}_{i=1}^N, x_i \in \mathbb{R}^p, y_i \in\left\{\frac{+1}{C_1} \frac{-1}{C_2}\right\} \\ x_{C_1}=\left\{x_i \mid y_i=+1\right\}, x_{C_2}=\left\{x_i \mid y_i=-1\right\} \\ \left|x_{C_1}\right|=N_1,\left|x_{C_2}\right|=N_2, N_1+N_2=N \end{gathered}$$

2. 线性判别分析的损失函数

投影轴的方向向量为 $w$ ，将样本点往该轴上投影以后的值 $z_i$ 为 $w^T x_i$ ，均值和方差按照如下方法计算:

均值 $\bar z=\frac{1}{N} \sum_{i=1}^N z_i=\frac{1}{N} \sum_{i=1}^N w^T x_i$

方差 $S_z=\frac{1}{N} \sum_{i=1}^N\left(w^T x_i-z^2\right)\left(w^T x_i-z^2\right)^T$

接下来计算每一类的均值和方差:

$$\begin{gathered} C_1: \\ \bar z_1=\frac{1}{N_1} \sum_{i=1}^{N_1} w^T x_i \\ S_1=\frac{1}{N_1} \sum_{i=1}^{N_1}\left(w^T x_i-\bar z_1\right)\left(w^T x_i-\bar z_1\right)^T \\ C_2: \\ \bar z_2=\frac{1}{N_2} \sum_{i=1}^{N_2} w^T x_i \\ S_2=\frac{1}{N_2} \sum_{i=1}^{N_2}\left(w^T x_i-\bar z_2\right)\left(w^T x_i-\bar z_2\right)^T \end{gathered}$$

类间：$\left(\bar z_1-\bar z_2\right)^2$

类内：$S_{1}+S_{2}$

定义损失函数:

$$\begin{gathered} J(w)=\frac{\left(\bar z_1-\bar z_2\right)^2}{S_1+S_2}\\ 分子=\left(\bar z_1-\bar z_2\right)^2=\left(\frac{1}{N_1} \sum_{i=1}^{N_1} w^T x_i-\frac{1}{N_2} \sum_{i=1}^{N_2} w^T x_i\right)^2 \\ =\left[w^T\left(\frac{1}{N_1} \sum_{i=1}^{N_1} x_i-\frac{1}{N_2} \sum_{i=1}^{N_2} x_i\right)\right]^2 \\ =\left[w^T\left(\bar x_{C_1}-\bar x_{C_2}\right)\right]^2 \\ =w^T\left(\bar x_{C_1}-\bar x_{C_2}\right)\left(\bar x_{C_1}-\bar x_{C_2}\right)^T w \\ --------------------\\ S_1=\frac{1}{N_1} \sum_{i=1}^{N_1}\left(w^T x_i-\bar z_1\right)\left(w^T x_i-\bar z_1\right)^T \\ =\frac{1}{N_1} \sum_{i=1}^{N_1}\left(w^T x_i-\frac{1}{N_1} \sum_{i=1}^{N_1} w^T x_i\right)\left(w^T x_i-\frac{1}{N_1} \sum_{i=1}^{N_1} w^T x_i\right)^T \\ =\frac{1}{N_1} \sum_{i=1}^{N_1} w^T\left(x_i-\bar x_{C_1}\right)\left(x_i-\bar x_{C_2}\right)^T w \\ =w^T\left[\frac{1}{N_1} \sum_{i=1}^{N_1}\left(x_i-\bar x_{C_1}\right)\left(x_i-\bar x_{C_2}\right)^T\right] w \\ =w^T S_{C_1} w \\ 分母=S_1+S_2=w^T S_{C_1} w+w^T S_{C_2} w=w^T\left(S_{C_1}+S_{C_2}\right) w \\ \therefore J(w)=\frac{w^T\left(\bar x_{C_1}-\bar x_{C_2}\right)\left(\bar x_{C_1}-\bar x_{C_2}\right)^T w}{w^T\left(S_{C_1}+S_{C_2}\right) w} \\ \end{gathered}$$

极大化 $J(w)$ 就可以使得类内的方差之和小，类间的均值之差大。

3. 线性判别分析的求解

$$\begin{gathered} & \text { 令 }\left\{\begin{array}{c} S_b=\left(\bar x_{C_1}-\bar x_{C_2}\right)\left(\bar x_{C_1}-\bar x_{C_2}\right)^T \\ S_w=S_{C_1}+S_{C_2} \end{array}\right. \\ & \text { 则 } J(w)=\frac{w^T S_b w}{w^T S_w w}=w^T S_b w\left(w^T S_w w\right)^{-1} \\ & \frac{\partial J(w)}{\partial w}=2 S_b w\left(w^T S_w w\right)^{-1}+w^T S_b w(-1)\left(w^T S_w w\right)^{-2} 2 S_b w \\ & =2\left[S_b w\left(w^T S_w w\right)^{-1}+w^T S_b w(-1)\left(w^T S_w w\right)^{-2} S_b w\right]=0 \\ & \left(w^T S_b w, w^T S_w w \in \mathbb{R}\right) \\ & \Rightarrow S_b w\left(w^T S_w w\right)-w^T S_b w S_w w=0 \\ & \Rightarrow w^T S_b w S_w w=S_b w\left(w^T S_w w\right) \\ & \Rightarrow S_w w=\frac{w^T S_w w}{w^T S_b w} S_b w \\ & \Rightarrow w=\frac{w^T S_w w}{w^T S_b w} S_w^{-1} S_b w \\ & \end{gathered}$$

(要注意对于 $w$ 我们只关注它的方向, 不关心它的大小。)

$$\begin{gathered} \Rightarrow w \propto S_w^{-1} S_b w \\ \Rightarrow w \propto S_w^{-1}\left(x_{C_1}^2-x_{C_2}^2\right) \underbrace{\left.x_{C_1}^2-x_{C_2}^2\right)^T w}_{1 \leqslant S_1} \\ \Rightarrow w \propto S_w^{-1}\left(x_{C_1}^2-x_{C_2}^2\right) \\ \Rightarrow w \propto\left(S_{C_1}+S_{C_2}\right)^{-1}\left(x_{C_1}^2-x_{C_2}^2\right) \end{gathered}$$

进一步如果 $S_w^{-1}$ 是各向同性的对角矩阵的话， $w \propto x_{C_1}^2-x_{C_2}^2$ 。

四、逻辑回归

两分类-软分类-概率判别模型-Logistic 回归

1. 概述

逻辑回归是一种二分类算法，通过 sigmoid 激活函数将线性组合 $w^T x$ 压缩到 0 和 1 之间来代表属于某一个分类的概率。 假设有如下数据：

2. sigmoid 激活函数

其图像为:

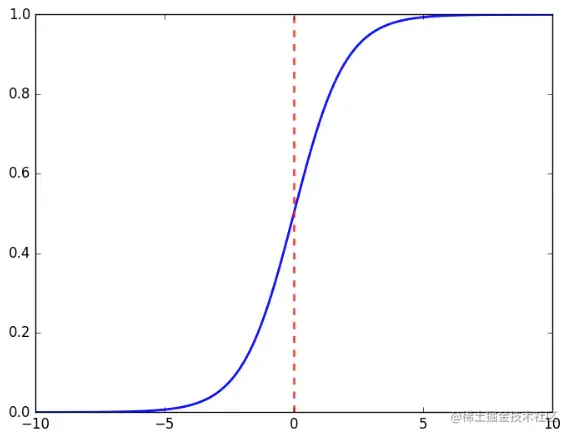
3. 逻辑回归的模型 逻辑回归预测 $y=1$ 的概率，然后根据极大似然估计法来求解。

4. 逻辑回归的求解

因此这里的极大似然估计就等价于极小化交叉熵损失函数。

求导的过程较为简单，就不做展示了。

五、高斯判别分析

两分类-软分类-概率生成模型-高斯判别分析 GDA

1. 概述

假设有如下数据：

2. 高斯判别分析的模型 在高斯判别分析中样本数据的类别 $y$ 在给定的情况下服从伯努利分布，另外不同类别中的样本数据分别服从多元高斯分布，因此有以下模型:

$$\begin{aligned} & \left.y \sim \text { Bernoulli }(\phi) \Leftrightarrow \begin{array}{c} \phi^y, y=1 \\ (1-\phi)^{1-y}, y=0 \end{array}\right\} P(y)=\phi^y (1 - \phi)^{1-y} \\ & \left.\begin{array}{l} x \mid y=1 \sim N\left(\mu_1, \Sigma\right) \\ x \mid y=0 \sim N\left(\mu_2, \Sigma\right) \end{array}\right\} P(x \mid y)=N\left(\mu_1, \Sigma\right)^y N\left(\mu_2, \Sigma\right)^{1-y} \\ & \end{aligned}$$

这里假设两个高斯分布具有同样的方差。 3. 高斯判别模型的求解

• 损失函数 高斯判别模型的损失函数为其 $\log$ 似然，要估计的参数 $\theta$ 为 $\left(\mu_1, \mu_2, \Sigma, \phi\right)$ :

$$L(\theta )=log\prod_{i=1}^{N}P(x_{i},y_{i})\\ =\sum _{i=1}^{N}logP(x_{i},y_{i})\\ =\sum _{i=1}^{N}logP(x_{i}|y_{i})P(y_{i})\\ =\sum _{i=1}^{N}[logP(x_{i}|y_{i})+logP(y_{i})]\\ =\sum _{i=1}^{N}[logN(\mu _{1},\Sigma )^{y_{i}}N(\mu _{2},\Sigma )^{1-y_{i}}+log\phi^{y_{i}}\phi^{1-y_{i}}]\\ =\sum _{i=1}^{N}[\underset{①}{\underbrace{logN(\mu _{1},\Sigma )^{y_{i}}}}+\underset{②}{\underbrace{logN(\mu _{2},\Sigma )^{1-y_{i}}}}+\underset{③}{\underbrace{log\phi^{y_{i}}\phi^{1-y_{i}}}}]$$

然后使用极大似然估计法来求解：

$$\hat{\theta }=\underset{\theta}{argmax}L(\theta )$$

定义标签为$1$的样本个数为$N_{1}$，标签为$0$的样本个数为$N_{2}$，则有$N_{1}+N_{2} = N$。

• 求解$\phi$

$\phi$只存在于③式中，因此求解$\phi$只需要看③式即可：

$$③=\sum _{i=1}^{N}[y_{i}log\phi +(1-y_{i})log(1-\phi )]\\ \frac{\partial ③}{\partial \phi}=\sum _{i=1}^{N}[y_{i}\frac{1}{\phi}-(1-y_{i})\frac{1}{1-\phi }]=0\\ \Rightarrow \sum _{i=1}^{N}[y_{i}(1-\phi)-(1-y_{i})\phi ]=0\\ \Rightarrow \sum _{i=1}^{N}(y_{i}-\phi)=0\\ \Rightarrow \sum _{i=1}^{N}y_{i}-N\phi=0\\ \hat{\phi}=\frac{1}{N}\sum _{i=1}^{N}y_{i}=\frac{N_{1}}{N}$$

• 求解$\mu_{1}、\mu_{2}$

$\phi$只存在于①式中，因此求解$\mu_{1}$只需要看①式即可：

$$①=\sum _{i=1}^{N}y_{i}log\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}exp\left \{-\frac{1}{2}(x_{i}-\mu _{1})^{T}\Sigma ^{-1}(x_{i}-\mu _{1})\right \}\\ \mu _{1}=\underset{\mu _{1}}{argmax}①\\ =\underset{\mu _{1}}{argmax}\sum _{i=1}^{N}y_{i}[log\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}-\frac{1}{2}(x_{i}-\mu _{1})^{T}\Sigma ^{-1}(x_{i}-\mu _{1})]\\ =\underset{\mu _{1}}{argmax}\sum _{i=1}^{N}y_{i}[-\frac{1}{2}(x_{i}-\mu _{1})^{T}\Sigma ^{-1}(x_{i}-\mu _{1})]\\ =\underset{\mu _{1}}{argmax}\Delta\\ \Delta=\sum _{i=1}^{N}y_{i}[-\frac{1}{2}(x_{i}-\mu _{1})^{T}\Sigma ^{-1}(x_{i}-\mu _{1})]\\ =-\frac{1}{2}\sum _{i=1}^{N}y_{i}(x_{i}^{T}\Sigma ^{-1}-\mu _{1}^{T}\Sigma ^{-1})(x_{i}-\mu _{1})\\ =-\frac{1}{2}\sum _{i=1}^{N}y_{i}(x_{i}^{T}\Sigma ^{-1}x_{i}-2\mu _{1}^{T}\Sigma ^{-1}x_{i}+\mu _{1}^{T}\Sigma ^{-1}\mu _{1})\\ \frac{\partial \Delta}{\partial \mu _{1}}=-\frac{1}{2}\sum _{i=1}^{N}y_{i}(-2\Sigma ^{-1}x_{i}+2\Sigma ^{-1}\mu _{1})=0\\ \Rightarrow \sum _{i=1}^{N}y_{i}(\Sigma ^{-1}\mu _{1}-\Sigma ^{-1}x_{i})=0\\ \Rightarrow \sum _{i=1}^{N}y_{i}(\mu _{1}-x_{i})=0\\ \Rightarrow \sum _{i=1}^{N}y_{i}\mu _{1}=\sum _{i=1}^{N}y_{i}x_{i}\\ \hat{\mu _{1}}=\frac{\sum _{i=1}^{N}y_{i}x_{i}}{\sum _{i=1}^{N}y_{i}}=\frac{\sum _{i=1}^{N}y_{i}x_{i}}{N_{1}}\\ 同理\hat{\mu _{2}}=\frac{\sum _{i=1}^{N}y_{i}x_{i}}{N_{2}}$$

• 求解$\Sigma$

以下是求解过程中用到的一些预备知识：

$$\frac{\partial tr(AB)}{\partial A}=B^{T} \\ \frac{\partial |A|}{\partial A}=|A|A^{-1} \\ tr(AB)=tr(BA)\\ tr(ABC)=tr(CAB)=tr(BCA)$$

两类数据按照以下两个集合来表示：

$$C_{1}=\left \{x_{i}|y_{i}=1,i=1,2,\cdots ,N\right \}\\ C_{2}=\left \{x_{i}|y_{i}=0,i=1,2,\cdots ,N\right \}\\ |C_{1}|=N_{1},|C_{2}|=N_{2},N_{1}+N_{2}=N$$

然后进行求解：

$$\hat{\Sigma }=\underset{\Sigma }{argmax}(①+②)\\ ①+②=\sum _{x_{i}\in C_{1}}logN(\mu _{1},\Sigma )+\sum _{x_{i}\in C_{2}}logN(\mu _{2},\Sigma )$$

然后求解上式中的通项：

$\sum_{i=1}^{N}logN(\mu ,\Sigma )=\sum_{i=1}^{N}log\frac{1}{(2\pi )^{p/2}|\Sigma |^{1/2}}exp\left \{-\frac{1}{2}(x_{i}-\mu )^{T}\Sigma ^{-1}(x_{i}-\mu )\right \}\\ =\sum_{i=1}^{N}[log\frac{1}{(2\pi )^{p/2}}+log|\Sigma |^{-\frac{1}{2}}-\frac{1}{2}(x_{i}-\mu )^{T}\Sigma ^{-1}(x_{i}-\mu )]\\ =\sum_{i=1}^{N}[C-\frac{1}{2}log|\Sigma |-\frac{1}{2}(x_{i}-\mu )^{T}\Sigma ^{-1}(x_{i}-\mu )]\\ =C-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}\sum_{i=1}^{N}(x_{i}-\mu )^{T}\Sigma ^{-1}(x_{i}-\mu )\\ =C-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}\sum_{i=1}^{N}tr[(x_{i}-\mu )^{T}\Sigma ^{-1}(x_{i}-\mu )]\\ (实数的迹等于其本身)\\ =C-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}\sum_{i=1}^{N}tr[(x_{i}-\mu )(x_{i}-\mu )^{T}\Sigma ^{-1}]\\ =C-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}tr[\sum_{i=1}^{N}(x_{i}-\mu )(x_{i}-\mu )^{T}\Sigma ^{-1}]\\ =C-\frac{1}{2}tr(NS\Sigma ^{-1})\\ (S=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-\mu )(x_{i}-\mu )^{T},为协方差矩阵)\\ =-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}Ntr(S\Sigma ^{-1})+C\\ 则①+②=-\frac{1}{2}N_{1}log|\Sigma |-\frac{1}{2}N_{1}tr(S_{1}\Sigma ^{-1})-\frac{1}{2}N_{2}log|\Sigma |-\frac{1}{2}N_{2}tr(S_{2}\Sigma ^{-1})+C\\ =-\frac{1}{2}Nlog|\Sigma |-\frac{1}{2}N_{1}tr(S_{1}\Sigma ^{-1})-\frac{1}{2}N_{2}tr(S_{2}\Sigma ^{-1})+C\\ =-\frac{1}{2}[Nlog|\Sigma |+N_{1}tr(S_{1}\Sigma ^{-1})+N_{2}tr(S_{2}\Sigma ^{-1})]+C$

然后对$\Sigma$进行求导：

$$\frac{\partial ①+②}{\partial \Sigma}=-\frac{1}{2}[N\frac{1}{|\Sigma |}|\Sigma |\Sigma^{-1}+N_{1}\frac{\partial tr(\Sigma ^{-1}S_{1})}{\partial \Sigma}+N_{2}\frac{\partial tr(\Sigma ^{-1}S_{2})}{\partial \Sigma}]\\ =-\frac{1}{2}[N\Sigma^{-1}+N_{1}S_{1}^{T}(-1)\Sigma ^{-2}+N_{2}S_{2}^{T}(-1)\Sigma ^{-2}]\\ =-\frac{1}{2}(N\Sigma^{-1}-N_{1}S_{1}^{T}\Sigma ^{-2}-N_{2}S_{2}^{T}\Sigma ^{-2})\\ =0\\ N\Sigma-N_{1}S_{1}-N_{2}S_{2}=0\\ \hat{\Sigma}=\frac{N_{1}S_{1}+N_{2}S_{2}}{N}$$

六、朴素贝叶斯

两分类-软分类-概率生成模型-朴素贝叶斯

1. 概述

假设有如下数据：

$$\left \{(x_{i},y_{i})\right \}_{i=1}^{N},x_{i}\in \mathbb{R}^{p},y_{i}\in \left \{0,1\right \}$$

1. 朴素贝叶斯的模型

朴素贝叶斯分类器可以用来做多分类，其基本思想是条件独立性假设，即假设数据的每个特征之间是相互独立的，其形式化表达为

$$对于x|y来说x^{i}|y与x^{j}|y是相互独立的（i\neq j），即\\ P(x|y)=\prod_{i=1}^{p}P(x^{i}|y)$$

朴素贝叶斯分类器是最简单的概率图模型（有向图）:

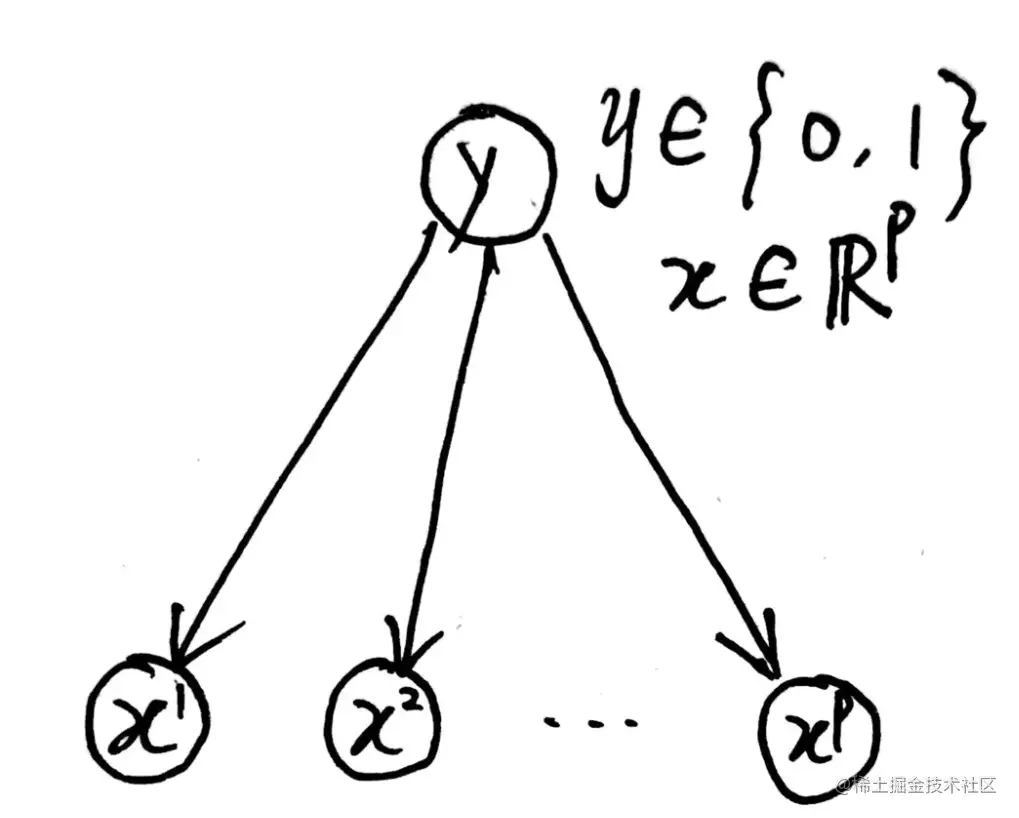
给定$x$，判断$y$的类别可以通过以下方法，即将$x$归为类别的概率中最大的一类：

$$\hat{y}=\underset{y}{argmax}P(y|x)\\ =\underset{y}{argmax}\frac{P(x,y)}{P(x)} \\ =\underset{y}{argmax}\frac{P(y)P(x|y)}{P(x)} \\ =\underset{y}{argmax}P(y)P(x|y)$$

$P(y)$是先验概率，如果有两类则服从伯努利分布（Bernoulli distribution），如果有多类则服从类别分布（Categorical distribution）。$P(x|y)$则符合条件独立性假设$P(x|y)=\prod_{i=1}^{p}P(x^{i}|y)$，其中对于$x^{i}$，如果$x^{i}$是离散的，则可以认为其服从类别分布（Categorical distribution），如果$x^{i}$是连续的，则可以认为其服从高斯分布（Gaussian distribution)。

至于其求解过程则可以根据具体情况使用极大似然估计法即可。对于朴素贝叶斯方法重要的是理解其条件独立性假设，这个假设也是其被称为“朴素（Naive）”的原因。

七、小结

分类任务分为两类，对于需要直接输出类别的任务，感知机算法中我们在线性模型的基础上加入符号函数作为激活函数，那么就能得到这个类别，但是符号函数不光滑，于是我们采用错误驱动的方式，引入 $\sum\limits_{x_i\in\mathcal{D}_{wrong}}-y_iw^Tx_i$ 作为损失函数，然后最小化这个误差，采用批量随机梯度下降的方法来获取最佳的参数值。而在线性判别分析中，我们将线性模型看作是数据点在某一个方向的投影，采用类内小，类间大的思路来定义损失函数，其中类内小定义为两类数据的方差之和，类间大定义为两类数据中心点的间距，对损失函数求导得到参数的方向，这个方向就是 $S_w^{-1}(\overline x_{c1}-\overline x_{c2})$，其中 $S_w$ 为原数据集两类的方差之和。

另一种任务是输出分类的概率，对于概率模型，我们有两种方案，第一种是判别模型，也就是直接对类别的条件概率建模，将线性模型套入 Logistic 函数中，我们就得到了 Logistic 回归模型，这里的概率解释是两类的联合概率比值的对数是线性的，我们定义的损失函数是交叉熵（等价于 MLE），对这个函数求导得到 $\frac{1}{N}\sum\limits_{i=1}^N(y_i-p_1)x_i$，同样利用批量随机梯度（上升）的方法进行优化。第二种是生成模型，生成模型引入了类别的先验，在高斯判别分析中，我们对数据集的数据分布作出了假设，其中类先验是二项分布，而每一类的似然是高斯分布，对这个联合分布的对数似然进行最大化就得到了参数， $\frac{\sum\limits_{i=1}^Ny_ix_i}{N_1},\frac{\sum\limits_{i=1}^N(1-y_i)x_i}{N_0},\frac{N_1S_1+N_2S_2}{N},\frac{N_1}{N}$。在朴素贝叶斯中，我们进一步对属性的各个维度之间的依赖关系作出假设，条件独立性假设大大减少了数据量的需求。