Vue3源码分析(11)-最长递增子序列diff算法

本文介绍

• 之前我们详细讲解了patch函数,但是文章结尾有两个重要的函数还没有剖析。他们分别是patchUnkeyedChilren和patchKeyedChildren,其中patchKeyedChildren就是最难理解的diff算法。
• 本文我们会先详细介绍diff算法的流程。然后再详细剖析patchUnkeyedChildren函数。

最长递增子序列diff算法

• c1:之前的children属性。
• c2:当前最新的children属性。
• e1:c1数组的最后一个值的索引。
• e2:c2数组的最后一个值的索引。
• isSameVNode:判断两个vnode是否相同。

function isSameVNode(n1,n2){
  return n1.type === n2.type && n1.key === n2.key
}

1.头比较

let i = 0;//遍历的索引值
const l2 = c2.length;
let e1 = c1.length - 1;
let e2 = l2 - 1;

• 先进行一些初始化操作。

while (i <= e1 && i <= e2) {
  const n1 = c1[i];
  const n2 = (c2[i] = normalizeVNode(c2[i]));
  //找出相同节点patch
  if (isSameVNodeType(n1, n2)) {
    patch(
      n1,
      n2,
      container,
      null,
    );
  } else {
    //不同节点退出循环
    break;
  }
  i++;//向前移动指针
}

• n1:当前被比较的vnode。
• n2:当前比较的vnode。
• 从头部开始一一比较,找到哪些节点是相同的,找到的节点表示不需要发生任何移动。调用patch函数更新即可。直到发现当前比较的n1、n2不相同,退出循环。

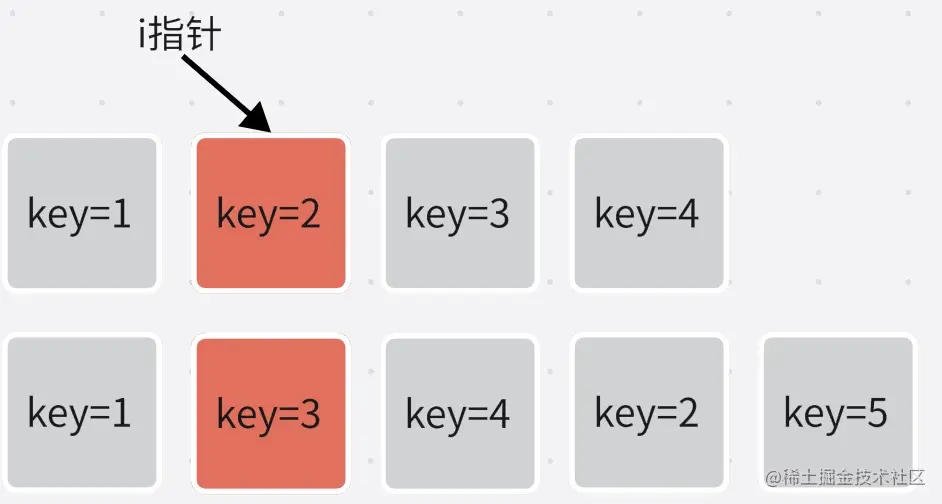
2.尾比较

while (i <= e1 && i <= e2) {
  const n1 = c1[e1];
  const n2 = (c2[e2] = normalizeVNode(c2[e2]));
  //找到相同的节点patch
  if (isSameVNodeType(n1, n2)) {
    patch(
      n1,
      n2,
      container,
      null,
    );
  } else {
    //不相同则退出循环
    break;
  }
  e1--;//向前移动指针
  e2--;//向前移动指针
}

• 排除掉不需要移动的尾节点。

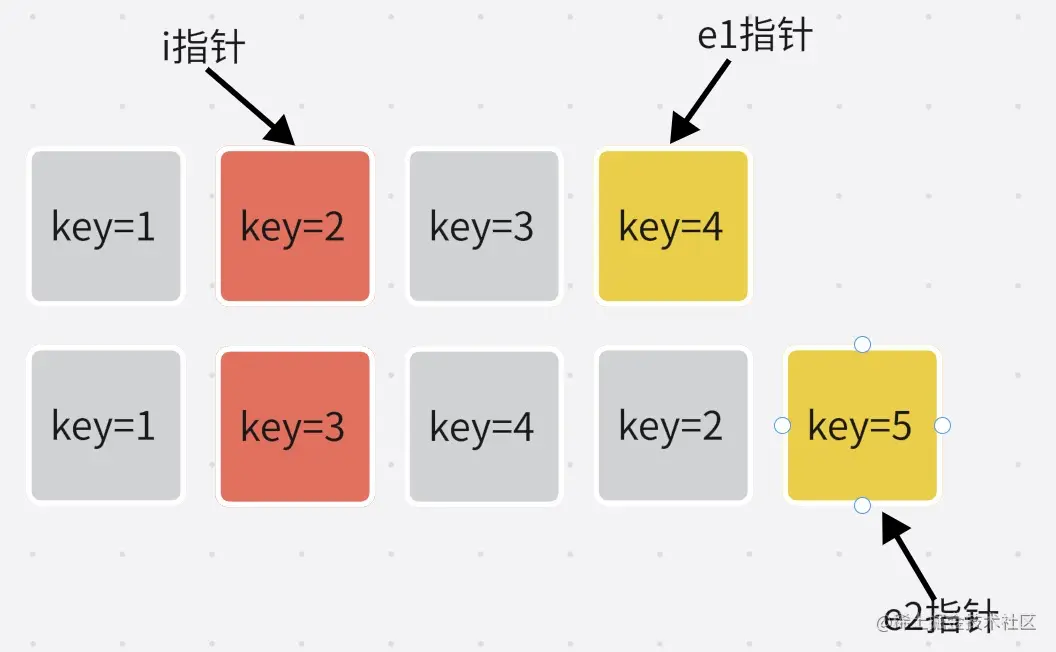
3.新增节点

if (i > e1) {
  if (i <= e2) {
    const nextPos = e2 + 1;
    const anchor = nextPos < l2 ? c2[nextPos].el : parentAnchor;
    while (i <= e2) {
      patch(
        null,
        (c2[i] = normalizeVNode(c2[i])),
        container,
        anchor,
      );
      i++;
    }
  }
}

• i>e1:之前通过尾比较和头比较,如果i>e1表示c1已经遍历完毕。
• i<=e2:表示c2还没有遍历完毕,这说明有新增的节点。
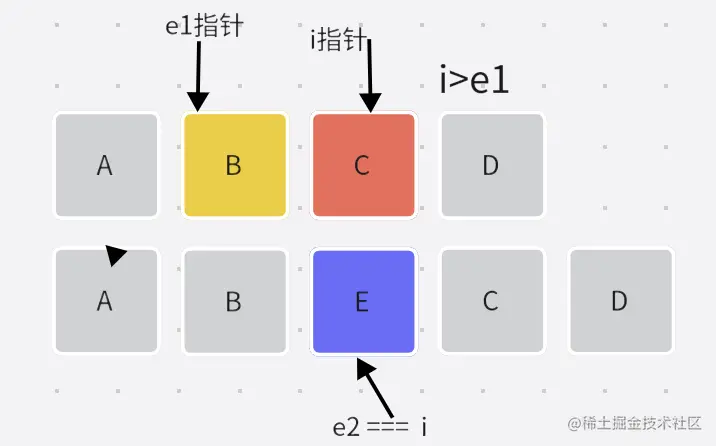
• 根据图像可以发现新增的节点就是[i,e2]中所有的节点。

4.删除节点

if(i>e1){}
else if (i > e2) {
  while (i <= e1) {
    unmount(c1[i], parentComponent, parentSuspense, true);
    i++;
  }
}

• c1未遍历完但是c2遍历完了表示有需要删除的节点。
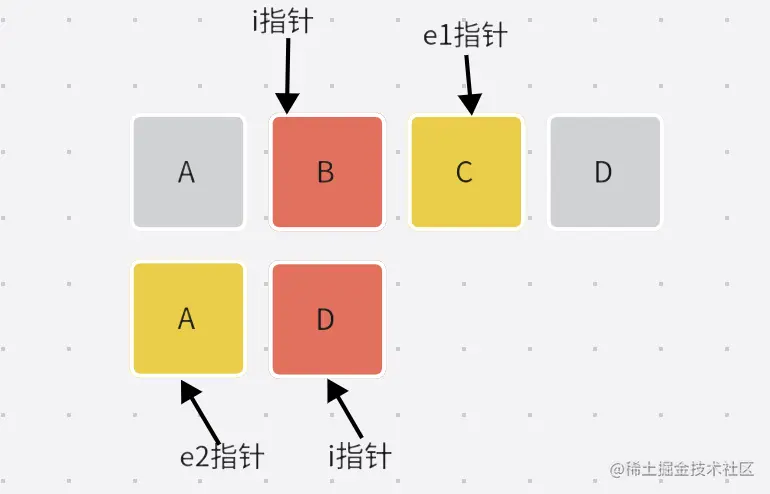
• 可以发现[i,e1]的所有节点需要被删除。

5.处理特殊情况

1. 构建keyToNewIndexMap表。

const s1 = i;//设置s1 s2初始值
const s2 = i;
//创建映射表用于快读通过节点的key找到
//这个节点在c2中的位置
const keyToNewIndexMap = new Map();
for (i = s2; i <= e2; i++) {
  const nextChild = (c2[i] = optimized
    ? cloneIfMounted(c2[i])
    : normalizeVNode(c2[i]));
  if (nextChild.key != null) {
    //如果有相同的key需要报错
    if (keyToNewIndexMap.has(nextChild.key)) {
      warn(
        `Duplicate keys found during update:`,
        JSON.stringify(nextChild.key),
        `Make sure keys are unique.`
      );
    }
    //将key作为键 c2中这个节点的索引作为值
    keyToNewIndexMap.set(nextChild.key, i);
  }
}

• 我们可以通过这个例子来理解这个表的作用。

//防止前面四步的干扰,这个序列不会进入前四个分支
c1:A B C D E //当前DOM顺序
c2:E D C B A //通过diff算法变换后顺序
keyToNewIndexMap = {
  E:0,
  D:1,
  C:2,
  B:3,
  A:4
}

• 这里的表是通过c2构建的,通过这个表可以快速找到c2中vnode的位置。例如c1中的A节点,通过keyToNewIndexMap可以快速知道A节点在c2中的位置为4。
• 如果c1中的某个节点无法在keyToNewIndexMap中找到代表这个节点需要被删除。
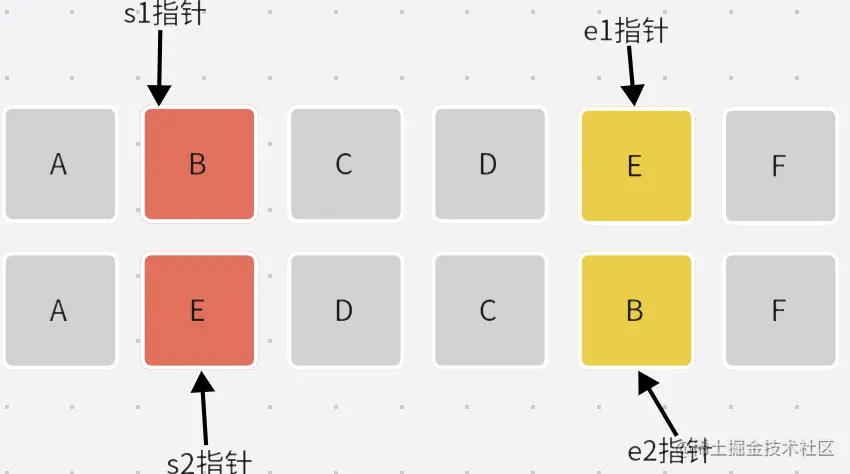
• 下面给出了s1、s2、e1、e2分别代表什么。

2. 创建newIndexToOldIndexMap数组,这个数组的长度为e2-s2+1,初始值都为0。

let j;
let patched = 0;//已经比较过的节点数量
//应该被比较的节点数量
const toBePatched = e2 - s2 + 1;
let moved = false;//是否存在需要移动的节点
let maxNewIndexSoFar = 0;
const newIndexToOldIndexMap = new Array(toBePatched);
for (i = 0; i < toBePatched; i++) newIndexToOldIndexMap[i] = 0;

• toBePatched:c2中应该被patch的数量。
• patched:已经被patch过的数量。
• newIndexToOldIndexMap:用于找到哪些节点需要被移动。

3. 遍历[s1,e1]中所有节点,找到每个节点在c2中的位置。并完成newIndexToOldIndexMap的赋值。

for (i = s1; i <= e1; i++) {
  //获取c1中当前需要比较的节点。
  const prevChild = c1[i];
  //如果已经patch过的数量大于应该patched的数量
  //表示有节点需要被删除。
  if (patched >= toBePatched) {
    unmount(prevChild, parentComponent, parentSuspense, true);
    continue;
  }
  let newIndex;
  if (prevChild.key != null) {
    //根据prevChild的key找到这个节点在
    //c2中的索引
    newIndex = keyToNewIndexMap.get(prevChild.key);
  } else {
    //不考虑这里的情况
  }
  //如果没有找到则卸载这个节点
  if (newIndex === undefined) {
    unmount(prevChild, parentComponent, parentSuspense, true);
  } else {
    //建立同一个元素在c1和c2中位置的关系
    newIndexToOldIndexMap[newIndex - s2] = i + 1;
    //判断是否需要移动
    if (newIndex >= maxNewIndexSoFar) {
      maxNewIndexSoFar = newIndex;
    } else {
      //标识当前有元素是需要移动的
      moved = true;
    }
    //更新节点
    patch(
      prevChild,
      c2[newIndex],
      container,
      null,
    );
    //已经完成一次比较,patched的值加1
    patched++;
  }
}

• 首先判断当前是否有需要卸载的节点,如果有则卸载。
• 根据prevChild找到这个节点在c2中的位置索引,如果找不到应该卸载当前节点。
• i表示的是c1中当前节点的位置,newIndex表示的是c2中当前节点的位置,给他们建立联系。
• newIndexToOldIndexMap: 数组的索引与c2中需要比较的节点一一对应,数组的每一个值表示的是当前节点在c1中的位置索引+1。
• maxNewIndexSoFar:maxNewIndexSoFar代表上一次的newIndex,如果当前的newIndex小于了上一次的newIndex,这表示在c1中上一个节点在当前节点的前面,但是在c2中上一个节点在当前节点后面,代表节点的位置发生了移动,所以需要设置moved=true。
• 我们再来看看图解。
• 第一次循环:
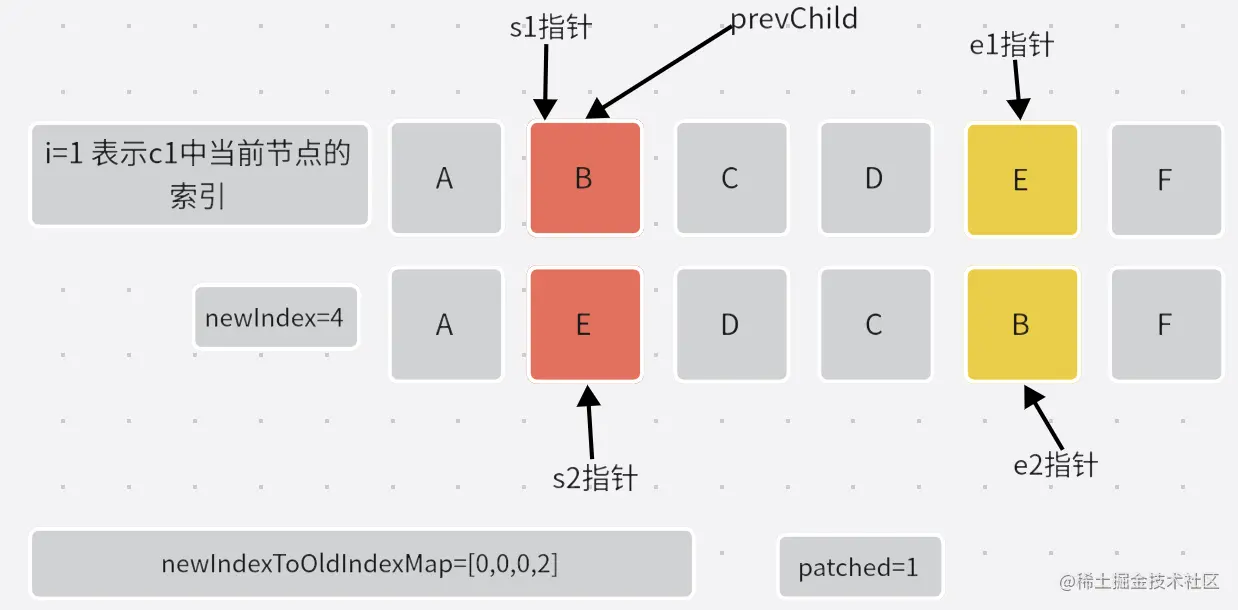
• 第二次循环:
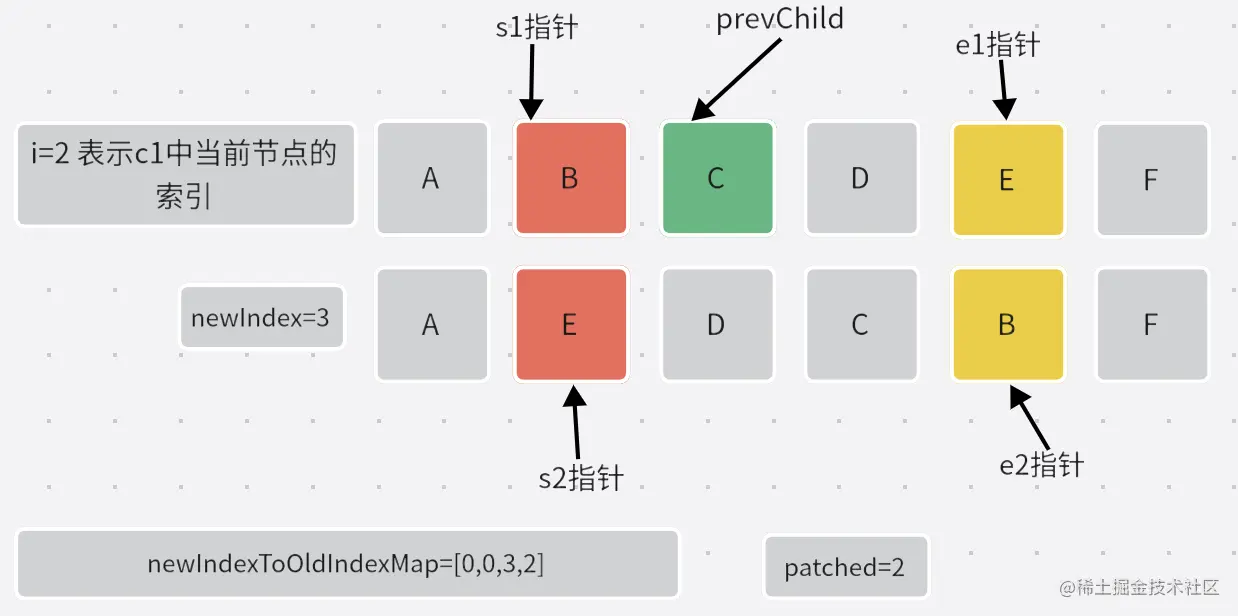
• 第三次循环:
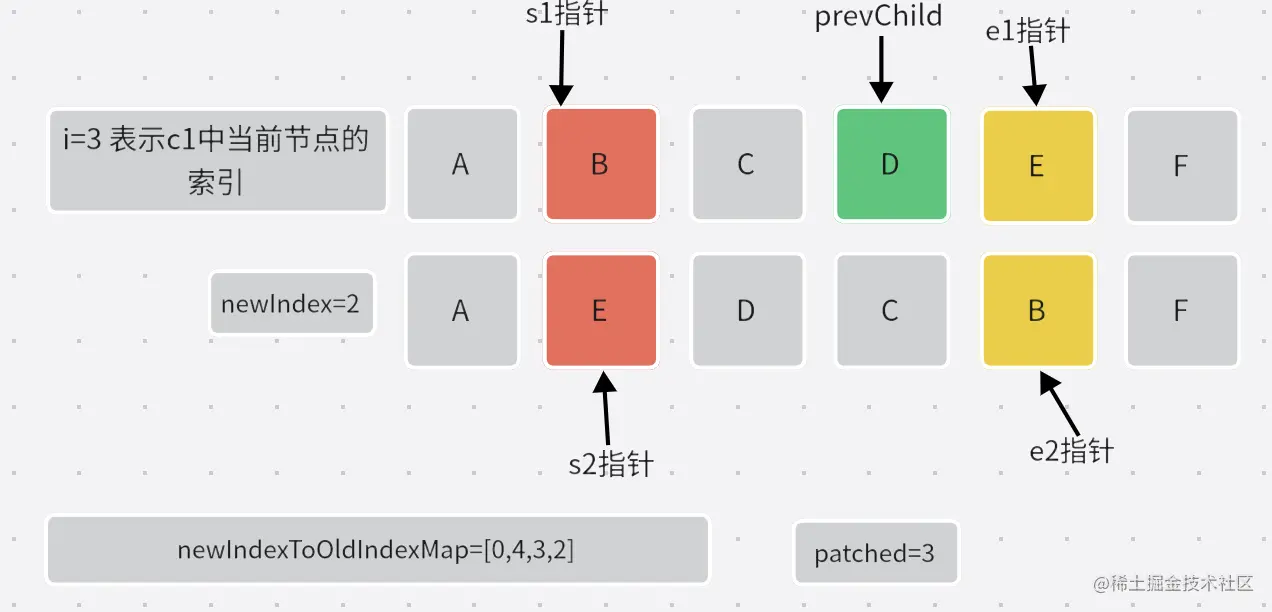
• 第四次循环:
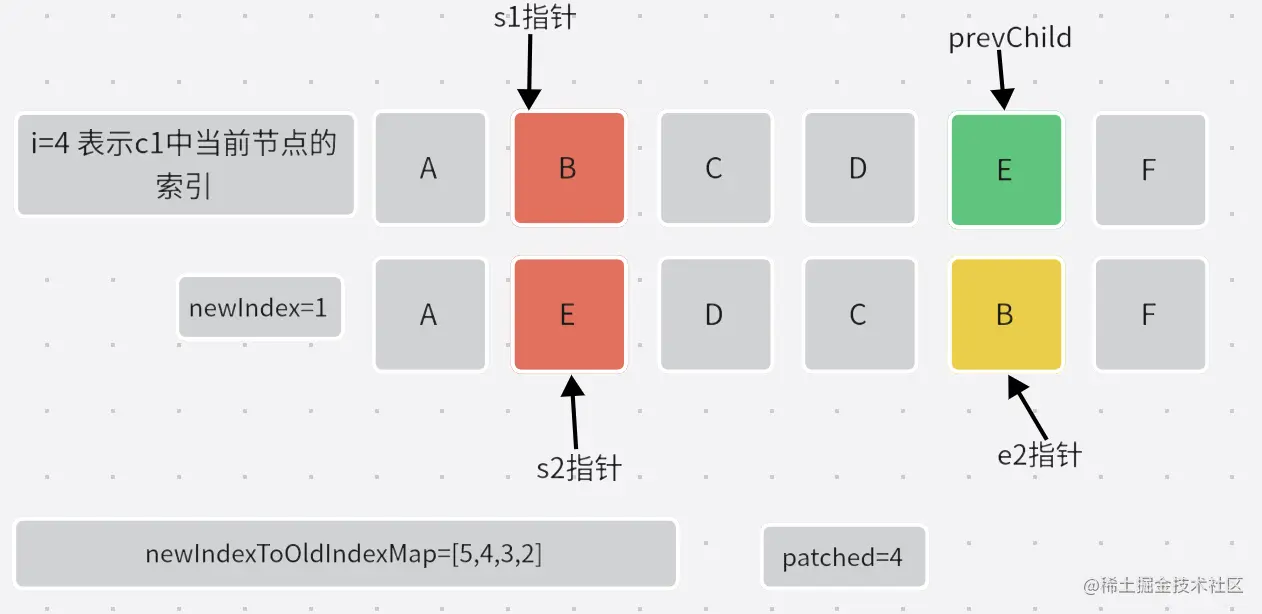
• 最终得到的newIndexToOldIndexMap=[5,4,3,2]。其中newIndexToOldIndexMap[n]===m代表 在c2索引为n+s2的位置的节点应该为c1中索引为n-1的位置。例如(n=0 m=5)代表在c2中第二个节点应该为c1中的第五个节点、(n=1 m=4)代表在c2中第三个节点应该为c1中的第四个节点。

4. 获取最长递增子序列并移动节点。

//获取newIndexToOldIndexMap中最长
//递增子序列的索引数组
const increasingNewIndexSequence = moved
  ? getSequence(newIndexToOldIndexMap)
  : shared.EMPTY_ARR;
//获取最长递增子序列数组的最后一个索引
j = increasingNewIndexSequence.length - 1;
//在[s2,e2]范围内重后向前遍历
for (i = toBePatched - 1; i >= 0; i--) {
  const nextIndex = s2 + i;//还原e2在c2中的实际位置
  const nextChild = c2[nextIndex];//获取这个child
  //获取节点需要插入的位置
  const anchor = nextIndex + 1 < l2 ? c2[nextIndex + 1].el : parentAnchor;
  //如果在newIndexToOldIndexMap中为0表示需要新增
  if (newIndexToOldIndexMap[i] === 0) {
    patch(
      null,
      nextChild,
      container,
      anchor,
    );
  } 
  //需要移动
  else if (moved) {
    //j<0表示最长递增子序列遍历完了,后续的节点都需要插入
    //i !== increasingNewIndexSequence[j]表示需要移动
    if (j < 0 || i !== increasingNewIndexSequence[j]) {
      move(nextChild, container, anchor );
    } 
    i === increasingNewIndexSequence[j]表示不需要移动
    else {
      j--;
    }
  }
}

• 最长递增子序列:
• 子序列： 子序列中的元素都存在于该序列中，且不要求连续
• 上升：序列中的数字从小到大排序
• 最长：长度最长
• 例如[1,5,7,4,3,2]=>[1,5,7]、[5,4,6,7,8,1]=>[5,6,7,8]。但是在这里getSequence返回是索引数组。例如[1,5,7,4,3,2]=>[0,1,2]、[5,4,6,7,8,1]=>[0,2,3,4]。
• 之前在初始化newIndexToOldIndexMap时,所有的值都赋值为0,然后我们遍历了[s1,e1]找到其中所有节点在c2中的位置并以此为索引重新设置了newIndexToOldIndexMap的值,那么没有被设置的值依旧为0,所以对于newIndexToOldIndexMap[i]===0的节点需要新增。
• 最长递增子序列中的值是不需要发生移动的。

//例子1:
c1:A B C D E
c2:A D B C E
newIndexToOldIndexMap = [4,2,3]
increasingNewIndexSequence = [1,2]
//[4,2,3]分别对应[D,B,C]而最长递增子序列是[2,3]所以
//[2,3]对应的节点[B,C]是不需要移动的。

//例子2:
c1:B D A E C
c2:B E C A D
newIndexToOldIndexMap = [4,5,3,2]
increasingNewIndexSequence = [0,1]
//[4,5,3,2]分别对应[E,C,A,D]而最长递增子序列是[4,5]所以
//[4,5]对应的节点[E,C]是不需要移动的。

• 这是为什么呢？newIndexToOldIndexMap数组的顺序代表的是c2中可能发生移动节点的顺序并且一一对应,同时也是c1需要变换成的顺序,所以他的顺序就是最终结果。而它的值代表的是当前节点在c1中的位置。所以这个值越大代表在c1中的顺序越靠后,由于此时c2中的排列顺序是我们需要的最终结果,所以newIndexToOldIndexMap中的值只要是递增的那么他的顺序就是正确的,也就不需要移动。而需要最长递增子序列是因为需要尽可能多的找到不需要移动的节点,所以总长度减去最长递增子序列就是要移动的节点个数。这也是为什么要找最长递增子序列的原因。
• 当然还有一个问题,为什么一定是由后向前遍历呢？这是因为最终的插入节点的操作使用的是parentNode.insertBefore,也就是说是插入到某个节点之前。由后向前遍历,那么已经遍历过的节点顺序一定是正确的,这样保证了顺序不对的节点插入时需要的anchor是正确的。最后我们再来看看图解。
• 第一次移动:
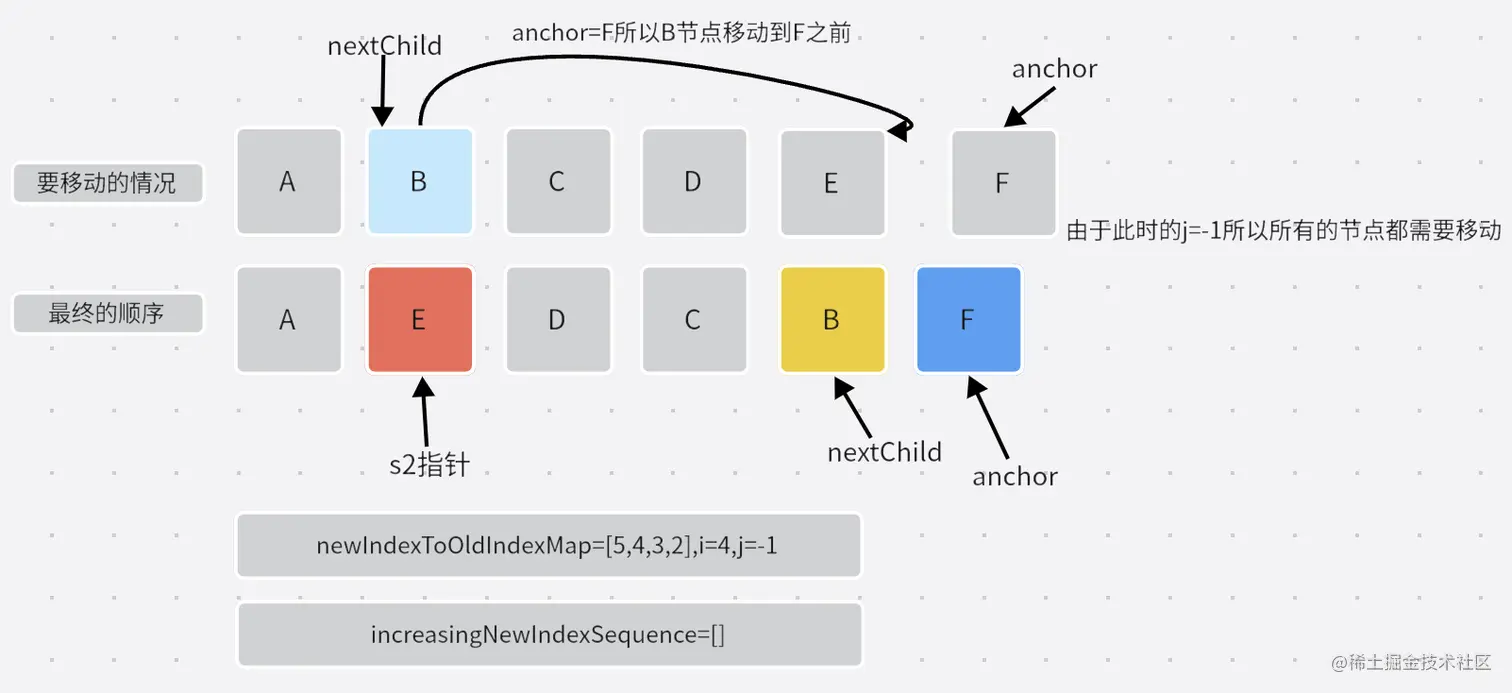
• 第二次移动:
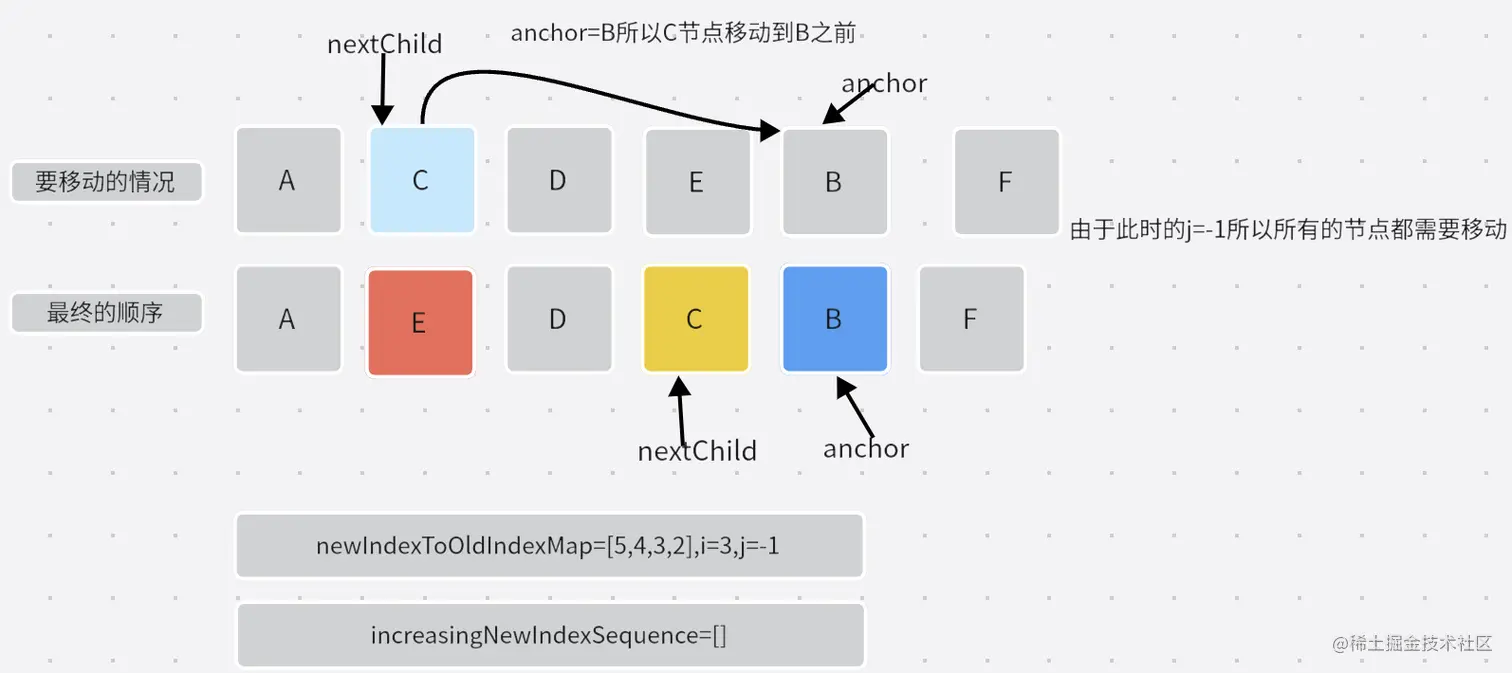
• 第三次移动:
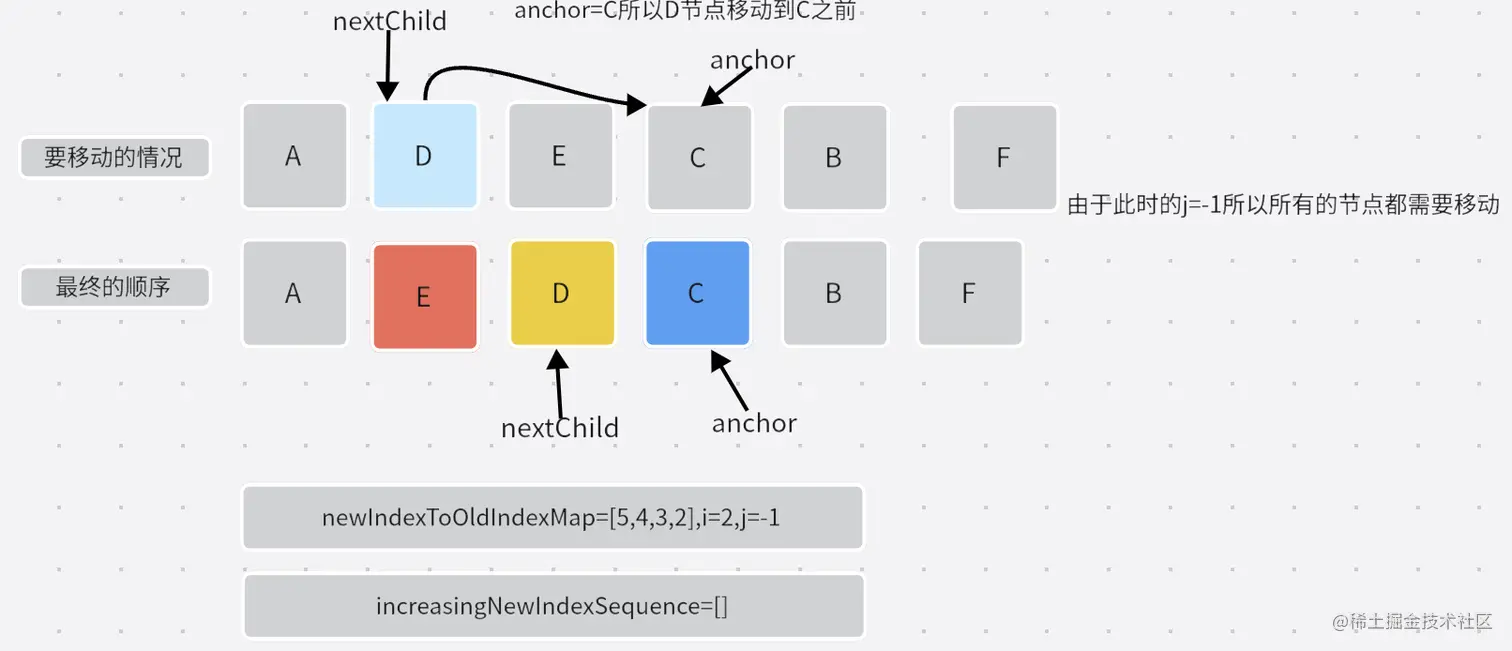
• 第四次移动:
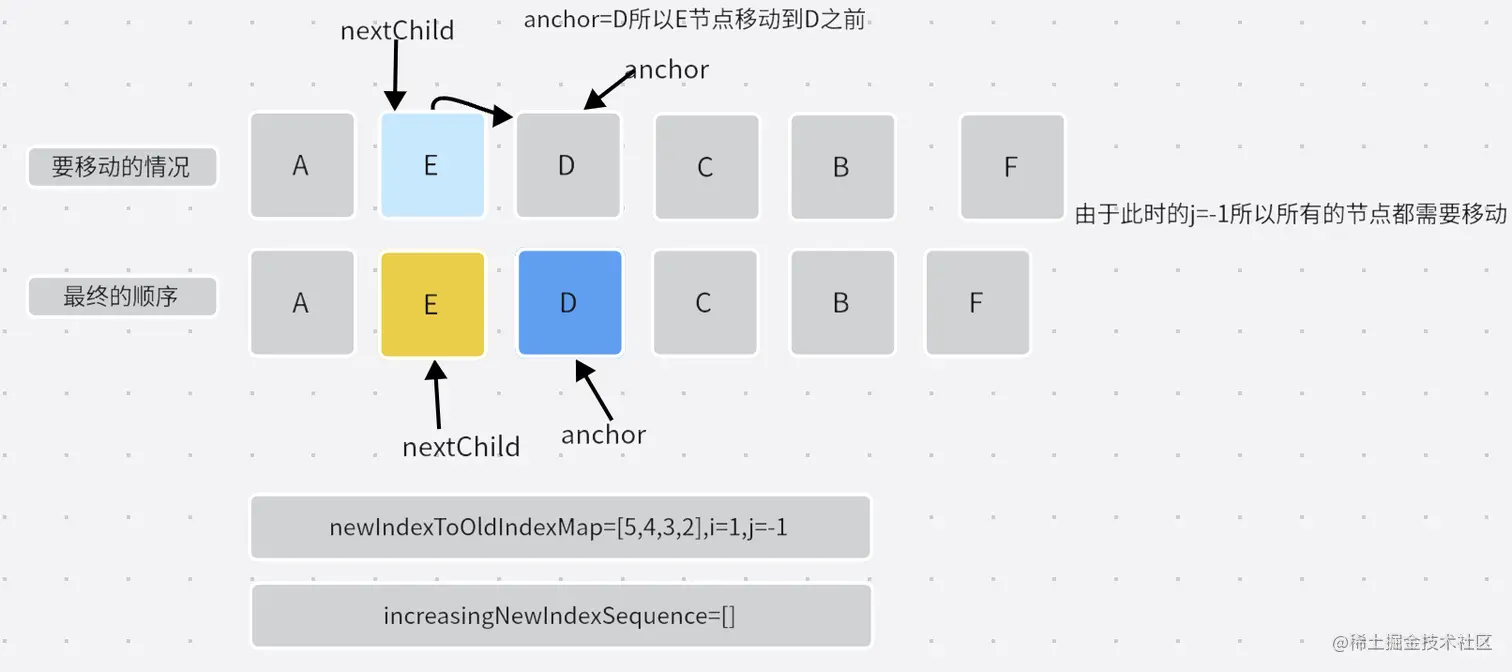
• 这样就完成了整个的移动。

6.步骤总结

• 头指针比较。
• 尾指针比较。
• 新增节点。
• 删除节点。
• 用keyToNewIndexMap保存节点在c2中的具体位置。构建newIndexToOldIndexMap数组,找到最长递增子序列,后序遍历,移动非最长递增子序列中的节点。

patchUnkeyedChildren

//不进行diff比较 根据长度直接挂载或者卸载,
//可见key的重要性,没有key很可能会混乱
const patchUnkeyedChildren = (
  c1, //要比较的beforeVnodeChildren
  c2, //要比较的currentVnodeChildren
  container, //vnode对应的el
  anchor,
) => {
  c1 = c1 || shared.EMPTY_ARR;
  c2 = c2 || shared.EMPTY_ARR;
  const oldLength = c1.length;
  const newLength = c2.length;
  const commonLength = Math.min(oldLength, newLength);
  let i;
  for (i = 0; i < commonLength; i++) {
    const nextChild = (c2[i] = normalizeVNode(c2[i]));
    patch(
      c1[i],
      nextChild,
      container,
      null,
    );
  }
  if (oldLength > newLength) {
    //oldLength:8 newLength:6
    //表示少了两个儿子,卸载newLength之后的children
    unmountChildren(
      c1,
      parentComponent,
      parentSuspense,
      true,
      false,
      commonLength
    );
  } else {
    //oldLength:8 newLength:10
    //挂载新增的两个
    mountChildren(
      c2,
      container,
      anchor,
    );
  }
};

• 这个方法主要用于未使用key的情况,由于没有使用key所以只能通过比较长度来决定卸载和挂载,所以一定要传递key,否则可能出现意想不到的错误。 1.先比较两个数组都有的子节点

c1=[A,B,C]
c2=[A,B]

• 比较A、B子节点。

2. 如果newLength比oldLength大表示需要挂载。

c1=[A,B,C]
c2=[A,B]

• 需要挂载C节点

3. 如果newLength比oldLength小表示要卸载。

c1=[A,B]
c2=[A,B,C]

• 由于没有key,如果通过这种方式进行比较,下面这个例子就会有很大的性能消耗。

c1=[A,B,C,D,E]
c2=[B,A,E,C,D]

• A与B不相同所以会卸载节点再挂载,后面四个节点也一样。如果有key就可以移动节点而不需要卸载再创建。

总结

• 本节我们详细讲解了对于含有key和不含有key的diff方式。相信你一定收获满满吧！