1、二分查找

二分查找的前提是保证序列有序
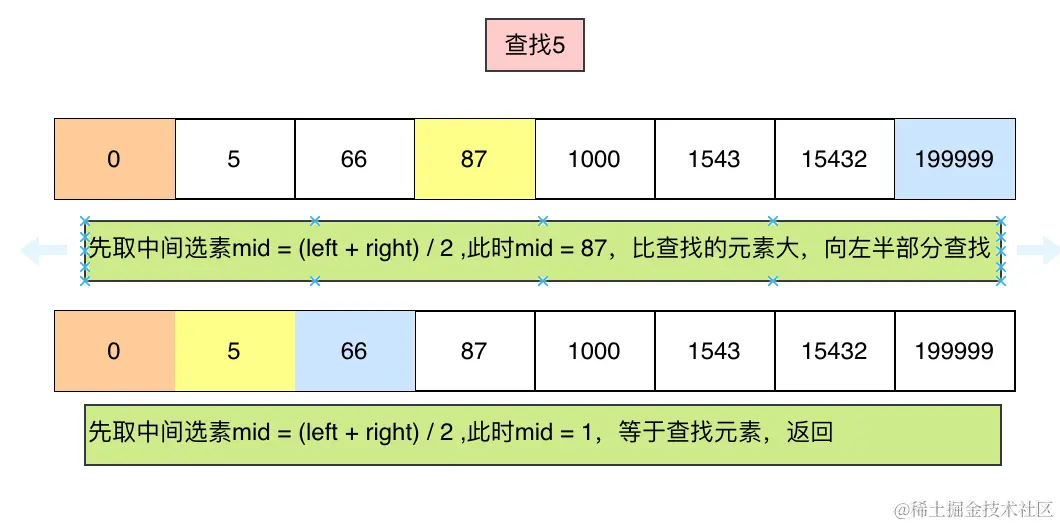
1. 取中间元素进行比较，mid = (left + right) / 2 
2. 和中间值进行比较，如果查找的值大于中间值，则向右半部分进行比较，如果小于则向左半部分进行比较
3. 当mid = 查找的值或者left > right的时候退出

public static <T extends Comparable> int binarySearch(T[] arrays,int left,int right,T target){  
    if (left > right) {  
        return -1;  
    }  
    int mid = (left + right) / 2;  
    if (target.compareTo(arrays[mid]) == -1){  
        return binarySearch(arrays,left,mid - 1,target);  
    } else if (target.compareTo(arrays[mid]) == 1) {  
        return binarySearch(arrays,mid + 1,right,target);  
    }else {  
        return mid;  
    }  
}

2、插值查找

插值查找同二分查找，它mid的取值进行改变，当序列基本有序的时候，插值查找的效率要明显高于二分查找，二分查找每次都找中间值，效率比较低
公式mid = left + (right - left) * (target - arrays[left]) / (arrays[right] - arrays[left]);

public static <T extends Comparable> int insertValueSearch(Integer[] arrays,int left,int right,Integer target){  
    if (left > right || target < arrays[0] || target > arrays[arrays.length - 1]) {  
        return -1;  
    }  
    int mid = left + (right - left) * (target - arrays[left]) / (arrays[right] - arrays[left]);  
    if (target.compareTo(arrays[mid]) == -1){  
        return insertValueSearch(arrays,left,mid - 1,target);  
    } else if (target.compareTo(arrays[mid]) == 1) {  
        return insertValueSearch(arrays,mid + 1,right,target);  
    }else {  
        return mid;  
    }  
}

3、斐波那契查找

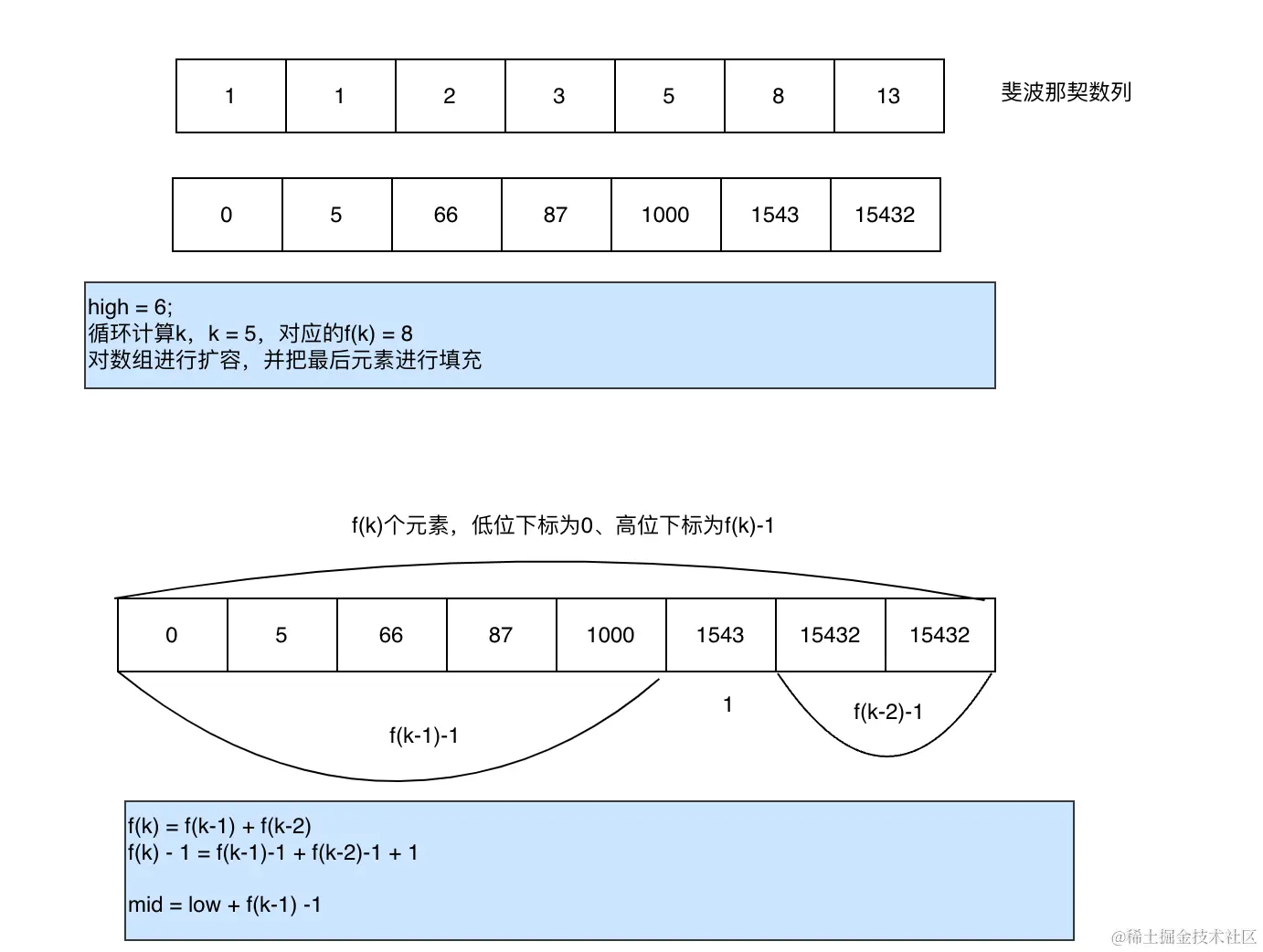
斐波那契数列：f(k) = f(k - 1) + f(k - 2)。
1. 斐波那契查找是根据黄金分割点进行分割查找
2. 及把总长度达到f(k) - 1 ,根据公式分为f(k - 1) -1 和f(k - 2) - 1两个部分
3. 首先要求取k的值，根据循环求取
4. 根据k值计算出总共需要的数组长度，进行扩容，并把最后一个值赋值到扩容的空间
5. 分割查找，跟mid = low + f(k - 1) - 1进行比较
6. 当查找值小于mid时，high = mid - 1,并且令k - 1，因为数列分为两个部分f(k) = f(k-1) + f(k-2)，前半部分为f(k - 1)，后半部分为f(k - 2)。

public static <T extends Comparable> int fibSearch(int[] arrays,int target){  
    int high = arrays.length - 1;  
    int low = 0;  
    int mid = 0;  
    int k = 0;  
    int f[] = fib();  
    while (high > f[k]) {  
        k++;  
    }  
    int[] temp;  
    if (f[k] > arrays.length) {  
        temp = Arrays.copyOf(arrays,f[k]);  
        for (int i = high + 1; i < temp.length; i++) {  
            temp[i] = temp[high];  
        }  
    }else {  
        temp = arrays;  
    }  
  
    while (low <= high) {  
        mid = low + f[k - 1] -1;  
        if (target < temp[mid]) {  
            high = mid - 1;  
            k--;  
        } else if (target > temp[mid]) {  
            low = mid + 1;  
            k -= 2;  
        }else {  
            if (mid <=high) {  
                return mid;  
            }else {  
                return high;  
            }  
        }  
    }  
    return -1;  
}