0 内容提要

本文覆盖概率与计算第二版Chap1-4，9的内容。 这5章内容比较基础，涉及：

• 理论
  • 概率的基本概念
  • 交、并、贝叶斯、全概率计算公式
  • 期望、方差、中位数等数字特征
  • Jensen不等式、Markov不等式、Chebyshev不等式
  • 切诺夫界和Hoeffding界
  • 高斯分布、中心极限定理
• 模型
  • Naive Bayesian Classifier
  • 分支过程
  • 赠券收集问题
  • 秘书问题
• 算法
  • EM算法
  • 均匀分布产生正态分布
  • 多项式判等
  • 矩阵判等
  • 最小割算法
  • 中位数算法

1 理论

这一节的思路是首先建立概率的定义。其实我们探讨随机现象，概率几乎是唯一的原生数值量（连接了物理世界和逻辑世界），其他的期望、方差都是基于概率分布算出来的衍生量。建立概率分布量后，就可以直接按照定义产生一系列概率公式（1.2）。之后我们进一步探索一个概率分布的度量方法，基本方法是一些数字特征（1.3），高级方法是一些尾部不等式（1.4）和更为高级的不等式(1.5)

1.1 基本定义

随机试验：可重复、结果可限定、结果具有随机性

概率的定义，不学习测度理论的话认识深度不会超过本科。两个基本的定义：概率空间和概率，简单摘要不再赘述。

• 概率空间：基本事件集、可行事件集（基本事件子集的集合，对交并补运算封闭）、概率 从可行事件集到实数的映射函数
• 概率：非负、归一（全集概率为1）、和可加 （互斥事件并的概率为各事件概率之和）

频率悖论：假设根据统计数据，30～45岁的人出现癌症的频率是15%，40～70岁的人出现癌症的频率是40%，一个43岁的人，出现癌症的概率如何推断？如果进一步确定了性别、出生地、遗传病史，如何确定统计的样本？越精确，样本越少，越不能说明问题。越不精确，样本虽多，但是统计特性和个体相差越大。

1.2 概率计算公式

和本科学的没啥区别，直接整理一下放在这里了

• 交事件概率
  • 一般事件：$P(AB)=P(A|B)P(B)$
  • 独立事件：$P(AB)=P(A)P(B)$
  • 独立的定义：$P(A|B)=P(A)$
  • n个事件独立：任意事件子集的概率等于概率乘积（很强、超过两两独立）
• 并事件概率（容斥原理）
  • 2个事件：$P(A+B)=P(A)+P(B)-P(AB)$
  • $n$个事件：$P(\sum_{i=1}^nA_i)=\sum_i P(A_i) - \sum_{i<j}P(A_iA_j)+\sum_{i<j<k}P(A_iA_jA_k) - ... + (-1)^{k+1} \sum_{i_1<i_2<...<i_k}P(A_{i_1}...A_{i_k}) +... + (-1)^{n+1} P(A_{i_1}...A_{i_n})$

这里其实有两个小不等式，如果截断只保留前$k$项，$k$是奇数，截断的最后一项是正数，则右侧是个上界。$k$是偶数则右侧是个下界。

• 基础不等式：$P(\cap_i A_i) \le \sum_i P(A_i)$
• 全概率公式：$P(B)=\sum_{i=1}^n P(B|A_i)P(A_i)$，其中$A_i$是一组事件，形成一个覆盖（不重不漏地划分整个概率空间）。
• 贝叶斯公式：$P(A|B)=\frac{P(AB)}{P(B)}=\frac{P(B|A)P(A)}{P(B)}$

正确的看待后验：一个很高的$P(B|A_j)$ 并不意味着有$A_j$就有很大的把握确定$B$。有两个原因：一是因为另一个事件$A_k$可能也有很大的概率导致$B$，二是因为$A_j$可能实在太小了，导致可信度差。如下图：$A_j$是橘色，$B$是绿色，$A_k$是红色

1.3 概率分布的数字特征

期望

• 定义：$E[X]=\sum_x xP(x)$
• 性质：线性性（没有限制条件）
• 定理：$X,Y$独立，$E[XY]=E[X]E[Y], E[X|Y]=E[X]$
• 不等式：$|E[h(x)g(x)]|≤\sqrt{E[h^2(x)g^2(x)]}$
• 引理：对非负离散随机变量$X$, $E[X]=\sum_{i=1}^\infty Pr[X\ge i]$

简单证一下：$\sum_{i=1}^\infty Pr[X\ge i]=\sum_{i=1}^\infty \sum_{j=i}^\infty Pr[X=j]=\sum_{j=1}^\infty \sum_{i=1}^j Pr[X=j]=\sum_{j=1}^\infty j Pr[X=j]=E[X]$
这里第二个等号的重排原理见下图，因为都是正数，这样重排合理。第三个等号是因为对i求和就是完全一样的j个数加起来。

条件期望

• 定义：$E(X|Y)=\sum_x xP(x|Y)$。这个东西本质是一个关于$Y$的函数，而$Y$是一个随机变量，所以条件期望也是随机变量。
• 性质：$E[E[X|Y]]=E[X], E[Z|X]=E[E[Z|Y,X]|X]$

方差

• 定义：$Var[X]=E[(X-E[X])^2]$
• 性质：$Var[X]=E[X^2]-(E[X])^2$

矩

• 原点矩：$E[X^r]$
• 中心矩：$E[(X-E[X])^r]$

协方差

• 定义：$Cov[X, Y]=E[(X-E[X])(Y-E[X])]$
• 性质；$Var[X+Y]=Var[X] + Var[Y] + 2Cov[X,Y]$
• 推论：$X,Y$独立,$Cov[X,Y]=0$

协方差和相关系数
令$m_{ij}=E[X^i Y^j], c_{ij}=E[(X-EX)^i(Y-EY)^j]$
相关系数:$\rho=\frac{c_{11}}{\sqrt{c_{20}c_{02}}}$
为何$|\rho|\le 1$?
构造法：$Q(\lambda)=E[(\lambda(X-EX)(Y-EY))^2]=\lambda^2 c_{20}+2\lambda c_{11}+c_{02}$
非负数的期望肯定非负，所以$Q(\lambda) \ge 0$
由$\Delta \le 0\rightarrow |\rho|\le 1$

中位数

• 定义：一般中位数是从统计那里学来的，对于随机变量，其中位数是满足$Pr[X<m]=Pr[X>m]$的$m$
• 性质：中位数是使得$E[|X-m|]$的值最小的$m$。

关系

• 期望与方差的关系： $E[X]$是使$E[(X-c)^2]$最小的$c$，展开求导即可证明。并且最小值恰好是方差。
• 中位数、期望和方差的关系：如果$X$有$\sigma=\sqrt{Var(X)}< \infty$，那么$|\mu - m| \le \sigma$

证明：$|\mu - m| = |E[X]-m| = |E[X-m]|\le E[|X-m|]\le E[|X-\mu|]\le \sqrt{E[(X-\mu)^2]}=\sigma$ 第3个不等号是Jensen不等式，第4个是中位数的性质，第5个是Jensen不等式

两个随机变量的关系

• 不相关：$Cov[X,Y]=0$
• 独立：$E[XY]=E[X]E[Y]$
• 正交：$E[XY]=0$

1.4 高级度量方法

高级度量方法主要有3个不等式：Jensen、Markov、Chebyshev

Jensen不等式

这个其实严格来说不算是概率的不等式，只是函数凸性的利用。 下凸函数$f$，有$E[f(X)]\ge f(E[X])$

严格的证明是在$\mu$处taylor展开，不严格的证法是画图，但不严格的其实只能证明有限项的求和正确定。

Markov不等式

非常经典，对于非负变量$X$，$Pr[X\ge a]\le\frac{E[X]}{a}$。

证明，构造指示器变量$I$，在$X>a$时取1，否则取0，则有$I\le \frac{X}{a}$，然后对I求期望即可。

Chebyshev不等式

对任意$X$, $Pr[|X-E[X]|\ge a]\le \frac{Var[X]}{a^2}$

证明 $Pr[|X-E[X]| \ge a] = Pr[(X-E[X])^2 \ge a^2]$，对后者的平方作为随机变量使用Markov不等式即可。

• 技巧：一般这个a会取一个和方差或期望相关的数值，这样不等式右侧会更优雅。

1.5 更高级的界

矩函数

• 定义：对随机变量$X$，定义矩函数$M_X(t)=E[e^{tX}]$
• 性质1：$E[X^n] = M^{(n)}_X(0)$
• 性质2：矩函数唯一定义分布
• 性质3：两个独立随机变量 $M_{X+Y}(t)=M_X(t)M_Y(t)$

切诺夫界

$Pr[X \ge a] = Pr[e^{tX} \ge e^{ta}] \le \min_{t \ge 0}\frac{E[e^{tX}]}{e^{ta}}$

最后一步用的是Markov界。注意这个里面虽然取min可以让bound更紧，但是t有时候也为了形式简洁不那么紧。

通常包含的两个技巧：

• 高频的使用$e^x \ge x + 1$这个不等式。
• 右侧化简到只剩一个e，taylor展开。

霍夫丁界

对一系列相互独立的随机变量$X_1, .., X_n$，若$E[X_i] = \mu$, $Pr[a \le X_i \le b] = 1$，则有$Pr[|\frac{1}{n}\sum_i X_i - \mu|\ge \epsilon]\le 2e^{-2n\epsilon^2 / (b - a)^2}$

用不太严格的话来说，度量了一系列独立的同界同均值变量的均值误差界

lemma 对于$E[X]=0$的有界[a, b]随机变量，对一切$\lambda > 0$, 有$E[e^{\lambda X}]\le e^{\lambda^2(b - a)^2/8}$.

证明思路利用指数函数的下凸性质
1 构造$e^{\lambda x} < \frac{b - x}{b - a}e^{\lambda a}+\frac{x - a}{b - a}e^{\lambda b}$
2 所以 $E[e^{\lambda x}] \le \frac{b}{b - a}e^{\lambda a}- \frac{a}{b - a}e^{\lambda b}$
3 重写上面这个式子右侧，令$\phi(t)=-\theta t+\ln(1-\theta+\theta e^t)$,其中$\theta=\frac{-a}{b - a} > 0$，那么右侧就变成了$e^{\phi(\lambda(b-a))}$
4 对$\phi$函数taylor展开可以发现他小于$\frac{1}{8t^2}$，带入可证。

利用lemma，可以证明霍夫丁界

1 构造$Z_i = X_i - E[X_i], Z = \frac{1}{n}\sum_i Z_i$
2 $Pr[Z\ge \epsilon]=Pr[e^{\lambda Z} \ge e^{\lambda \epsilon}]\le e^{-\lambda \epsilon}\prod E[e^{\lambda Z_i/n}] \le e^{-\lambda \epsilon + \lambda^2(b-a)^2/8n}$
3 取$\lambda=\frac{4n\epsilon}{(b-a)^2}$，可证一半，对于小于的部分也差不多。

更一般的。如果这n个随机变量的界彼此不一样，那么

$Pr[|\frac{1}{n}\sum X_i - \mu|\ge \epsilon] \le 2e^{-2\epsilon^2/\sum(b_i-a_i)^2}$

1.6 正态分布

标准正态

$N(0,1)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$

• 性质1：线性变换也是正态，如果$Z\sim N(0,1)$，而$X=\sigma Z + \mu$，那么$X\sim N(\mu,\sigma^2)$，$N(\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$
• 性质2:独立正态的和也是正态，且$N(\mu_1, \sigma^2_1)+N(\mu_2, \sigma^2_2)=N(\mu_1+\mu_2, \sigma^2_1 + \sigma^2_2)$
• 母函数：$M_X(t)=e^{\mu t + \frac{t^2\sigma^2}{2}}$

高维正态

$Y=(Y_1, ..., Y_n)=\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}e^{-\frac{1}{2}(Y-\mu)^T\Sigma^{-1}(Y-\mu)}$

其中，$\mu$是均值向量，$\Sigma$是协方差矩阵。上述密度存在的前提是$\Sigma$满秩，不然逆不存在。

中心极限定理

• n个独立同分布的随机变量，均值和方差分别为$\mu, \sigma^2$，那么$\lim_{n\rightarrow\infty}\Pr(a\le \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\le b)$依分布收敛于$\Phi(b)-\Phi(a)$
• n个独立变量，期望方差分别是$\mu_i, \sigma^2_i$，如果随机变量绝对值有界且$\lim_{n\rightarrow\infty}\sum_i^n\sigma^2_i=\infty$，则$\Pr[a \le \frac{\sum(X_i-\mu_i)}{\sqrt{\sum\sigma_i^2}}\le b]$依分布收敛于$\Phi(b)-\Phi(a)$
• 配合Chebyshev不等式可以导出弱大数定律:
  $X_i$是iid且均值方差分别为$\mu, \sigma$, $\mu_n=1/n\sum_{i=1}^n X_i, P(|\mu_n-\mu|≥\delta)≤\frac{\sigma^2}{n\delta^2}$

2 模型

这一节介绍基本理论较为通用的应用，他们一般不针对具体问题，或者所研究的问题具有通用性。

Naive Bayesian Classifier

这个其实很简单，把名字里的三个单词倒过来看就行了。

• 首先是Classifier，说明解决的是分类预测问题，即对于给定一个样本（具有$k$个属性）$(o_1, o_2, ..., o_k)$，返回最有可能的分类。
• 第二个词是Bayesian，说明这个预测问题是基于贝叶斯的方法来的，那就是要求后验概率，即$Pr[C=c_j|o_1, o_2, ..., o_k]$的概率。 利用贝叶斯公式，这个概率可以转化成$\frac{P(o_1, o_2, ..., o_k|c_j)P(c_j)}{P(o_1, o_2, ..., o_n)}$。其中分母比较难求，不过一般就是用来归一化的系数所以不需要求，更重要的是分子如何求。
• 这时就用到最后一个单词Naive了，naive的意思是假设样本所有的属性是彼此独立的，那么似然度就可以写成$P(o_1, o_2,..., o_k|c_j)=\prod_{i=1}^kP(o_i|c_j)$. 现在，如果有了训练数据，只要求出似然度中的$k\times c$个概率$P(o_i|c_j)$和$c$个先验概率$P(c_j)$即可。这些概率很容易算，直接根据样本数据中满足条件的数据数量的频率推算即可。比如$P(c_j)$就是训练数据中类别为$c_j$的占比。而$P(o_i|c_j)$就是样本中第i个属性取值为$o_i$且类别为$c_j$的样本占类别为$c_j$样本的比例。

分支过程

这个对应原书2.3节，这一块他举的例子是程序的调用过程，其实用文字说不太直观，这里画一个图来表示这个过程。 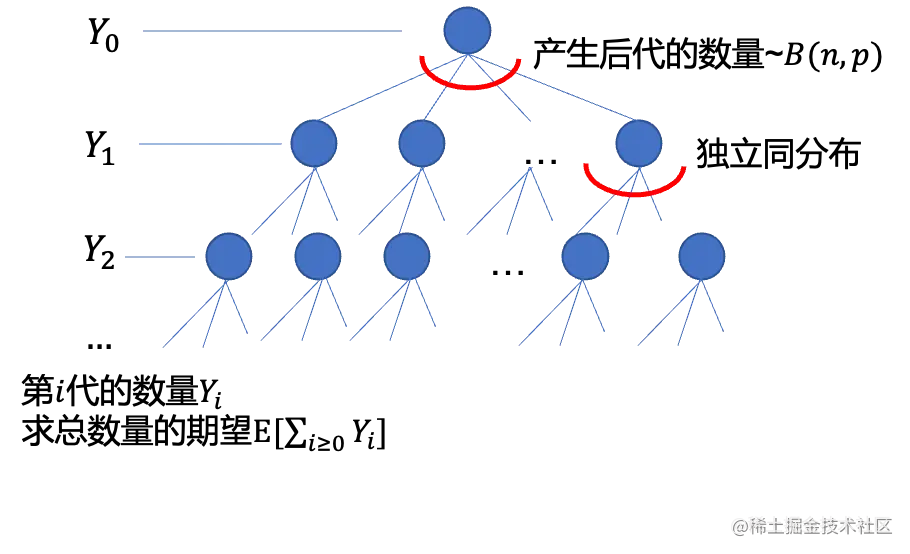这里用到的思想是逐代递推，假设我们已经知道$Y_{i-1}=y_{i-1}$，尝试求$Y_i$的期望:$E[Y_i|Y_{i-1}]=npy_{i-1}$。

这个其实很直观，因为上一层有$y_{i-1}$个结点，每一个分叉的期望数量是$np$且相互独立，那这一层总的期望数量就是$npy_{i-1}$

因此$E[Y_i]=E[Y_i|Y_{i-1}]=npE[Y_{i-1}]$，一直递推到$Y_0$，而$Y_0=1$为定值，所以$E[Y_i]=(np)^i$。其实对0也成立。

所以总数$E[\sum_{i\ge0}Y_i]=\frac{1 - (np)^i}{1-np}$

赠券收集问题

• 问题描述：现在有$n$种券，需要通过开盒子收集。每个盒子等可能地包含一张券。问平均需要开多少盒子才能集全所有券（即每一种至少一张）？

这里用到的思想和分支很像，可以称之为状态递推。

我们关心的是赠券收集的情况，而这个过程又是分步骤的，所以可以把最终目标拆分成一系列状态步骤。本问题中，定义状态$S_k$为恰好收集了$k$种券（即有n-k种券的数量为0）。状态转移图如下

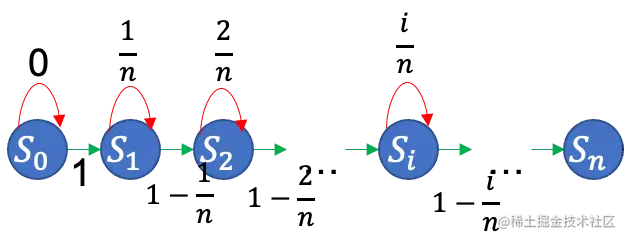
红色箭头表示在当前状态开了一个盒子，结果奖券种类没有增加，停留在当前状态。绿色表示种类增加了，进入下一状态。这个概率取决于当前手上有的种类数。有的种类越多，那开盒能得到新种类券的概率就越低。现在需要求从$S_0$转移到$S_n$平均需要多少次转移。

定义$X_k$表示在$S_k$状态开盒的数量，那么保持在$S_k$的概率是$\frac{k}{n}$，进入到下一状态的概率是$1-\frac{k}{n}$。所以很容易列出

$E[X_k]=\sum_{i=0}^\infty iPr[X_k=i]=\sum_{i=0}^{\infty} i(\frac{k}{n})^{i-1}(1-\frac{k}{n})=\frac{n}{n - k}$。这里最后一步用到了级数求和公式。

而最终要求的其实是$X_0$到$X_{n-1}$（因为最后一个状态不需要开盒子）。

所以$E[\sum_{k=0}^{n-1}X_k]=\sum_{k=0}^{n-1}\frac{n}{n - k}=n\sum_{k=0}^{n-1}\frac{1}{n-k}=n\sum_{i=1}^n\frac{1}{i}=\Theta(n\log n)$。

这个结论很有意思，作为一种营销策略其实很失败。因为如果我们希望通过增加券的种类来激励消费者购买更多产品，增加奖券的方法能带来的销量增长只比线性好了一点点。所以肯定不会等可能的投放奖券。

首中问题的随机变量服从几何分布，如果命中概率为p，那么期望和方差分别为$\frac{1}{p}$和$\frac{1-p}{p^2}$。直接按照定义求解需要求复杂的级数求和。比较tricky的方法是利用分布的无记忆性递推。$E[X]=p+(1-p)(1+E[X])$

秘书问题（习题2.32）

例题：招聘问题。有一串n个数字均匀分布，你每次看一个，看完决定要还是不要，不要之后就再也不能反悔，如何要到最大数字？

策略：先看前k个，从第k+1个开始，遇到比k大的就停止，关键是这个k如何选择。

为了让概率最大，关于k求导，得到k=N/e。

集合的均衡

给定义个$n \times m$的矩阵A，每个位置的值为0或1，求一个$m$维向量$b$，$b$的每一个元素只能取1或-1，使得$\min \max_i c_i$，其中$c = Ab$

一个很简单的方法是：$b$的每一个位置，等概率随机选择1或-1。这个方式看似完全忽略了$A$的内容，但他竟然是最优的，即，$\min \max_i c_i=O(\sqrt{4m\ln n})$，超越这个上限的概率n的增大而趋于0。

$Pr[||Ab||_{\infty} \ge \sqrt{4m\ln n}] \le 2e^{-4n\ln n/2k} \le \frac{2}{n^2}$

这里其实分类讨论，对矩阵的某一行，如果1的数量（设为k）小于$4m\ln n$，那显然成立。如果超过$k$，那么这$k$个对应的向量的位置是+1和-1的二项分布，利用切诺夫界可以求出上界。

3 算法

EM算法

EM的主要应用于样本来源于多个未知分布，但是不知道每个样本属于哪个分布的情况。此时需要估计的参数既有分布本身的，也有属于哪个分布的概率。然后我们就利用迭代的思想。一开始随便取，然后计算似然函数，然后对属于何分布的参数求偏导计算，之后更新之（E-step）。更新了该参数，再利用MLE计算其他分布里参数的估计（M-step）。

特点是每次迭代似然度都在提升，至少收敛到局部最优。

用均匀分布产生正态分布

这是一个很实用的问题。核心是对CDF的理解：0-1上的概率转移到了其他CDF上那么分为点是多少

1 最简单的近似

利用中心极限定理，一系列0-1上的均匀分布的求和然后标准化即可。一个良好的近似取12个就足够了即$X=(\sum_{i}^{12}U_i)-6$。

它具有均值0，方差1，但区间是在$[-6,6]$。

2 极坐标转化

考虑两个独立的标准正态的联合分布:$F(x',y')=\int_{-\infty}^{y'}\int_{-\infty}^{x'}\frac{1}{2\pi}e^{-(x^2+y^2)/2}dxdy$

通过极坐标变换，可以分解成$F(r',\theta')=\frac{\theta'}{2\pi}(1-e^{-(r')^2/2})$

可以看到，$r$和$\theta$是分属两项的，说明极坐标变换完之后还是独立的。而前面整体恰好是一个$[0,2\pi]$均匀分布的CDF，而后面那一项如果硬看作(0,1)上的均匀分布的话，另它$=1-V$。这样经过一系列代换，同时注意到$1-V$和$V$都是0-1上的均匀分布可以直接替换，可以得到两个独立的标准正态$X=\sqrt{-2\ln V} \cos(2\pi U), Y=\sqrt{-2\ln V} \sin(2\pi U)$

3 拒绝采样避免三角函数计算

为了避免三角函数，还可以进一步改进，把$U$和$V$线性映射到(-1,1)区间，然后$S=U^2+V^2$。如果$S>1$，说明在单位圆外部重新采样。在内部可以利用$U/\sqrt{S}$来表示cos, $V/\sqrt{S}$来表示sin。然后$S$也是0-1上的均匀分布，所以$\ln S$可以替换$\ln V$

$X=U\sqrt{\frac{-2\ln S}{S}}, Y=V\sqrt{\frac{-2\ln S}{S}}$，$S$是$U$和$V$的平方和。

算法部分研究的问题更具体，因此我更侧重于这些算法背后利用的思想，而具体技术细节和理论推导不在赘述。

• 随机探针思想 多项式判等和矩阵判等两个问题透露出一种共同的思想。对于多项式，探针是函数的自变量，而对于矩阵，探针是一个0-1向量。因为探针是随机抽取的，所以需要分析其失效的情况以及采样到失效情况的概率。

• 局部处理思想 中位数算法中，相较于对整体排序，该算法选取局部$\Theta(\sqrt{n})$规模的元素进行排序。从而控制排序的元素规模来保证时间复杂度。局部处理的代价是可能miss包含中位数的范围。体现了trade-off的特点。

• 事后分析思想 最小割算法中，缩边本质是赌收缩的两个点在割的一侧，至于赌的对不对，其实是靠事后分析，即在已知最小割规模的情况下分析持续选对边的概率。

分析技巧

• 延迟决策原理：多个随机变量时，把一部分看作随机，其他看作固定。
• 单边错误重复

习题 Notes

Chap1

1.9

• 题目：抛一枚均匀硬币n次，对于k>0，计算连续出现$log_2(n)+k$次正面向上的概率上界。
• Answer： 设事件$E_i$表示从第i次开始出现连续$log_2(n)+k$次正面向上，则$P(E_i) = (\frac{1}{2})^{log_2(n)+k}=\frac{1}{n2^k}$

所以$P(E_1+E_2+...+E_{n-(log_2(n)+k + 1)})\le \sum P(E_i) = \frac{n - log_2(n)+k+1}{n2^k}\le \frac{1}{2^k}$

1.15

• 题目：抛10个六面体骰子，点数之和能被6整除的概率
• Answer：$p_i^j$表示i个骰子点数和mod 6余j的概率。那么$p_{10}^0=\frac{1}{6}p_9^0 + \frac{1}{6}p_9^1 + \frac{1}{6}p_9^2 + \frac{1}{6}p_9^3 + \frac{1}{6}p_9^4 + \frac{1}{6}p_9^5 = \frac{1}{6}(\sum_j p_9^j)=\frac{1}{6}$.

1.18

• 题目：一个离散函数定义域是0～n-1的整数，值域是0～m-1的整数，有1/5的值被篡改了，但是函数有一个性质$F((x+y)\% n) = (F(x)+F(y))\% m$，问你如何设计一个算法，对任意的$z$，至少以$\frac{1}{2}$的概率给出正确结果。
• Answer：这个乍一看不好理解，如果我直接输出$F(z)$，似乎错误的概率只有$\frac{1}{5}$，为啥这样不行呢？这里其实使用了对手模型，即，我们假设给你输入z的人就是篡改你函数表的人，那如果你设计这种算法，他可以直接输入他篡改的那些项，你的错误概率就是100%了。

为了应对这种攻击性的输入，算法必须具有内生的随机性来避免这个问题。这个可以联想随机快速排序，他通过内生的随机性，使得不论如何构造测试用例，期望复杂度始终是$O(n\log n)$的。

因此，这里考虑利用这个函数的性质，把输入转移到其他的函数值上。随机sample一个x，然后令y=(z-x) % n。这样把$(F(x)+F(y)) \%m$作为结果输出。这样，不论你输入的z是不是被篡改的，我总是会转化成另外两个输入的结果。而这个结果错误的概率为$Pr[x被篡改+y被篡改]\le Pr[x] + Pr[y] = \frac{2}{5}$。

正确概率超过1/.

1.23

• 题目：利用最小割随机化算法分析，至多有$n(n-1)/2$个不同的最小割。
• Answer：书中证明了一个最小割被返回的概率是$\frac{2}{n(n-1)}$，那么k个的概率求和小于1，就可以了。

Chap 2

2.7/2.24 无记忆性

• 2.7: X和Y是独立的几何随机变量，概率分别为p和q。求X=Y的概率。

• answer 这里利用了无记忆性 $Pr[X=Y] = Pr[X_1 = Y_1= 1]Pr[X'=Y'] + Pr[X_1=Y_1=0]Pr[X'=Y'] = pqPr[X=Y] + (1-p)(1-q) Pr[X=Y]$，得到关于Pr的方程，求解即可。后面几个差不多。

• 2.24 掷骰子连续两个6的期望次数

• answer 设X是第一次出现6的次数，Y是连续两个6的次数。那么在X出现之后，有1/6的概率Y=X+1，而其余5/6的概率Y=X+Y'，Y'表示6的状态被清零了，需要重新投掷，那么在此出现两个6的概率按照无记忆性其实分布和Y是一样的。

因此$E[Y]=\frac{1}{6}E[X+1] + \frac{5}{6}E[X + Y]$，显然$E[X]=6$，则$E[Y]=42$

2.20/2.21 指示器变量思想

• 2.20: n个数字随机排列，求不动点的期望数量

• answer $X_i$表示第i个位置是不动点$Pr[X_i=1]=\frac{1}{n}$. $E[\sum X_i]=1$

• 2.21: 随机排列排序过程元素移动距离

• answer $X_{ij}$表示把元素i从j移动到i的距离，取值为$|j-i|$或0，概率分别为$1 - 1/n$和1/n。求和即可。

2.2

• question 从26个小写字母随机采样100000次，出现proof的期望次数是多少。
• answer 各路答案的思路，是(1000000 - len(proof)) * (1 / 26)^len(proof)，这个数值约等于0.085，我实际用python算了一下大概也确实是。这个答案基本是正确的。不过我没想清楚是怎么回事。感觉是一个近似解

Remakrs

• 概率、期望的求解：利用无记忆性列出方程
• 多步骤问题使用状态转移图
• 指示器变量思维