线性回归

一、概述

假设有以下数据：

\begin{gathered} D=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} \\ x_i \in \mathbb{R}^p, y_i \in \mathbb{R}, i=1,2, \cdots, N \\ X=\left(x_1, x_1, \cdots, x_N\right)^T=\left(\begin{array}{c} x_1^T \\ x_2^T \\ \vdots \\ x_N^T \end{array}\right)=\left(\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 p} \\ x_{21} & x_{22} & \cdots & x_{2 p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{N 1} & x_{N 2} & \cdots & x_{N p} \end{array}\right)_{N \times p} \\ Y=\left(\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_N \end{array}\right)_{N \times 1} \end{gathered}

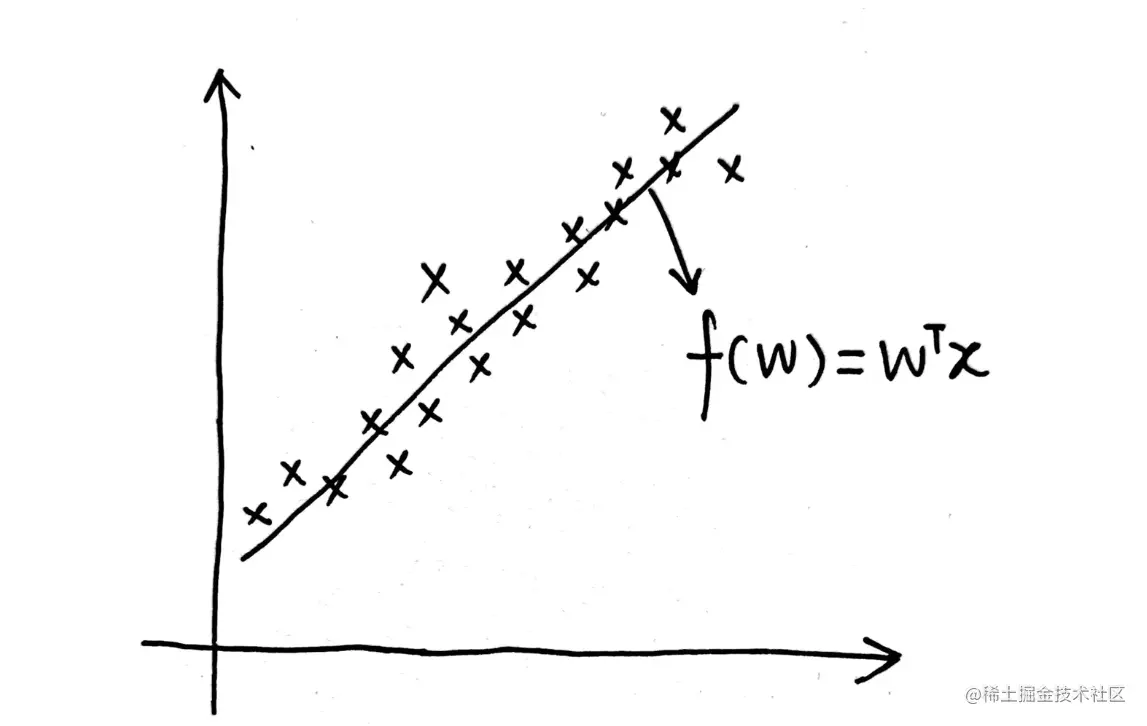
这些数据符合下图关系 (以一维数据为例)，这里的函数 $f(w)$ 忽略了偏置 $b$ :

二、最小二乘估计

L(w)=\sum_{i=1}^{N}\left \| w^{T}x_{i}-y_{i}\right \|_{2}^{2}\\ =\sum_{i=1}^{N}(w^{T}x_{i}-y_{i})^{2} \\ =\underset{\underset{\underset{w^{T}X^{T}-Y^{T}}{\underbrace{w^{T}\begin{pmatrix} x_{1} & x_{2} & \cdots & x_{N} \end{pmatrix}-\begin{pmatrix} y_{1} & y_{2} & \cdots & y_{N} \end{pmatrix}}}}{\underbrace{\begin{pmatrix} w^{T}x_{1} & w^{T}x_{2} & \cdots & w^{T}x_{N} \end{pmatrix}-\begin{pmatrix} y_{1} & y_{2} & \cdots & y_{N} \end{pmatrix}}}}{\underbrace{\begin{pmatrix} w^{T}x_{1}-y_{1} & w^{T}x_{2}-y_{2} & \cdots & w^{T}x_{N}-y_{N} \end{pmatrix}}}\begin{pmatrix} w^{T}x_{1}-y_{1}\\ w^{T}x_{2}-y_{2}\\ \vdots \\ w^{T}x_{N}-y_{N} \end{pmatrix}\\ =(w^{T}X^{T}-Y^{T})(Xw-Y)\\ =w^{T}X^{T}Xw-w^{T}X^{T}Y-Y^{T}Xw+Y^{T}Y\\ =w^{T}X^{T}Xw-2w^{T}X^{T}Y+Y^{T}Y

接下来通过对 $w$ 求导就可以解得参数 $w$ :

\begin{gathered} \hat{w}=\operatorname{argminL}(w) \\ \frac{\partial L(w)}{\partial w}=2 X^T X w-2 X^T Y=0 \\ \text { 得出 } w=\underbrace{\left(X^T X\right)^{-1} X^T}_{X^{+}, \text {伪逆 }}Y \end{gathered}

以上未考虑偏执 $b$ ，如果考虑的话则可以为 $w$ 添加一个维度，同时也为 $x$ 添加一个维度并使得添加的维度的值为 1 ，然后使用同样的求解方法即可。

其中有几个注意点：

从 $w^{T}x_{1}-y_{1}...$ 到 $Xw-Y$ ，是矩阵的转置造成的
$w^{T}X^{T}Y$ 与 $Y^{T}Xw$ 能合并是因为他们均为一维。
科普几个矩阵转置求导的知识
1. 矩阵转置

\begin{aligned} & (\mathrm{A}+\mathrm{B})^{\mathrm{T}}=\mathrm{A}^{\mathrm{T}}+\mathrm{B}^{\mathrm{T}} \\ & (\mathrm{AB})^{\mathrm{T}}=\mathrm{B}^{\mathrm{T}} \mathrm{A}^{\mathrm{T}} \end{aligned}

2.矩阵求导

\begin{aligned} & \frac{\partial \mathrm{Ax}}{\partial \mathrm{x}}=\mathrm{A}^{\mathrm{T}} \\ & \frac{\partial \mathrm{Ax}}{\partial \mathrm{x}^{\mathrm{T}}}=\mathrm{A} \\ & \frac{\partial \mathrm{x}^{\mathrm{T}} \mathrm{A}}{\partial \mathrm{x}}=\mathrm{A} \\ & \frac{\partial \mathrm{x}^{\mathrm{T}} \mathrm{Ax}}{\partial \mathrm{x}}=\left(\mathrm{A}^{\mathrm{T}}+\mathrm{A}\right) \mathrm{x} \end{aligned}

三、线性回归的几何解释

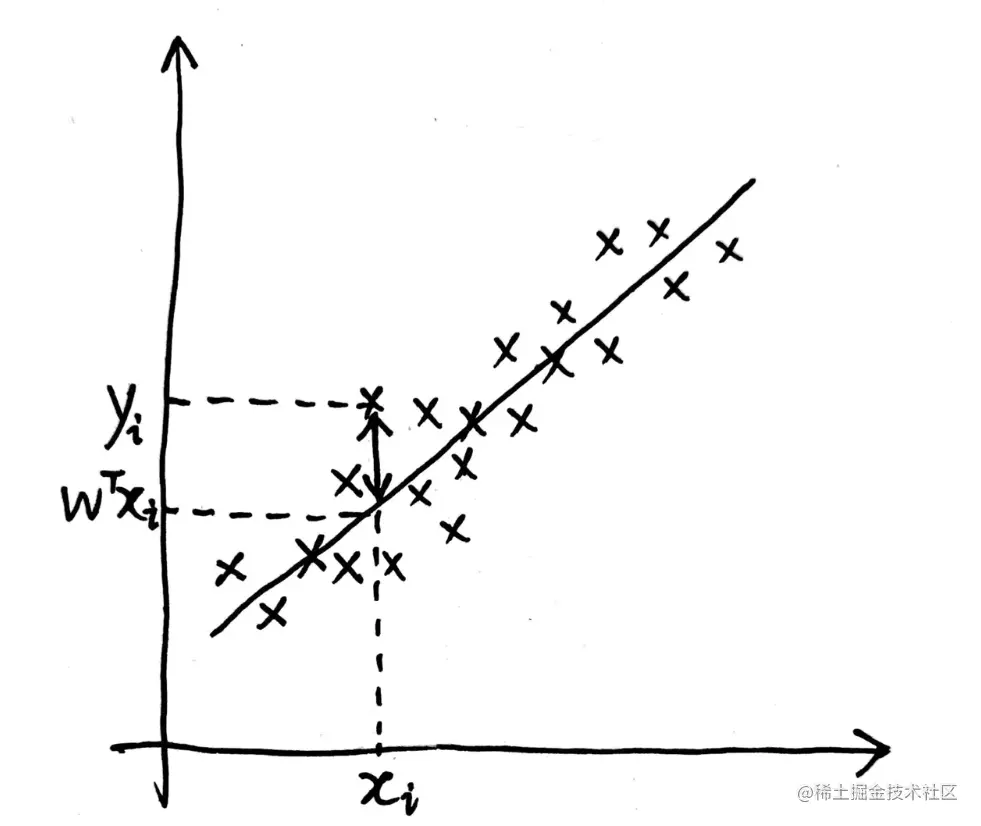
每个样本点的误差的总和使用最小二乘法可以看做损失函数是每个样本的误差的总和，每个样本的误差即是 $y_i$ 与 $w^T x_i$ 的差，如下图所示:

$Y$ 在 $X$ 的列空间上的投影

一组向量的生成子空间 (span) 是原始向量线性组合后所能抵达的点的集合。确定方程 $A x=b$ 是否有解，相当于确定向量 $b$ 是否在 $A$ 列向量的生成子空间中。这个特殊的生成子空间被称为 $A$ 的列空间 (column space) 或者 $A$ 的值域 (range)。

我们的目的是为了求解 $w$ 使得 $X w=Y$ ，显然这个方程一般是无解的，即 $Y$ 一般不在 $X$ 的列空间中，因为样本点一般是散落在某条直线周围，所有的样本点准确地落在同一条直线上的情况少之又少。

对于 $X w=f(w)$ ，为了使 $f(w)$ 与 $Y$ 最接近，则 $f(w)$ 就应该是 $Y$ 在 $X$ 的列空间中的投影，如下图所示，以 $p=2$ 为例:

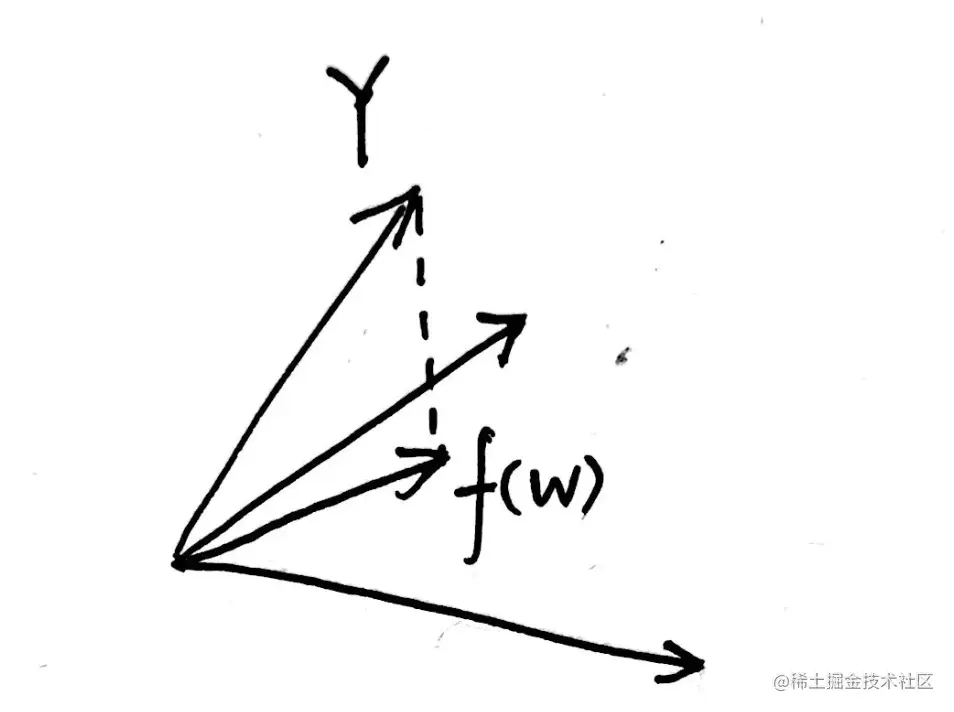
$Y-X w$ 就应该与每一个 $\left(\begin{array}{c}x_{1 i} \\ x_{2 i} \\ \vdots \\ x_{N i}\end{array}\right)$ 都垂直，即 $X^T(Y-X w)=0_{p \times 1}$ ，则可以直接解得 $w=\left(X^T X\right)^{-1} X^T Y$

四、最小二乘法与极大似然估计

可以认为实际值与估计值之间的差是一个高斯噪声，即 $y$ 和 $f(w)$ 满足关系 $y=f(w)+\varepsilon=+\varepsilon$ ，其中 $\varepsilon$ 是高斯噪声，满足 $\varepsilon \sim N\left(0, \sigma^2\right)$ ， $w^T x$ 可以看做常数，因此 $y \mid x ; w \sim N\left(w^T x, \sigma^2\right)$ ，即 $P(y \mid x ; w)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{\left(y-w^T x\right)^2}{2 \sigma^2}\right\}$

可以使用极大似然估计法来进行求解:

\begin{gathered} & L(w)=\log P(Y \mid X ; w) \\ & =\log \prod_{i=1}^N P\left(y_i \mid x_i ; w\right) \\ & =\sum_{i=1}^N \log P\left(y_i \mid x_i ; w\right) \\ & =\sum_{i=1}^N\left(\log \frac{1}{\sqrt{2 \pi}}+\log \exp \left\{-\frac{\left(y_i-w^T x_i\right)^2}{2 \sigma^2}\right\}\right) \\ & =\sum_{i=1}^N\left(\log \frac{1}{\sqrt{2 \pi}}-\frac{\left(y_i-w^T x_i\right)^2}{2 \sigma^2}\right) \\ & \hat{w}=\operatorname{argmax} L(w) \\ & =\underset{w}{\operatorname{argmax}} \sum_{i=1}^N\left(\log \frac{1}{\sqrt{2 \pi}}-\frac{\left(y_i-w^T x_i\right)^2}{2 \sigma^2}\right) \\ & =\underset{w}{\operatorname{argmax}} \sum_{i=1}^N-\frac{\left(y_i-w^T x_i\right)^2}{2 \sigma^2} \\ & =\underset{w}{\operatorname{argmin}} \sum_{i=1}^N\left(y_i-w^T x_i\right)^2 \\ & =\underset{w}{\operatorname{argmin}} \sum_{i=1}^N\left\|w^T x_i-y_i\right\|_2^2 \\ & \text { (最小二乘法) } \\ & \end{gathered}

可以看到最小二乘法与噪声为高斯噪声时的极大似然估计法是等价的。

五、线性回归的正则化

高维小样本的问题

\hat{w}=\left(X^T X\right)^{-1} X^T Y

当样本数 $N$ 远大于维度 $p$ 时 $X^{T}X$ 可逆，而当出现高维小样本的情况即维度 $p$ 大于样本数 $N$ 时， $X^{T}X$ 就不可逆，这种时候就容易出现过拟合的情况。

处理过拟合的方法面对上述过拟合的现象有一些解决方案，主要有 $\left\{\begin{array}{c}\text { 增加数据量 } \\ \text { 特征选择/特征提取 } \\ \text { 正则化 }\end{array}\right.$

特征选择指的是根据某种规则去掉一些特征来实现降维；特征提取的方法例如主成分分析 (PCA)，也是实现降维；正则化的方法指给损失函数添加惩罚项来避免过拟合。

正则化的方法通过最小化 $J(w)=\frac{L(w)}{\text { loss }}+\frac{\lambda P(w)}{p e n a l t y}$ 来实现正则化，主要有L1正则化和L2正则化（也叫岭回归、权重衰减)。

\left\{\begin{array}{l} \text { L1正则化 }(\text { Lasso }): P(w)=\|w\|_1 \\ \text { L2正则化 }(\text { Ridge }): P(w)=\|w\|_2^2 \end{array}\right.

下面为L2正则化的求解过程:

\begin{gathered} J(w)=L(w)+\lambda P(w) \\ =\left(w^T X^T-Y^T\right)(X w-Y)+\lambda w^T w \\ =w^T X^T X w-2 w^T X^T Y+Y^T Y+\lambda w^T w \\ =w^T\left(X^T X+\lambda I\right) w-2 w^T X^T Y+Y^T Y \\ \hat{w}=\underset{w}{\operatorname{argmin} J}(w) \\ \frac{\partial J(w)}{\partial w}=2\left(X^T X+\lambda I\right) w-2 X^T Y=0 \\ \hat{w}=\left(X^T X+\lambda I\right)^{-1} X^T Y \end{gathered}

半正定矩阵 $X^T X$ 加上对角矩阵 $\lambda I$ 一定是可逆的，可以解决 $X^T X$ 可能不可逆带来的问题。

六、最小二乘法与最大后验估计

已知

仍然认为实际值与估计值之间的差是一个高斯噪声，即 $y$ 和 $f(w)$ 满足关系:

$y=f(w)+\varepsilon=w^T x+\varepsilon \\ 其中 \varepsilon 是高斯噪声, 满足 \varepsilon \sim N\left(0, \sigma^2\right)\\ 因此 y \mid x ; w \sim N\left(w^T x, \sigma^2\right), 即 P(y \mid x ; w)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{\left(y-w^T x\right)^2}{2 \sigma^2}\right\}$

另外假设参数 $w$ 服从先验分布:

w \sim N\left(0, \sigma_0^2\right) \text {, 即 } P(w)=\frac{1}{\sqrt{2 \pi} \sigma_0} \exp \left\{-\frac{\|w\|_2^2}{2 \sigma_0^2}\right\}\\ 后验概率为 P(w \mid Y)=\frac{P(Y \mid w) P(w)}{P(Y)} (这里的 Y 指 Y \mid X, 为书写简单而省略。)

最大后验估计法求解参数 $w$

\begin{gathered} \hat{w}=\underset{w}{argmax}P(w|Y)\\ =\underset{w}{argmax}\frac{P(Y|w)P(w)}{P(Y)}\\ =\underset{w}{argmax}P(Y|w)P(w)\\ =\underset{w}{argmax}\, logP(Y|w)P(w)\\ =\underset{w}{argmax}\, log\prod_{i=1}^{N}P(y_{i}|w)P(w)\\ =\underset{w}{argmax}\sum_{i=1}^{N}logP(y_{i}|w)P(w)\\ =\underset{w}{argmax}\sum_{i=1}^{N}log(\frac{1}{\sqrt{2\pi }\sigma}\frac{1}{\sqrt{2\pi }\sigma_{0}}exp\left \{-\frac{(y-w^{T}x)^{2}}{2\sigma ^{2}}-\frac{\left \| w\right \|_{2}^{2}}{2\sigma _{0}^{2}}\right \})\\ =\underset{w}{argmax}\sum_{i=1}^{N}(log\frac{1}{\sqrt{2\pi }\sigma}\frac{1}{\sqrt{2\pi }\sigma_{0}}+log\, exp\left \{-\frac{(y-w^{T}x)^{2}}{2\sigma ^{2}}-\frac{\left \| w\right \|_{2}^{2}}{2\sigma _{0}^{2}}\right \})\\ =\underset{w}{argmax}\sum_{i=1}^{N}(-\frac{(y-w^{T}x)^{2}}{2\sigma ^{2}}-\frac{\left \| w\right \|_{2}^{2}}{2\sigma _{0}^{2}})\\ =\underset{w}{argmin}\sum_{i=1}^{N}(\frac{(y-w^{T}x)^{2}}{2\sigma ^{2}}+\frac{\left \| w\right \|_{2}^{2}}{2\sigma _{0}^{2}})\\ =\underset{w}{argmin}\sum_{i=1}^{N}(\underset{LSE}{\underbrace{(y-w^{T}x)^{2}}}+\underset{\lambda }{\underbrace{\frac{\sigma ^{2}}{\sigma _{0}^{2}}}}\left \| w\right \|_{2}^{2}) \end{gathered}

可以看到正则化的最小二乘法与噪声为高斯噪声且先验也是高斯分布时的最大后验估计法是等价的。

七、总结

L S E \Leftrightarrow M L E \text { (noise为Gaussian Distribution) }\\ Regularized LSE \Leftrightarrow M A P (noise、prior 为Gaussian Distribution)

线性回归模型是最简单的模型，但是麻雀虽小，五脏俱全，在这里，我们利用最小二乘误差得到了闭式解。同时也发现，在噪声为高斯分布的时候，MLE 的解等价于最小二乘误差，而增加了正则项后，最小二乘误差加上 L2 正则项等价于高斯噪声先验下的 MAP解，加上 L1 正则项后，等价于 Laplace 噪声先验。

传统的机器学习方法或多或少都有线性回归模型的影子：

线性模型往往不能很好地拟合数据，因此有三种方案克服这一劣势：
1. 对特征的维数进行变换，例如多项式回归模型就是在线性特征的基础上加入高次项。
2. 在线性方程后面加入一个非线性变换，即引入一个非线性的激活函数，典型的有线性分类模型如感知机。
3. 对于一致的线性系数，我们进行多次变换，这样同一个特征不仅仅被单个系数影响，例如多层感知机（深度前馈网络）。
线性回归在整个样本空间都是线性的，我们修改这个限制，在不同区域引入不同的线性或非线性，例如线性样条回归和决策树模型。
线性回归中使用了所有的样本，但是对数据预先进行加工学习的效果可能更好（所谓的维数灾难，高维度数据更难学习），例如 PCA 算法和流形学习。

『白板推导系列笔记』3.线性回归