动态规划：

正向完善 dp 会发现之后的情况会影响之前的情况，所以我们从终点出发，逆向推到动态转移
构造 dp[i][j] 表示到当前格到终点所需要的最小健康点数
方便写代码，我们多开了一行一列
我们将无法到达的区域置为无穷大，其实也就是最后一行和最后一列，这里我们将全部值都初始化为了无穷大，只是这样写更方便，且并不会影响结果
无穷大是为了让 dp 转移取决于另一个有效值
但 dp[n][m] 状态转移来自两个无效值，所以将这两个值做特殊处理
最后状态转移，返回dp[0][0]即可

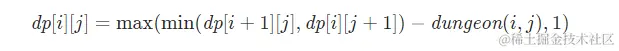
func calculateMinimumHP(dungeon [][]int) int {
    n, m := len(dungeon), len(dungeon[0])
    dp := make([][]int, n + 1)
    for i := 0; i < len(dp); i++ {
        dp[i] = make([]int, m + 1)
        for j := 0; j < len(dp[i]); j++ {
            dp[i][j] = math.MaxInt32
        }
    }
    dp[n][m - 1], dp[n - 1][m] = 1, 1
    for i := n - 1; i >= 0; i-- {
        for j := m - 1; j >= 0; j-- {
            minn := min(dp[i+1][j], dp[i][j+1])
            dp[i][j] = max(minn - dungeon[i][j], 1)
        }
    }
    return dp[0][0]
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

未优化版本

func calculateMinimumHP(on [][]int) int {
    n := len(on)
    m := len(on[0])
    dp := make([][]int, n)
    for i := range dp{
        dp[i] = make([]int, m)
    }
    dp[n-1][m-1] =  max(1, -on[n-1][m-1] + 1)
    for i := n-2; i >= 0; i-- {
        dp[i][m-1] = max(1, max(dp[i+1][m-1] - on[i][m-1], -on[i][m-1] + 1))
    }
    for j := m-2; j >= 0; j-- {
        dp[n-1][j] = max(1, max(dp[n-1][j+1] - on[n-1][j], -on[n-1][j] + 1))
    }
    for i := n-2; i >= 0; i-- {
        for j := m-2; j >= 0; j-- {
            dp[i][j] = max(1, max(min(dp[i+1][j], dp[i][j+1]) - on[i][j], -on[i][j] + 1))
        }
    }
    return dp[0][0]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

地下城游戏——动态规划

动态规划：

未优化版本