本文作者:伍友良,欢迎添加作者私人微信(wylpri)告诉他你所知道的有趣信息。
前言
作者感染新冠后或有脑雾,加之本文编写仓促,可能有错漏,见谅。
我们研究的手段是使用概率学。
先说点小学毕业就能懂的。
核酸检测是有准确率的,这个准确率不为100%。这个好理解。
我们假设准确率是99%,这个准确率已经算很高了。
现在有10亿民众参与核酸检测,他们都没有感染新冠,那么大概会有10,000,000(1%*1,000,000,000)个人被检测为核酸阳性。厉害了,一千万个人检测为阳性!
我们是讲究科学的,对于阳性的一千万人,我们会组织第二次检测,即使如此,仍然大致会有10万人二次检测为阳性。
两次为阳性,那没说的,单独隔离起来,或者送到方舱集中隔离。
接下来会发生什么?这些人本来就没有新冠,自然是好的很,没有任何症状,能吃能喝能睡,还能——跳舞。
专家此时可能会在小本上记:感染新冠的10万人,100%无症状。
呵呵,上述结论已经违反科学了。
我们继续往下分析。
贝叶斯定理
樊登的爸爸感染新冠后去世了,他写了一篇文章《我的爸爸凌晨走了》,其中写到:
是我们选择没有做有创抢救,他不喜欢痛苦。
爸爸昨天昏迷时还在空中比划做数学题。我叫醒他,他说“这是个贝叶斯分布。”
樊老教授可能已经发现了专家说法不靠谱的根本原因:专家计算时没有考虑概率问题。
其实使用贝叶斯定理,可以解释:
为什么之前专家感染新冠95%无症状,而防疫放开后,我们发现,95%有症状还差不多。
贝叶斯定理,或者说贝叶斯公式是这样的:
P(A∣B)=P(A)P(B)P(B∣A)
这个公式,讲了个什么道理呢?
我们还是用大白话来解读:
B事件出现时,A事件的概率会大大提高。
用图来表示就是:
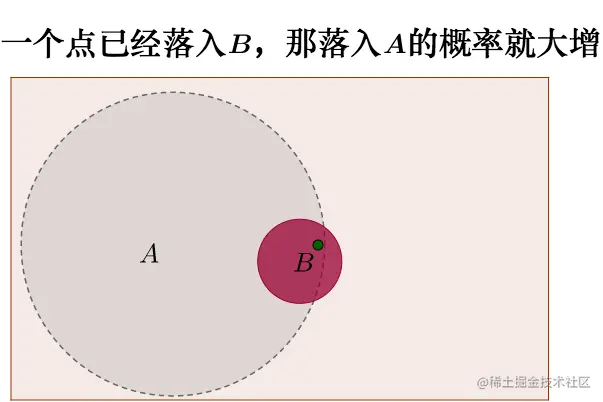
贝叶斯图示(来源:https://www.matongxue.com/)
使用贝叶斯定理解释有症状的概率问题
先将一些事件用字母来表示:
A:核酸检测为阳性
B:已经感染新冠
A′:核酸检测为阴性
B′:未感染新冠
再假设,核酸检测准确率为99%,即有:
P(A|B)=99%,这个是指已经感染新冠被检测为阳性的概率;
P(A'|B')=99%,这个是指未感染新冠被检测为阴性的概率。
假设没有人感染新冠
此时P(B)=0。我们算算核酸检测为阳性,实际也确实感染新冠的概率:
P(B∣A)=P(B)P(A)P(A∣B)=0
这简直有点像废话,直觉就能告诉我,没有人感染情况下,核酸检测为阳性,感染新冠的概率仍然为0。
没有感染新冠自然也没有症状。
假设有1‰的人感染新冠
此时P(B)=1‰。我们仍然要算的是核酸检测为阳性,实际也确实感染新冠的概率:
P(B∣A)=P(B)P(A)P(A∣B)
P(A)=P(B)∗P(A∣B)+P(B′)∗P(A∣B′),用白话解读就是,感染新冠且被检测出阳性的概率+未感染新冠且被检测出阳性的概率。
P(A∣B′)=1−P(A′∣B′)=1−99%=1% 解释:未感染新冠但核酸为阳性的概率=1-未感染新冠且核酸为阴性的概率
P(B∣A)=P(B)P(A)P(A∣B)=P(B)P(B)∗P(A∣B)+P(B′)∗P(A∣B′)P(A∣B)
=1‰1‰∗99%+999‰∗1%99%=9.0164%
这个情况下,大部分阳性人员实际未感染新冠。
假设感染新冠有症状的概率实际为95%,但是此时统计观察到的有症状的人员占所有阳性人员的比例(后文简称有症状比例)却只有9.0164%∗95%≈8.5656%。
假设有1%的人感染新冠
此时P(B)=1%。
P(B∣A)=P(B)P(A)P(A∣B)=P(B)P(B)∗P(A∣B)+P(B′)∗P(A∣B′)P(A∣B)
=1%1%∗99%+99%∗1%99%=50%
假设感染新冠有症状的概率实际为95%,此时统计观察到的有症状比例为50%∗95%=47.5%
假设有50%的人感染新冠
此时P(B)=50%。
P(B∣A)=P(B)P(A)P(A∣B)=P(B)P(B)∗P(A∣B)+P(B′)∗P(A∣B′)P(A∣B)
=50%50%∗99%+50%∗1%99%=99%
假设感染新冠有症状的概率实际为95%,此时统计观察到的有症状比例为99%∗95%=94.05%
小结
通过上述分析,我们发现:
- 当实际感染比例特别低时,统计观察到的有症状比例远低于实际比例。这个时候专家可能得出有症状比例很低的错误结论。
- 当实际感染比例上升时,统计观察到的有症状比例迅速接近实际有症状比例。这个时候我们会发现专家的说法非常不靠谱。
参考资料
樊登:我爸爸凌晨走了_腾讯新闻 (qq.com)
如何理解贝叶斯定理?