本文章参考了Lilian Weng的《From GAN to WGAN》这篇文章，原文链接《From GAN to WGAN》,可以去看看

KL散度和JL散度

在机器学习中，常常用KL散度（Kullback-Leibler Divergence）和JL散度(Jensen-Shannon Divergence)来衡量两个分布的近似程度

KL散度

KL散度是用来，评价p与目标分布q之间的相似程度

D_{KL}(p||q) = \sum_{x \in X}p(x)log \frac{p(x)}{q(x)}

通过这个公式，我们可以知道，KL散度越大，代表着q(x)表达p(x)的能力越差
当p(x)与q(x)完全相同时, $D_{KL} = 0$ ，且KL散度不具有对称性

JS散度是对称的，取值在0到1。如果两个分布完全没有重叠，此时KL散度是完全没有意义的，也就意味着这一点梯度为0，这时就需要JS散度

D_{JS}(p||q) = \frac{1}{2}D_{KL}(p||\frac{p+q}{2}) + \frac{1}{2}D_{KL}(q||\frac{p+q}{2})

JS散度更为平滑，GAN取得成功背后的一个原因是将传统最大似然估计中不对称的KL散度改为对称的JS散度。

Wasserstein距离还有一个名字叫推土机距离，这是因为计算Wasserstein距离的过程跟推土填土的过程很像。
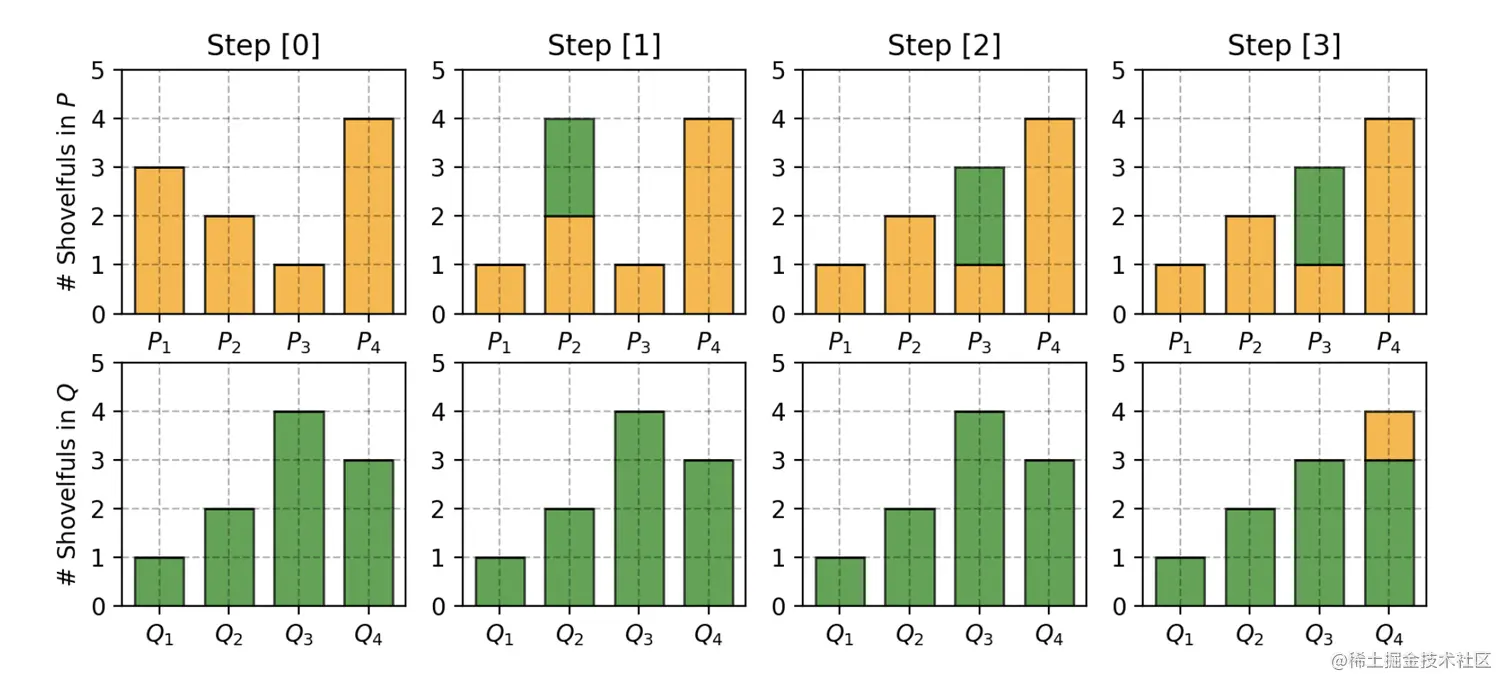
让我们来看一个很简单的例子，假设有两个分布P和Q，P和Q共有4堆泥土

P_1 = 3,P_2 = 2, P_3 = 1, P_4 = 1

Q_1 = 1, Q_2 = 2, Q_3 = 4, Q_4 = 3

两个分布相等的意思，就是 $P_1$ 和 $Q_1$ 相等, $P_2$ 和 $Q_2$ 相等,依此类推。我们逐个观察。

代价计算函数为 $\delta_{i+1} = \delta_i + P_{i} - Q_{i}$ 。在这个例子中

\begin{aligned} \delta_0&= 0 \\ \delta_1&= 0 + 3 - 1 = 2 \\ \delta_2&= 2 + 2 - 2 = 2 \\ \delta_3&= 2 + 1 - 4 = -1 \\ \delta_4&= -1 + 4 - 3 = 0 \\ \end{aligned}

最终的Wasserstein距离 $W = \sum ｜\delta_i｜= 5$

截屏2022-12-27 上午11.39.19.png

即使两个分布在低维且分布之间没有重叠，Wasserstein距离仍然有意义且可以平滑的表示两者之间的距离。