向量

向量既有长短又有方向，在 WebGL 中，向量可以代表一段位移，可以表示光照的角度等。

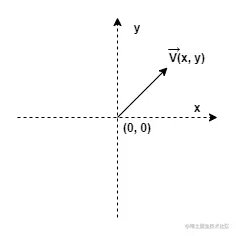
坐标系1.png

向量长度

向量长度公式如下所示：

\vec v 的长度 = \sqrt {x^2 + y^2}

单位向量

单位向量是长度为 1 的向量，对于大部分向量，我们只关心向量的方向，而不在意向量的长度，这种情况下就适合用单位向量来表示。比如光线入射方向、反射方向等向量，单位向量通常也被称为标准向量。

向量的加（减）法

下图是两个向量相加的一个示意图，其意义为将向量 v1 的终点 (x1, y1)，沿着向量 v2 的方向移动一段距离，这段距离的长度为 v2 向量的长度。

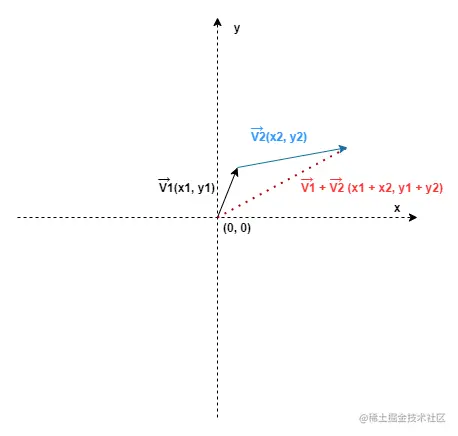
坐标系2.png

向量加法公式如下：

\vec {v1} + \vec {v2} = (x1 + x2, y1 + y2)

维度相同的两个向量才可以相加或者相减，得到的新向量维度和原向量相同，新向量各个分量等于原向量各个分量之和或之差。
向量不能和标量相加。
向量减法不满足交换律。
向量加法满足交换律。

向量伸缩

向量伸缩即向量乘上一个标量，公式如下所示：

\vec v = (x, y) \\ n\vec v = (nx, xy)

向量旋转

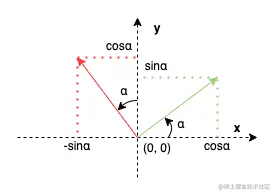
可视化3.png

这里可能需要一点矩阵的知识，列出旋转矩阵如下：

\begin{bmatrix} x\\ y\\ \end{bmatrix} \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \\ \end{bmatrix} = \begin{bmatrix} x \cos \alpha - y \sin \alpha \\ x \sin \alpha + y \cos \alpha \\ \end{bmatrix}

向量旋转公式如下：

\vec v 旋转 \alpha 度之后的坐标 = (x \cos \alpha - y \sin \alpha, x \sin \alpha + y \cos \alpha)

向量点乘

向量点乘就是将两个向量的各个分量的乘积相加，返回一个标量。在光照模型中，漫反射光照强度因子就是光照入射角度与法向量的余弦值（单位化后）。

向量点乘公式如下：

\vec a = (a1, a2) \\ \vec b = (b1, b2) \\ \vec a \bullet \vec b = a1b1 + a2b2

其数学上含义为向量 b 在向量 a 上的投影的长度与向量 a 的长度相乘，两个向量之间的夹角为 α，所以下面这个公式也成立：

\vec a \bullet \vec b = |\vec a||\vec b| \cos \alpha

向量叉乘

二维向量 a 和 b 的叉积为向量 a 与向量 b 沿垂直方向的投影的乘积，其几何意义就是向量 a、b 组成的平行四边形的面积，注：二维空间无法得到一个和原向量组成的坐标平面垂直的新向量，所以只能求出乘积的标量。

| \vec a × \vec b | = |\vec a||\vec b| \sin \alpha

二维空间中向量叉乘的物理意义是 a 和 b 两个力的力矩，力矩可以理解为一个物体在力的作用下，绕着一个轴转动的趋向。它是一个向量，等于力臂 L 和力 F 的叉乘。

\vec a × \vec b =(x1, y1) × (x2, y2) = \begin{bmatrix} x1 & y1 \\ x2 & y2 \\ \end{bmatrix} = x1y2 - x2y1

事实上，向量叉乘的运算结果不是标量而是一个向量，一般用于3D坐标系中，且叉乘得到的新向量与两个原向量组成的坐标平面垂直。

\vec a = (x1, y1, z1) \\ \vec b = (x2, y2, z2) \\ \vec a × \vec b = (y1z2 - y2z1, x2z1 - x1z2, x1y2 - x2y1)

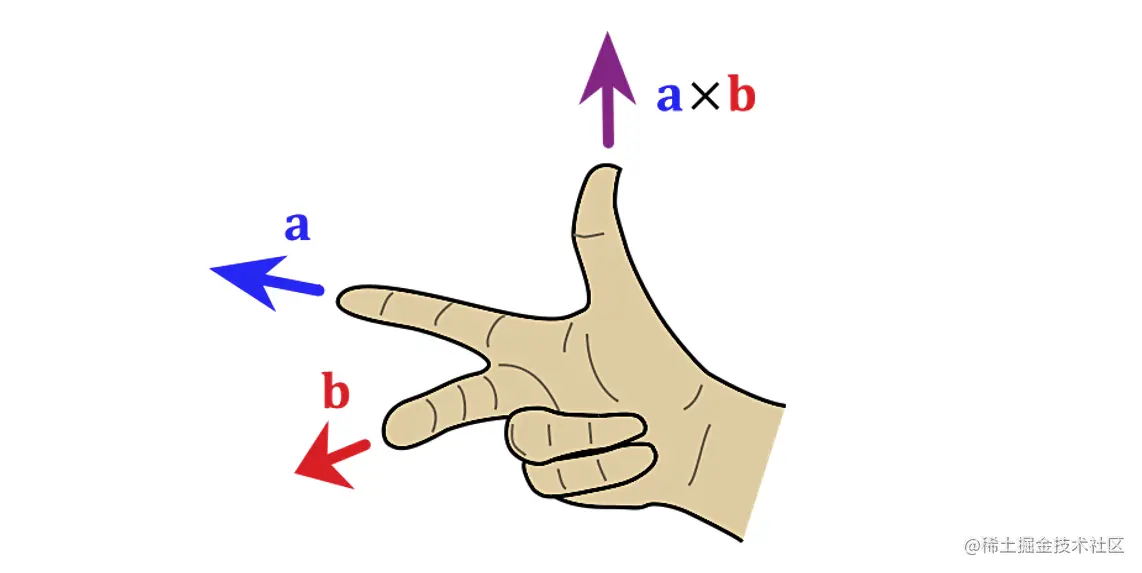
确定出 a、b 的叉积方向的方法：x 轴向右、y 轴向下的坐标系是右手系。在右手系中求向量 a、b 叉积的方向时，我们可以把右手食指的方向朝向 a，把右手中指的方向朝向 b，那么大拇指所指的方向就是 a、b 叉积的方向，这个方向是垂直纸面向外（即朝向我们）。因此，右手系中向量叉乘的方向就是右手拇指的方向，那左手系中向量叉乘的方向自然就是左手拇指的方向了。

矩阵

矩阵是按照行列排列的一系列数值得的集合，一个矩阵通常是由 m 行 n 列组成，我们称之为 m x n 矩阵，如果 m 和 n 相同，该矩阵代表一个方阵。

在 WebGL 中，前面讲的向量也可以用矩阵来表示，横着写1行4列为行向量，竖着写4行1列为列向量。

矩阵加减

两个矩阵相加或者相减需要满足一个条件，即两个矩阵必须同型，同型的意思是，行数和列数都必须一样。一个 m x n 矩阵和一个 n x m 矩阵（m 不等于 n ）是不能进行加减的。

\begin{bmatrix} a1 & a2 \\ a3 & a4 \\ \end{bmatrix} + \begin{bmatrix} b1 & b2 \\ b3 & b4 \\ \end{bmatrix} = \begin{bmatrix} a1+b1 & a2+b2 \\ a3+b3 & a4+b4 \\ \end{bmatrix}

矩阵乘法

矩阵既可以和标量相乘，也能和矩阵相乘，也能和向量相乘。在讲解乘法运算之前，我们必须先明确相乘的顺序，因为矩阵相乘不满足交换律。

矩阵和标量相乘，返回一个新矩阵，新矩阵的各个元素等于原矩阵各个元素与标量的乘积。

\begin{bmatrix} a1 & a2 \\ a3 & a4 \\ \end{bmatrix} × c = \begin{bmatrix} ca1 & ca2 \\ ca3 & ca4 \\ \end{bmatrix}

矩阵与矩阵相乘也要满足一定条件：矩阵M×矩阵N，矩阵M的列数需要等于矩阵N的行数。

\begin{bmatrix} a1 & a2 & a3 \\ a4 & a5 & a6\\ \end{bmatrix} × \begin{bmatrix} b1 & b2 \\ b3 & b4 \\ b5 & b6 \\ \end{bmatrix} = \begin{bmatrix} a1b1 + a2b3 + a3b5 & a1b2 + a2b4 + a3b6 \\ a4b1 + a5b3 + a6b5 & a4b2 + a5b4 + a6b6 \\ \end{bmatrix}

转置矩阵

矩阵转置就是将原来矩阵的行向量转变为列向量，假设有一个矩阵M：

M = \begin{bmatrix} a1 & a2 \\ a3 & a4 \\ \end{bmatrix}

其转置矩阵为：

M^T = \begin{bmatrix} a1 & a3 \\ a2 & a4 \\ \end{bmatrix}

逆矩阵

假设有一个 m 阶方阵A（A 矩阵必须是方阵才可能有逆矩阵），如果存在一个 n 阶方阵B，使得 A x B = B x A = I，其中 I 是单位矩阵，那么 B 是 A 的逆矩阵。A 矩阵是可逆矩阵，也称为非奇异矩阵，矩阵 A 的逆矩阵用 A 的 -1 次方表示。

A的逆矩阵 = A^{-1}

单位矩阵，以三阶为例：

I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}

逆矩阵在 WebGL 中的，有着非常重要的意义，将一个变换矩阵左乘一个列向量（此处列向量代表顶点坐标），代表了对原始顶点执行了某种变换，比如：旋转、缩放、平移等。逆矩阵的意义就是能够撤销这种变换，将变换后的坐标再还原回去。

实例：变换矩阵M，顶点坐标向量P，变换后的矩阵P1，先用M对P进行变换，然后再撤销这个变换，可以表达为下面的公式：

P_1 = M × P \\ P = M^{-1} × P_1

推导过程：

P = P × I = P × M × M^{-1} = P_1 × M^{-1}

逆矩阵求解方法

正交矩阵

方阵M，当且仅当与其转置矩阵的乘积等于单位矩阵时，称其为正交矩阵。

M × M^T = I

根据前面逆矩阵的定义不难得出，其转置矩阵和逆矩阵是相等的，即：

M^T = M^{-1}

正交矩阵的一个好处是，如果一个矩阵是正交矩阵，那么计算它的逆矩阵时，只需要对原矩阵转置即可，从而减少了计算量（逆矩阵的求解过程是很繁琐的），3D图形学中的最常见的旋转和镜像变换就都是用的正交矩阵实现的。

正交矩阵的判断条件：

矩阵的每一行都是单位向量
矩阵的某一行与其它行向量互相垂直，点积为0

WebGL 基础 - 3D数学

向量