《线性代数的本质》学习笔记

诸神缄默不语
335 阅读11分钟

开启掘金成长之旅！这是我参与「掘金日新计划 · 12 月更文挑战」的第13天

本文首发于CSDN。

诸神缄默不语-个人CSDN博文目录

本文是3B1B视频课程《线性代数的本质》全内容笔记。

@TOC

原视频：【官方双语/合集】线性代数的本质 - 系列合集

1. 向量vector

  1. 向量是什么
    1. 物理视角：箭头 （长度和方向决定一个向量）
    2. 计算机视角：有序数字列表
    3. 数学视角：可以进行相加或数乘的一切
    4. （直观视角：各方向运动的合成/对某一方向的运动）
  2. 在线性代数中，向量常常以原点作为起点
  3. 列表视角与箭头视角的关联：通过向量坐标（每个值是沿着对应轴走多远）
  4. 向量相加：三角形定理
    1. 运动视角：进行两个向量的运动
    2. 数字视角：加和各坐标系值
  5. 数乘：数字（标量scalar）的作用是缩放（scale）向量
    1. 向量整体缩放，相当于分量缩放（对以列表视角看向量相当于每个数被乘）

2. 线性组合、线性生成空间与基

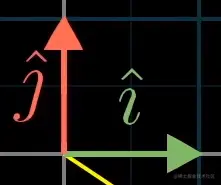  1. 在这里插入图片描述 基向量，坐标系的基 向量坐标，可以视作：用各数字分别缩放基向量，再将其缩放后的向量相加： ai→+bj→a\overrightarrow{i}+b\overrightarrow{j} 事实上，我们可以选择别的基，构成另一种坐标系

  2. 标量与向量乘积之和的结果，被称为这些向量的线性组合：av→+bw→a\overrightarrow{v}+b\overrightarrow{w} 所有结果组成一个集合，这个集合给称为这些向量的张成空间span 在二维平面，就是全部的线组成平面/还是一根线

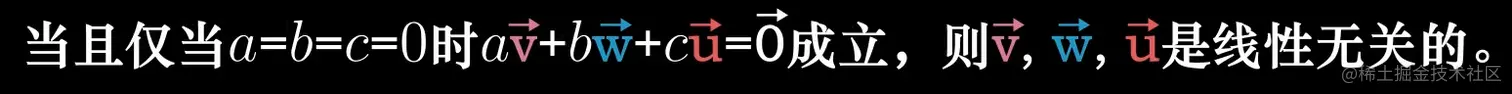
  3. 在一组向量中，至少有一个是多余的，没有对张成空间做出任何贡献 or 移除一个向量，不影响生成空间 ⇒\Rightarrow线性相关 or 其中一个向量可以被表示为其他向量的线性组合，因为这个向量已经落在其他向量张成的空间之中   反之则为线性无关 使所有向量地位平等的定义法： 在这里插入图片描述

  4. 空间的一组基：张成该空间的一个线性无关向量的集合

3. 矩阵与线性变换

  1. 线性代数中，变换是一个向量变化为另一个向量的函数   线性变换
    1. 直线在变换后仍然保持为直线，且原点固定
    2. “保持网格线平行并等距分布”的变换
  2. 如何数学地描述空间上所有向量的线性变换：
  3. 记录i^\widehat{i}和j^\widehat{j}的变化 向量变化前后是基向量的同一个线性组合 缩放基向量后再用这个线性组合计算向量：
    [abcd]⋅[xy]=x[ac]+y[bd]=[ax+bycx+dy]\begin{bmatrix} a & b \\ c & d \end{bmatrix}\cdot \begin{bmatrix} x \\ y \end{bmatrix}=x\begin{bmatrix} a \\ c \end{bmatrix}+ y\begin{bmatrix} b \\ d \end{bmatrix}=\begin{bmatrix} ax+by \\ cx+dy \end{bmatrix}   [abcd]\begin{bmatrix} a & b \\ c & d \end{bmatrix}是基向量变换后的坐标（第一列是第一个基向量）
    [xy]\begin{bmatrix} x \\ y \end{bmatrix}是原坐标系中的向量
  4. 剪切shear[1101]\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}
  5. 变换：也有列向量之间线性相关这种情况
  6. 若一个变换L满足以下两条性质：
    L(v→+w‾)=L(v→)+L(w→)(1)可加性L(cv‾)=cL(v→)(2)成比例（一阶齐次）\begin{aligned} L\left( \overrightarrow{v}+\overline{w}\right) &=L\left( \overrightarrow{v}\right)+L\left( \overrightarrow{w}\right) &&(1)可加性\\ L\left( c\overline{v}\right) &=cL\left( \overrightarrow{v}\right) &&(2)成比例（一阶齐次）\\ \end{aligned}
    则称L是线性的

4. 矩阵乘法与线性变换复合

  1. 两个独立变换的“复合变换”：先变换一次，再变换一次 ↓ 乘积 需要从右向左读：先应用右边矩阵表示的变换，再应用左边的变换 一个矩阵，一个交换

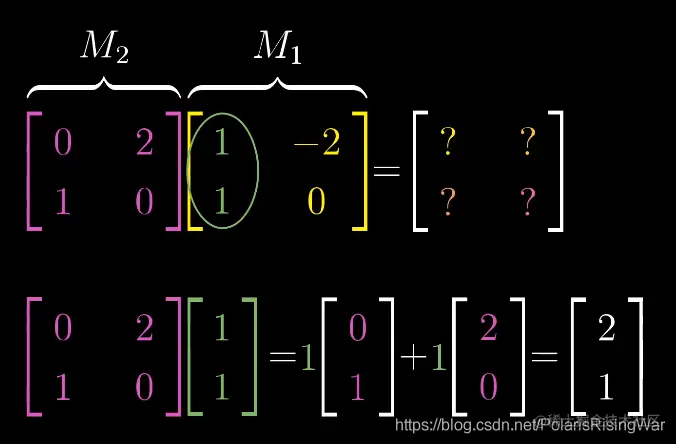
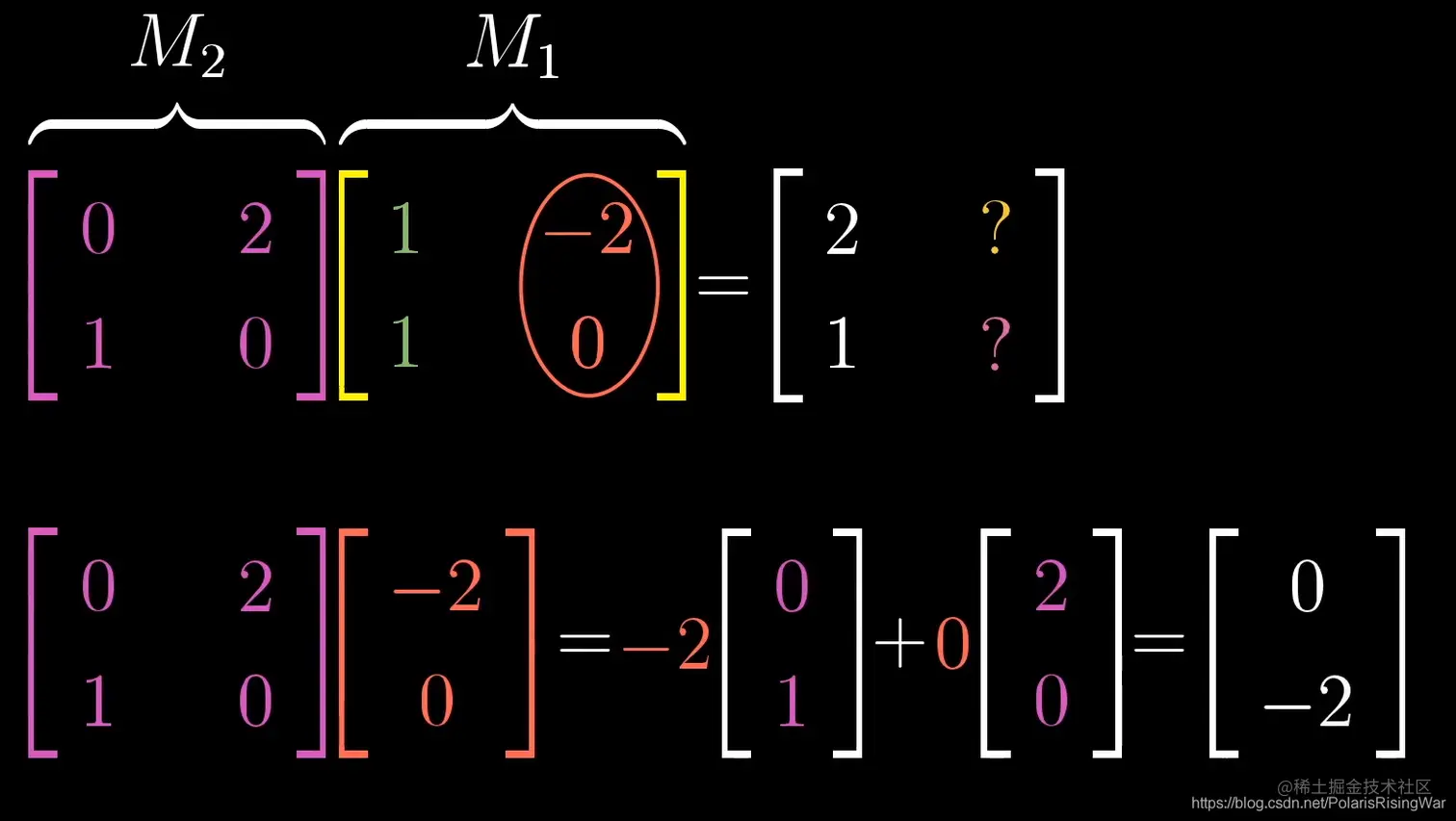
  2. 依然可以视作基向量的变换： 在这里插入图片描述 在这里插入图片描述

  3. 不能交换，可以结合

  4. 附注：三维线性变换 i→\overrightarrow{i} j→\overrightarrow{j} k→\overrightarrow{k}   [.........]\begin{bmatrix} . & . & . \\ . & . & . \\ . & . & . \end{bmatrix}

5. 行列式determinant

  1. 行列式，用于测量矩阵（变换）扩大/挤压的程度⇒\Rightarrow测量一个给定区域面积增大或减小的比例 可以用原空间的一个 (1,1) 小格子来进行直观理解

  2. 行列式为0，代表这个矩阵（变换）将空间压缩到更小的维度上 （列的线性相关）

  3. 翻转平面，orientation of space转变了：行列式为负

  4. 三维行列式：变换形成的平行六面体的体积 空间方向：右手定则（如果变换后需要用左手，行列式为负）

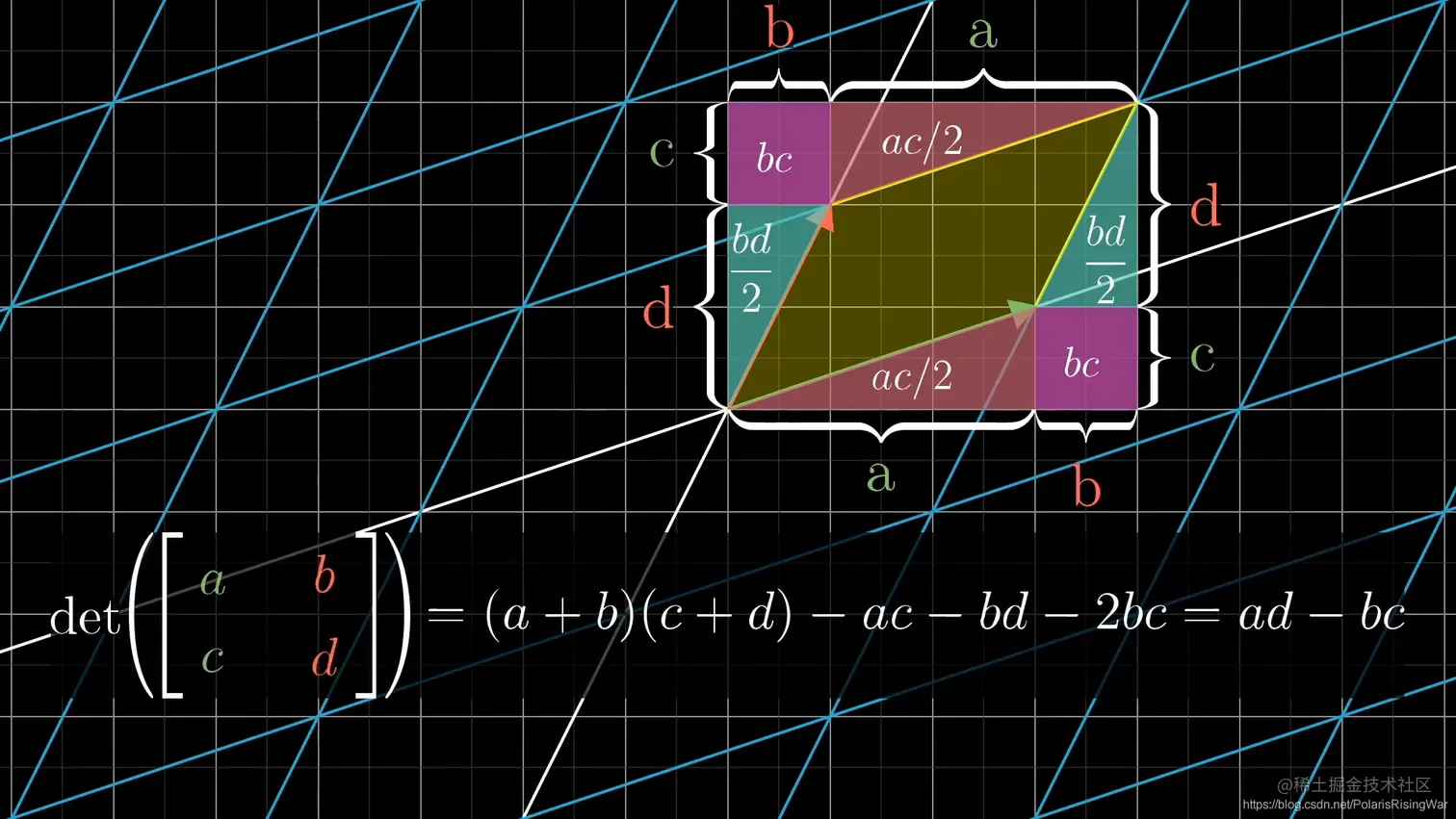
  5. 行列式计算公式： 在这里插入图片描述

  6. det(M1M2)=det(M1)⋅det(M2)det(M_{1}M_{2})=det(M_{1})\cdot det(M_{2})

6. 逆矩阵、列空间与零空间、秩

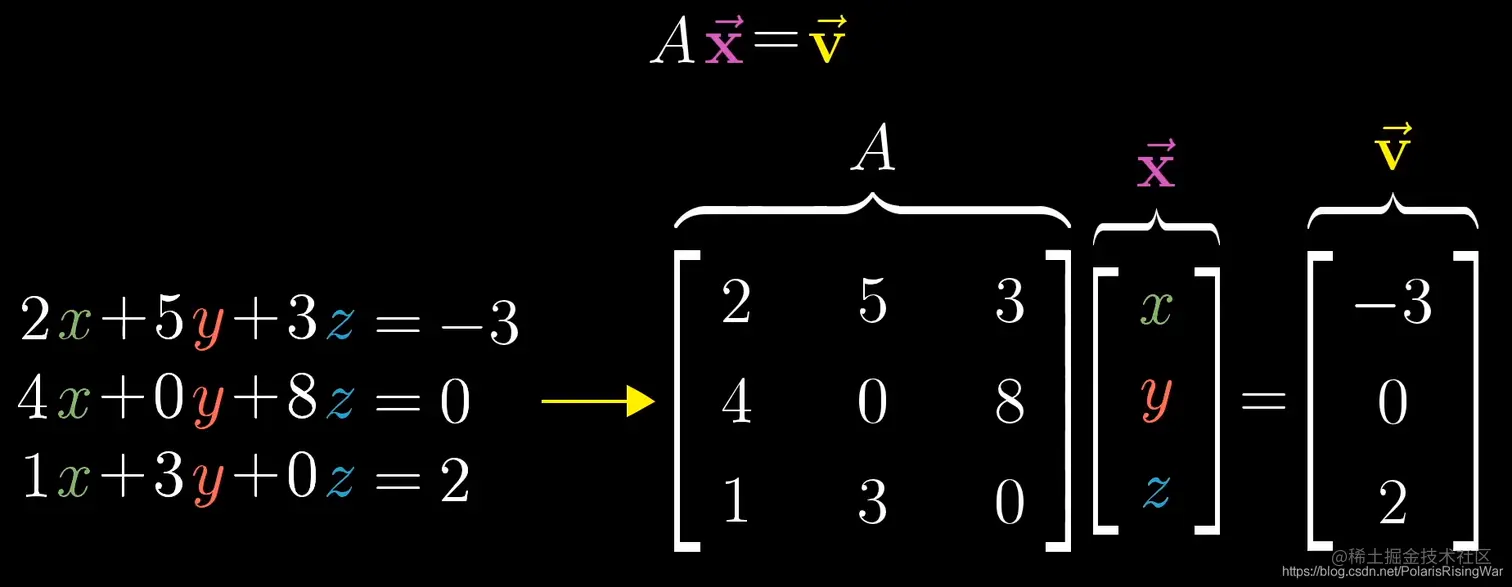
  1. 线性方程组 系数矩阵A 在这里插入图片描述
  2. 逆矩阵 如果变换没有将空间降维，那么v总是有一个x能与之对应。计算方法是使Ax→=v→A\overrightarrow{x}=\overrightarrow{v}此式左乘A−1A^{-1} 直觉理解：用一个逆变换（逆矩阵）复原变换 即A−1A=IA^{-1}A=I 是一个恒等变换（什么都不做）
  3. det(a)≠0⇒A−1det(a)\neq0\Rightarrow A^{-1}存在
  4. det(a)=0⇒det(a)=0\Rightarrow在经过这个变换压缩后，没法通过线性变换升维（用一个逆矩阵复原），也就是不存在A−1A^{-1}（如果v→\overrightarrow{v}在这个低维空间上，方程组就有解，不在就无解）
  5. 有些行列式为0的矩阵变换将空间压缩得更狠（有些压成线，更狠的压成点） 秩：衡量压缩程度
    1. 变换后空间的维数（压缩程度）
    2. 列空间的维数
  6. A的列空间
    1. 所有可能的输出向量Av→A\overrightarrow{v}构成的集合
    2. 矩阵的列所张成的空间
    3. 零向量一定会被包含在列空间中
    4. 它可以告诉我们什么时候存在解
  7. 满秩
  8. 矩阵的零空间或核：在变换后落在原点的向量集合
  9. 原视频未提到计算方面内容，建议搜索相应关键词学习：高斯消元法、行阶梯型
  10. 附注2：非方阵：可看作是输入输出维数不同的线性变换 和方阵的一样，每列向量是基向量变换后的坐标

7. 点积与对偶性

  1. 点积
    1. 观点1：向量对应位元素相乘，对其求和
    2. 观点2：长度×正交投影长度 如果两个向量垂直，点积：0 点积与顺序无关的直觉解释：如果两个向量等长，那么按照对称性，两个投影应该也一样长，两个投影-长度乘积互为镜像；如果两个向量不等长，可以将其想象为两个等长向量中的一个按比例伸缩，对面投影到这个上面的长度又不变，这个投影到对面的长度按比例伸缩，所以最后乘起来还是一样的
  2. 对偶性：两种数学事物之间自然而又出乎意料的对应关系 解释点积两种观点的统一性
  3. （类似于6的附注2） 多维空间到一维空间（数轴）的线性变换 一个长这样的一维横向量：[ . . ]→矩阵向量乘法（点积） （1个从向量到数的映射）
  4. 将二维向量投影到一条线上的函数：一个线性变换 是点积的观点2 这个线性变换的矩阵是该线上的单位向量v→\overrightarrow{v}的x，y坐标构成的(1,2)矩阵（证明方式：对称性） （所以对单位向量来说，很显然其点积的观点1、2是一致的）（而非单位向量，和1中2的直觉理解逻辑一样，对其进行对应的缩放就行） 也就是点积的观点1 应用这个变换 = 和这个v→\overrightarrow{v}做点积

8. 叉积

  1. v→×w→=向量平行四边形的面积（行列式）\overrightarrow{v}\times\overrightarrow{w}=向量平行四边形的面积（行列式） 方向：符合基向量方向的叉积结果（指顺 i^×j^\widehat{i}\times\widehat{j} 的方向）为正 右手法则，指向纸外的方向为正 注意：将向量写成矩阵的行和写成矩阵的列，都是一样的，因为转置不影响行列式的值 一个矩阵（变换）的行列式，变换后面积扭曲的程度
  2. 真正的叉积：一个新向量，垂直于向量平行四边形 长度是其值 方向判定：右手法则（食指v→\overrightarrow{v}，中指w→\overrightarrow{w}）（对我来说是直接抱圆了，一样的）
  3. [v1v2v3]×[ω1ω2ω3]=det⁡([i^v1ω1j^v2ω2k^v2ω3])=i^(v2ω3−v3ω2)+j^(v3ω1−v1ω3)+k^(v1ω2−v2ω1)\begin{aligned} \begin{bmatrix} v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}\times\begin{bmatrix} \omega _{1} \\ \omega _{2} \\ \omega _{3} \end{bmatrix} &=\det \left( \begin{bmatrix} \widehat{i} & v_{1} & \omega_{1} \\ \widehat{j} & v_{2} & \omega_{2} \\ \widehat{k} & v_{2} & \omega_{3} \end{bmatrix}\right) \\ &=\widehat{i}\left( v_{2}\omega_{3}-v_{3}\omega_{2}\right) + \widehat{j}\left( v_{3}\omega_{1}-v_{1}\omega_{3}\right) + \widehat{k}\left( v_{1}\omega_{2}-v_{2}\omega_{1}\right) \end{aligned}
  4. 以线性变换的眼光看叉积： 对偶性：一个（从空间）到数轴的线性变换（变换矩阵为[ . . ]）→\rightarrow这个变换的对偶向量[...]\begin{bmatrix} . \\ . \\ . \end{bmatrix} 应用线性变换  ⟺  \iff与这个向量做点积 根据v→\overrightarrow{v}和w→\overrightarrow{w}定义一个三维到一维的线性变换⇒\Rightarrow找到它的对偶向量⇒\Rightarrow说明其就是v→×w→\overrightarrow{v}\times\overrightarrow{w} f([xyz])=det⁡([xv1ω1yv2ω2zv3ω3])f\left( \begin{bmatrix} x \\ y \\ z \end{bmatrix}\right) =\det \left( \begin{bmatrix} x & v_{1} & \omega_{1} \\ y & v_{2} & \omega_{2} \\ z & v_{3} & \omega_{3} \end{bmatrix}\right) 一个线性变换 其中det⁡([xv1ω1yv2ω2zv3ω3])\det \left( \begin{bmatrix} x & v_{1} & \omega_{1} \\ y & v_{2} & \omega_{2} \\ z & v_{3} & \omega_{3} \end{bmatrix}\right)是这三个向量构成的平行六面体的体积 这是一个线性变换 f是[…][xyz]→[...].[xyz]\left[ \ldots \right] \begin{bmatrix} x \\ y \\ z \end{bmatrix}\rightarrow \begin{bmatrix} . \\ . \\ . \end{bmatrix} .\begin{bmatrix} x\\ y\\ z\end{bmatrix} [...]\begin{bmatrix} . \\ . \\ . \end{bmatrix}是p p⇒{p1=v2w3−v3w2p2=v3w1−v1w3p3=v1w2−v2w1\Rightarrow \begin{cases}p_{1}=v_{2}w_{3}-v_{3}w_{2}\\ p_{2}=v_{3}w_{1}-v_{1}w_{3}\\ p_{3}=v_{1}w_{2}-v_{2}w_{1}\end{cases}
    1. 在计算上：右边那个行列式最后算出来就是这样的
    2. 在几何上：平行四边形的面积×(x,y,z)\times(x,y,z)在垂直于v→\overrightarrow{v}和w→\overrightarrow{w}方向上的分量=垂直于v→\overrightarrow{v}和w→\overrightarrow{w}且长度为平行四边形的面积的向量⋅[xyz]\cdot\begin{bmatrix} x \\ y\\ z \end{bmatrix}（注意点乘是投影×\times原长，投影过去就是平行六面体的高，原长（p）是平行四边形的面积）

9. 基变换

  1. 将向量坐标看作拉伸或压缩向量的标量 第一个元素缩放i^\widehat{i}，第二个缩放j^\widehat{j}...etc. 压缩后基和即为所求向量

  2. 原点一定，对基的选择不同，导致得到的坐标系会不同 标准坐标系

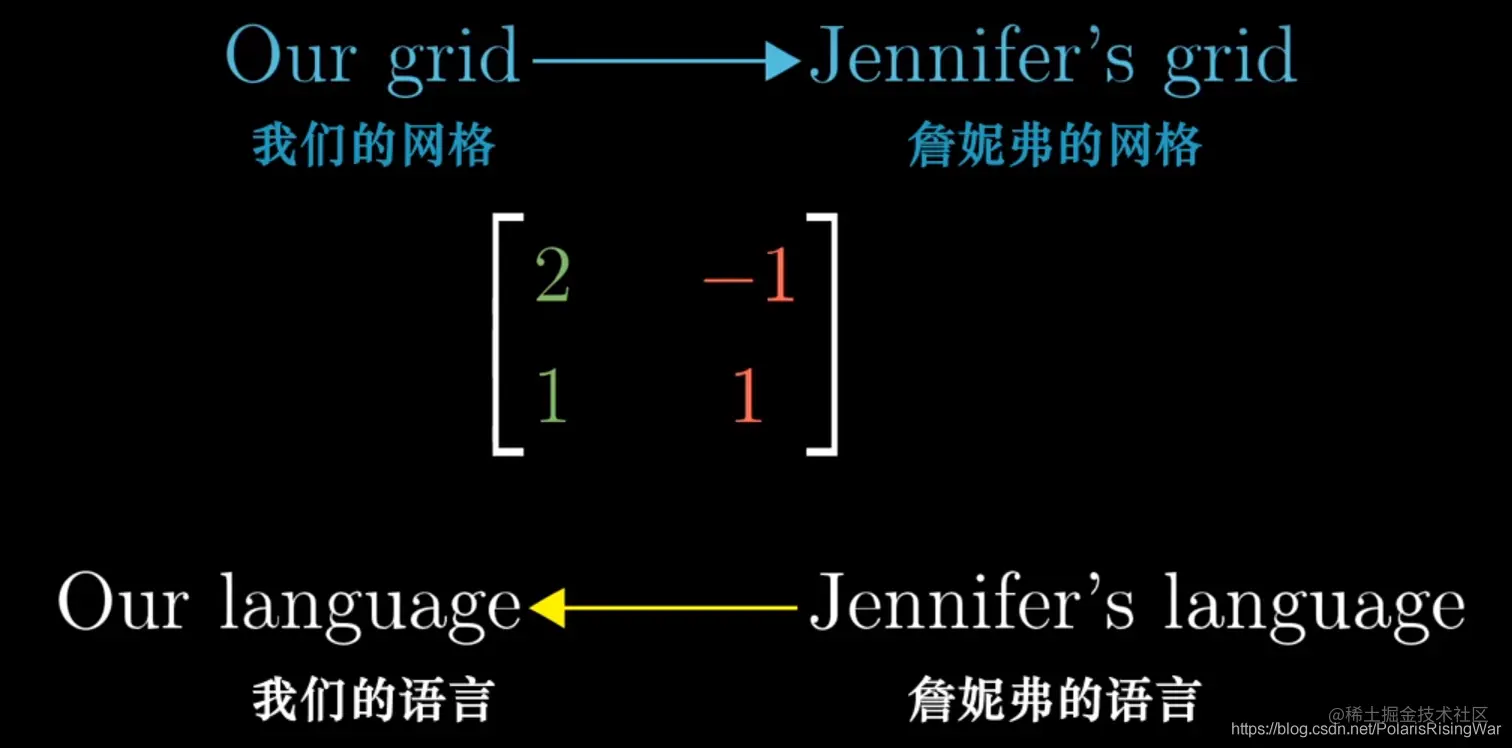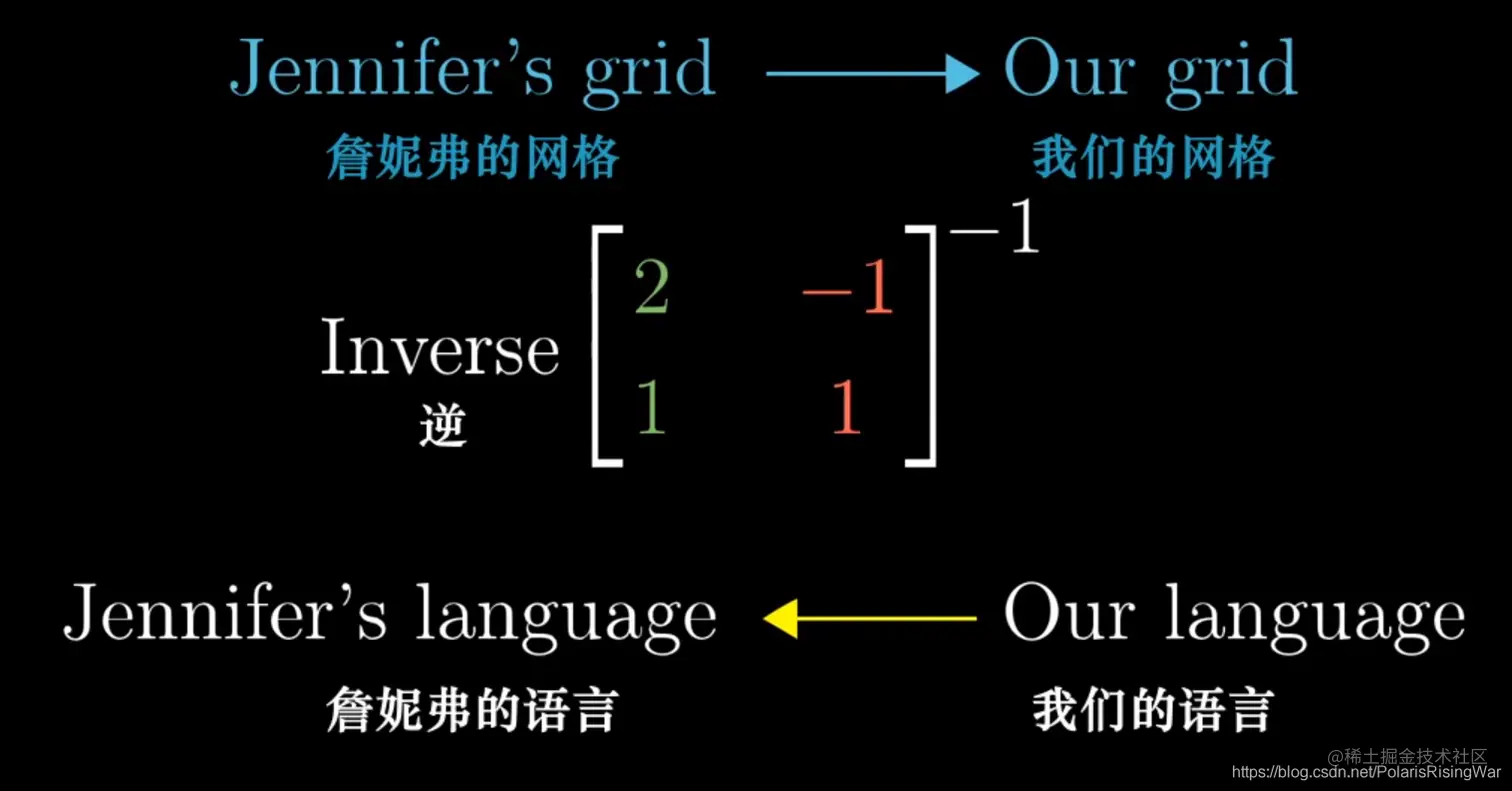
  3. 转换：矩阵（基）向量乘法在这里插入图片描述 逆在这里插入图片描述 在这里插入图片描述 在这里插入图片描述

  4. 基变换→线性变换→基变换的逆 A−1MAA^{-1}MA暗示着一种数学上的转移作用 这是一个跟M一样的变换，但是以另一种视角（基向量）来看的（在基变换后的坐标系上做变换，然后转到标准坐标系上）

10. 特征向量与特征值

  1. 在线性变换中，大部分向量离开了它生成的空间
  2. 线性变换的特征向量则仍留在它所张成的空间里 矩阵对它仅作拉伸或压缩（就像一个标量：特征值衡量比例的因子） 线性性质：特征向量张成空间内所有向量都会这样
  3. 旋转轴（特征值为1）（三维空间的特征向量） 我们过去对线性变换的描述过多依赖于特定的空间坐标系了（基坐标的变换），用特征向量和特征值其实能更好地理解线性变换
  4. 计算方式： Av→=λv→=(λI)v→A\overrightarrow{v}=\lambda\overrightarrow{v}=(\lambda I)\overrightarrow{v} (A−λI)v→=0→(A-\lambda I)\overrightarrow{v}=\overrightarrow{0} ① 如果v→=0\overrightarrow{v}=0的话上式永远成立。但是我们主要要找一个非零特征向量 情况就是：det(A−λI)=0⇐det(A-\lambda I)=0\Leftarrow这是一个空间压缩 这样算出特征值后就能代入①式求出特征向量
  5. 有的线性变换没有特征向量 有的线性变换的一个特征值对应多个特征向量（可以不在一条直线上）
  6. 特征基 基向量就是特征向量 对角矩阵：每列是特征向量，对角上的元素是特征值 （用对角矩阵多次左乘向量，会很好计算） 选择能张成全空间的特征向量，用特征向量作基（基变换）A A−1MAA^{-1}MA  M：原始的变换  特征基视角下的变换 线性变换得到的结果：是对角，且对角元为对应的特征值（它所处的坐标系里的基向量只做了缩放） 有的线性变换做不了这件事，它们的特征向量不够 用处：矩阵幂次计算

11. 抽象向量空间

  1. 有向量性质的东西
  2. 函数
    1. 函数相加是逐自变量相加，向量相加是逐元素相加
    2. 数乘
    3. 线性变换/线性算子：如导数/微分算子（可加性的严格定理见本系列笔记第3章）
    4. 举例来说，以全体多项式为一个空间，可以以1，xx，x2x^{2}，x3x^{3}...为基函数在这里插入图片描述
    5. 在这里插入图片描述
  3. 有很多数学事物都跟向量一样（只要对象集具有合理的数乘和相加概念） 类似向量的事物：向量空间——8条公理 在这里插入图片描述

12. 克莱姆法则，几何解释

  1. Ax→=v→A\overrightarrow{x}=\overrightarrow{v} 本章仅考虑非零行列式情况 二维：输入向量与基向量分别形成的平行四边形的面积（有向）就是其x/y的值 三维：输入向量某轴上的值，是该向量与另外两轴基向量形成的平行六面体体积
    所有面积伸缩的比例都等于给定的行列式（也就是说，变换后的面积是：det(A)×y（或x）det(A)\times y（或x）） 所以可以这么算y：y=Areadet⁡(A)y=\dfrac{\text{Area}}{\det \left( A\right) } 其中，det⁡(A)\det(A)是可算的，而AreaArea是用这个输入向量与基向量组成的新矩阵的行列式来算出来的 克莱姆法则
  2. 正交变换（旋转）：不改变点积的变换
  3. 更快的解法：高斯消元法
avatar
文章
阅读
粉丝