Stochastic Back Propagation （Reparametrization Trick）

本章主要介绍的是，神经网络用 $Y=f(X;\theta)$ 函数逼近器，那么我们将想想神经网络和概率图模型之间有什么关系呢？能不能用NN去逼近一个概率分布 $P(X)$ 呢？把他们两结合到一起就是随机后向传播，或者称之为重参数技巧。

正常情况下简单举例

假设 $P(Y)$ 是目标分布，其中 $P(Y)\sim \mathcal{N}(\mu,\sigma^2)$ 。我们之前是怎么采样的呢？是先从一个简单的高斯分布中进行采样 $Z\sim \mathcal{N}(0,1)$ ，然后令 $Y = \mu + \sigma Z$ ，就相当于一个二元一次变换。这样就可以得到采样方法：

\begin{equation} \left\{ \begin{array}{ll} z^{(i)} \sim \mathcal{N}(0,1) & \\ y^{(i)} = \mu + \sigma z^{(i)} & \\ \end{array} \right. \end{equation}

那么很自然的可以将此函数看成，{ $y=f(\mu, \sigma, z)$ }。这是一个关于 $z$ 的函数， $\mu, \sigma$ 假设是确定性变量，也就是当 $z$ 确定时，函数的值是确定的。那么，算法的目标就是找到一个函数映射 $z\mapsto y$ ，函数的参数为 $\{ \mu,\sigma \}$ 。

假设， $J(y)$ 是目标函数。那么梯度求导方法为：

\begin{equation} \frac{\nabla J(y)}{\nabla \theta} = \frac{\nabla J(y)}{\nabla y} \frac{\nabla y}{\nabla \theta} \end{equation}

条件概率密度函数}

假设目标分布为 $P(Y|X)=\mathcal{N}(X;\mu,\sigma^2)$ ，那么，在简单高斯分布 $Z \sim \mathcal{N}(0,1)$ 进行采样，可以得到，

\begin{equation} Y=\mu(X) + \sigma(X)Z \end{equation}

实际上可以将 $X$ 看成输入， $Z$ 看成是噪声， $Y$ 则是输出。神经网络的参数为 $\theta$ 。那么逻辑关系为：

\begin{equation} Y = \mu_\theta(X) + \sigma_\theta(X)Z \end{equation}

网络的模型如下所示：

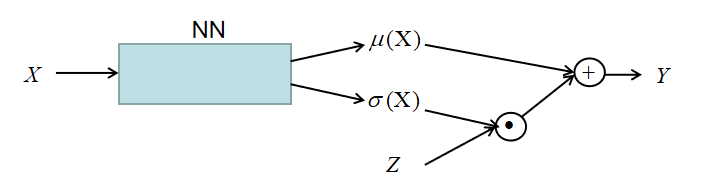
网络逻辑关系

其中， $\mu(X)=f(X;\theta),\sigma(X)=f(X;\theta)$ 。损失函数为：

\begin{equation} L_\theta(Y) = \sum_{i=1}^N \|y-y^{(i)}\|^2 \end{equation}

链式求导法则为：

\begin{equation} \frac{\nabla J_\theta(Y)}{\nabla \theta} = \frac{\nabla J_\theta(Y)}{\nabla Y}\frac{\nabla Y}{\nabla \mu}\frac{\nabla \mu}{\nabla \theta} + \frac{\nabla J_\theta(Y)}{\nabla Y}\frac{\nabla Y}{\nabla \sigma}\frac{\nabla \sigma}{\nabla \theta} \end{equation}

这样就可以做到用NN来近似概率密度函数，观测这个式子发现 $Y$ 必须要是连续可微的，不然怎么求 $\frac{\nabla Y}{\nabla \sigma}$ 。实际上这个模型可以被写为 $P(Y|X;\theta)$ ，将 $X,\theta$ 合并到一起就是 $w$ ，所以模型也可以被写为 $P(Y|w)$

小结

这小结从用神经网络来近似概率分布的角度分析两种概率分布模型，简单的高斯分布和条件高斯模型。并简要的介绍了其链式求导法则。

总结

本章节主要是对于概率生成模型进行了一个全面的介绍，起到一个承上启下的作用。回顾了之前写到的浅层概率生成模型，并引出了接下来要介绍的深度概率生成模型。并从任务（监督 vs 非监督），模型表示，模型推断，模型学习四个方面对概率生成模型做了分类。并从极大似然的角度重新对模型做了分类。并介绍了概率图模型和神经网络的区别，我觉得其中最重要的是，概率图模式是对样本数据建模，其图模型有具体的意义；而神经网络只是函数逼近器，只能被称为计算图。

参考B站视频【机器学习】【白板推导系列】

更多干货，第一时间更新在以下微信公众号：

您的一点点支持，是我后续更多的创造和贡献

转载到请包括本文地址更详细的转载事宜请参考文章如何转载/引用

本文由mdnice多平台发布

生成模型6-重参数技巧

Stochastic Back Propagation （Reparametrization Trick）

正常情况下简单举例

条件概率密度函数}

小结

总结