使用ADMM的Huber拟合

吴欣
453 阅读4分钟

Huber Fitting一般是指使用Huber函数来拟合数据模型的方法，这种方法的优势在于Huber函数的巧妙表述，它出色地结合了前面LAD和LS两种优化解法的最佳特征。为了受益于它的理论优势，必须对它进行求解，以获得可以在实践中使用的形式。为了更好地理解，建议对ADMM有一个扎实的了解。

目录

  1. 简介
  2. 机器学习的背景
  3. 使用ADMM解决Huber拟合问题
  4. 实施

简介

Huber损失函数是一个双片函数，定义如下

hub

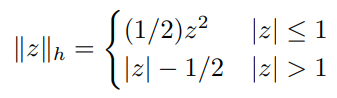
我们现在将研究Huber损失函数的激励机制。

考虑一下LAD（标记为绝对误差）、LS（标记为平方误差）和
Huber损失
的损失与预测误差的关系图
。

cmp-1

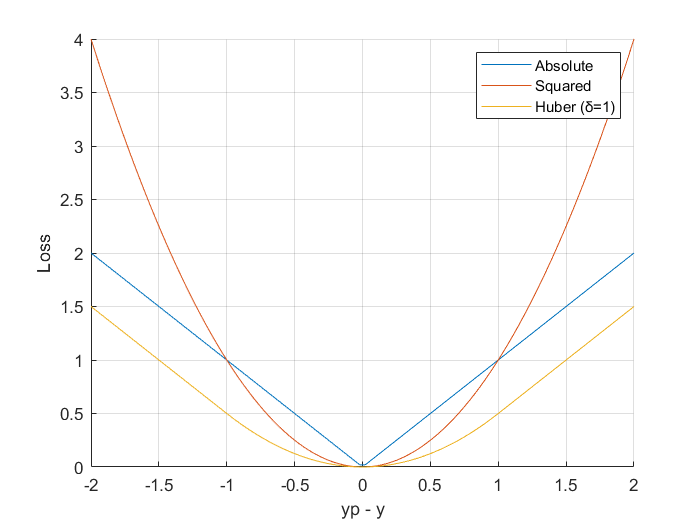
我们可以观察到。

  1. 在值[-δ, +δ]的范围内，LS误差小于LAD误差。
  2. 在（-∞，-δ）∪（+δ，+∞）的范围内，LAD误差小于LS误差

根据上述观察，我们可以制定Huber损失函数，明确使用在两个范围内表现更好的Errors。

机器学习的背景

在ML应用中经常使用的Huber损失函数的一般化形式是。

1-5

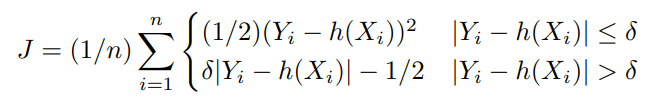
这里。

  • Y是观察值/实际值
  • h(Xi)是预测值

使用ADMM解决Huber拟合问题

因此，Huber拟合问题可以被定义为。

2-1

3-1

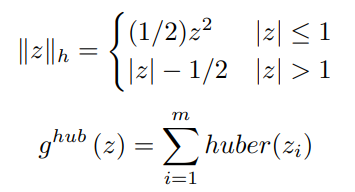
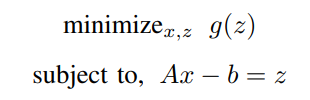
这里，x∈R^n，A是一个大小为mxn的矩阵，b是一个维度为mx1的向量。

ADMM解决方案。

相应的Augmented Lagrangian形式可以写为。

4-1

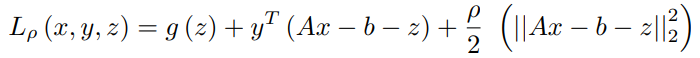
用u代替y/ρ，用λ代替1/ρ。

5-1

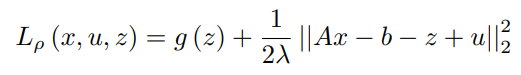
为了找到x的更新，关于x的拉格朗日的最小化是这样做的。

假设z^k和u^k是已知的。

6-1

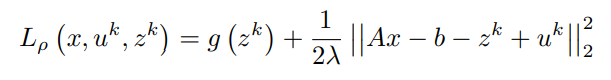
将关于x的一阶偏微分项等价为0（0矢量），简化后得到x^(k+1)

7-1

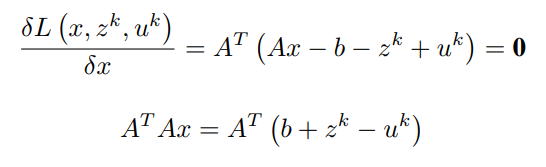
最后，x的更新由以下公式给出。

8-1

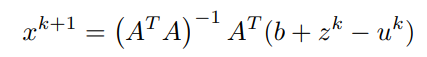
同样地，为了找到z的更新，对z的拉格朗日进行最小化，因为
x^(k+1)已被计算，u^k被假定为已知。

9-1

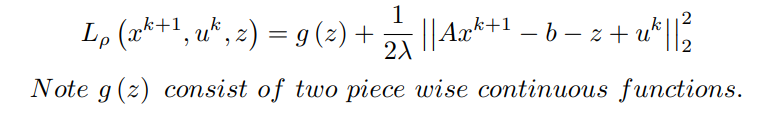
案例 - I :

10-1

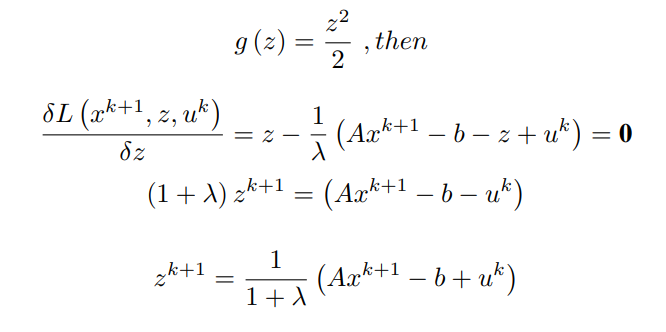
情况--II:

11-1

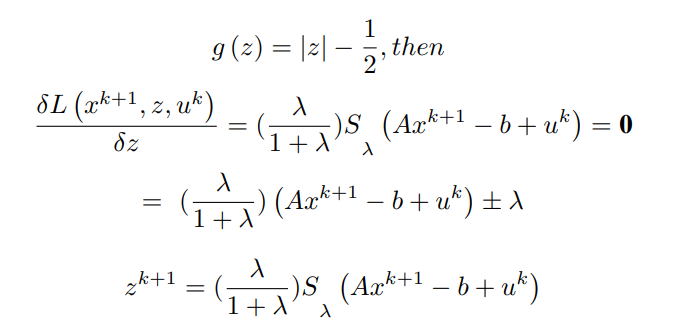
这里的Sλ代表±λ符号的缩减

我们可以反过来将最后的方程结合起来，得到。

12-1

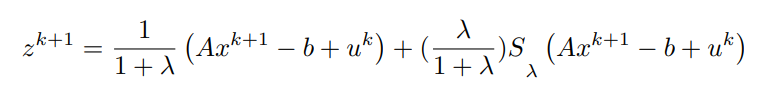
x^(k+1)和z^(k+1)都已经计算出来了，利用它们，y的更新可以写成：
原始拉格朗日乘数项是u.T
(Ax - b - z)

13-1

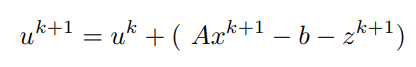
在本质上。

14-1

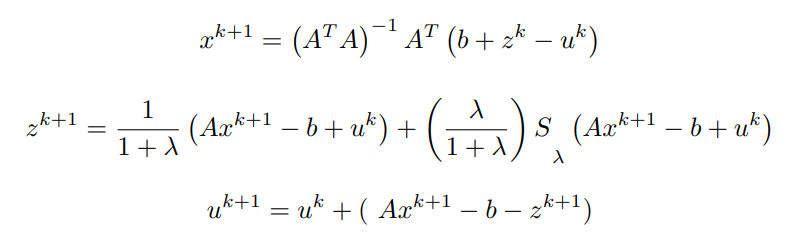
实施

在Matlab中对合成数据的更新步骤进行简单而直观的代码实现，可以按照基本步骤进行。

  1. 创建一个玩具数据集（可能是像下面这样的线性数据集），我们的目的是验证更新是否按计划进行。
  2. 决定一个目标变量（在下面的实现中，它将是变量x0），并向系统添加噪声，这是为了模仿一个更真实的观察。
  3. 随机初始化所需的变量/为零。
  4. 对更新方程进行编码，并在其中循环足够多的次数/直到收敛。
  5. 输出由更新得到的最终值，如果做得正确，我们应该观察到一个相对接近的curated值和由系统定义的更新得到的预测值。
randn('seed', 0);
rand('seed',0);

m = 5000;  % number of examples
n = 200;   % number of features

% synthesizing required conditions
x0 = sprandn(n,1,rho); 
A = randn(m,n);
A = A*spdiags(1./norms(A)',0,n,n); % normalize columns
b = A*x0 + sqrt(0.01)*randn(m,1);
b = b + 10*sprand(m,1,200/m);      % adding sparse, large noise
rho = 1;

MAX_ITER = 1000;
[m, n] = size(A);

% save a matrix-vector multiply
Atb = A'*b;
x = zeros(n,1);
z = zeros(m,1);
u = zeros(m,1);
P= inv(A'*A)

for k = 1:MAX_ITER
    % x-update
    x_new = P*(A'*(b+z-u));
    
    e  =  A*x_new;
    tmp = e - b + u;
    
    % z - update 
    z_new = rho/(1 + rho)*tmp + 1/(1 + rho)*shrinkage(tmp,1/rho);
    % u - update
    u_new = u + (e - z_new - b);
end 

h = {'x0' 'x'};
v = [x0, x_new];
R = [h;num2cell(v)]
oh = {'z' 'u'};
ov = [z_new, u_new];
oR = [oh;num2cell(ov)]

Matlab对辅助功能缩减的定义是。

function z = shrinkage(x, kappa)
    z = pos(1 - kappa./abs(x)).*x;
end

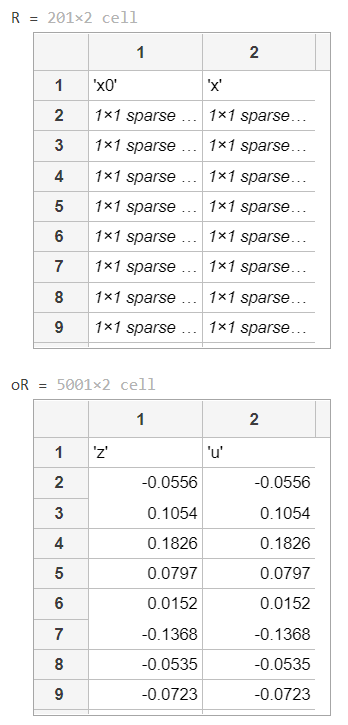
输出

得到以下输出。

这里：

  • x0代表我们期望通过更新在x中实现的综合数据
  • 而z和u是相应的更新支持性变量值

huber_out

L1-Norm与L2-Norm损失与误差图的附加代码

clc
clear all
close all

x = linspace(-2,2,100);

LAD = abs(x)

LS  = power(x,2)

delta = 1
set_1 = abs(x) <= delta;
set_2 = abs(x) > delta;

Huber = 0.5*set_1.*power(x,2) + set_2.*(abs(x) - 0.5)

hold on
grid on
xlim([-2,2]);
xticks(-2:0.5:2);
ylim([0,4]);
yticks(0:0.5:4);

% Error = actual - predicted
xlabel("yp - y")
ylabel("Loss")
plot(x, LAD)
plot(x, LS)
plot(x, Huber)
legend('Absolute', 'Squared', 'Huber (δ=1)')
avatar
文章
阅读
粉丝