迭代式顺序内遍历

在这篇文章中，我们探讨了迭代顺序内遍历的概念，以及详细的一步一步的例子和完整的实现。

目录

1. 定义
2. 算法
3. 时间复杂度
4. 实现方式

1.定义

二叉树是一种数据结构，每个节点只包含对其他节点的两个引用。通常它们被称为左和右，但你也可以用其他方式命名，例如：向上和向下或阴和阳，等等。

有不同的方法来遍历一棵树。其中一种是按顺序的，意思是一个节点被访问：
* 首先是它的左边节点
* 其次是它的值
* 第三是它的右边节点

我们可以递归地或迭代地进行，
为了比较，我们将采用这两种方式。

2.算法

二叉树无序遍历的迭代伪码算法如下1:

procedure visitNode(node)
    stack ← empty stack
    while not stack is not empty or node is not null
        if node is not null
            stack.push(node)
            node ← node.left
        else
            node ← stack.pop()
            visit(node)
            node ← node.right

注意到堆栈的使用，这意味着一个后进先出的数据结构，它保存着被访问节点的值。

3.时间复杂度

对于图来说，深度优先遍历的复杂度是O(n+m)，其中n是节点的数量，m是边的数量。

由于二叉树也是一个图，所以同样适用于此。每个深度优先遍历的复杂性都是O(n+m)。

由于在二叉树的情况下，可以从一个节点出发的边的数量被限制在2条，所以二叉树中总的边的最大数量是n-1，其中n是节点的总数。

那么复杂度就变成了O(n+n-1)，也就是O(n)。2

4.一种实现方式

接下来的程序将使用递归和迭代函数来遍历二叉树，并使用堆栈库来保存节点的值。如果我们不想使用该库，那么我们就需要自己实现一个。

#include <iostream>
#include <stack>

using namespace std;

struct Node
{
    int val;
    Node *left = NULL;
    Node *right = NULL;
};

void visitNodeRecursive(Node *n)
{
    if (n != NULL)
        {
            visitNodeRecursive(n->left);
            cout << n->val<<" ";
            visitNodeRecursive(n->right);
        }
}

void visitNodeIterative(Node *n)
{
    stack<Node *> s;
    
    while ( ! s.empty() || n != NULL)
        {
            if (n != NULL)
                {
                    s.push(n);
                    n = n->left;
                }
            else
                {   n = s.top();
                    cout<< n->val<<" ";
                    s.pop();
                    n = n->right;
                }
        }
}

int main()
{
    Node n1,n2,n3,n4,n5,n6,n7;
    n1.val = 1;
    n2.val = 2;
    n3.val = 3;
    n4.val = 4;
    n5.val = 5;
    n6.val = 6;
    n7.val = 7;
    
    n1.left = &n2;
    n1.right = &n3;
    
    n2.left = &n4;
    n2.right = &n6;
    
    n3.left = &n5;
    //n3.right = NULL;
    
    //n4.left = NULL;
    n4.right = &n7;
    
    
    visitNodeRecursive(&n1);
    cout<<endl;
    visitNodeIterative(&n1);
    
    return 0;
}

输出：

4 7 2 6 1 5 3
4 7 2 6 1 5 3

在这个实现中，我们声明了7个Node类型的对象。
一个Node是一个结构类型。你也可以使用类类型的实现。

上述二叉树的结构会是这样的。

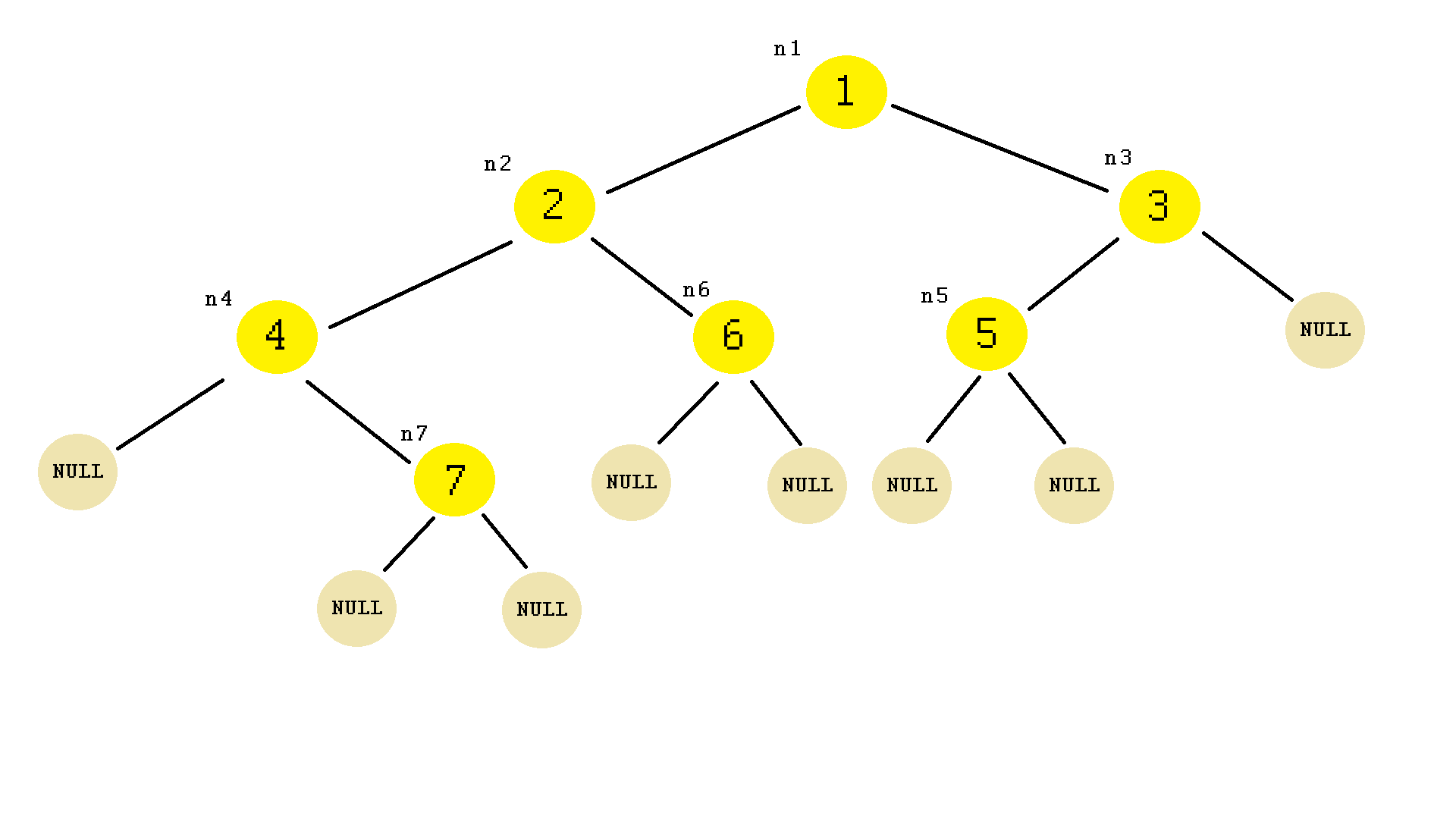
注意左边和右边的Node指针的初始化为NULL，这是实现二叉树结构的一个关键点。试着去掉这一点，在运行程序时初始化指针，你会得到另一个结果。

使用堆栈进行迭代遍历的逐案例子。