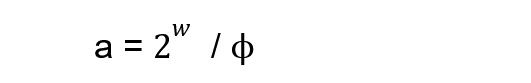讨论一种被忽视的哈希函数

目录

1. 简介
2. Fibonacci Hashing
3. 代码实现
4. 时间复杂度
5. 比较
6. 应用

简介

本文将讨论一种被忽视的哈希函数，即斐波那契哈希。它是另一种形式的乘法散列函数，与黄金比例有关。这可以作为其他散列函数的替代品；它比顺序和二进制搜索更快。我们将讨论它如何工作和实现。

斐波那契散列

首先简单回顾一下散列，它是常见的搜索算法之一。它使用散列表，散列表是用于将键映射到值的数据结构。使用散列函数，将计算出对每个输入都是唯一的散列值。然后，每个哈希值被均匀地分布在一个哈希表中。有不同的哈希函数，如除法、中平方、折叠和乘法等方法。

斐波那契散列只是乘法散列的另一种形式。在一个乘法散列函数中，它使用的是公式。

其中：
a = 实数
w = 字位大小
k = 整数哈希代码
m = 表大小
m = 2r

在斐波那契散列中，不是使用一个随机的整数作为a，而是使用黄金分割率来分割2w。

其中Φ=1.618

例如，我们有一个有512个槽的哈希表和一个有32位大小的字的哈希值。我们的a值将是232/ Φ = 2654442313。接下来的过程将在下图中进一步讨论

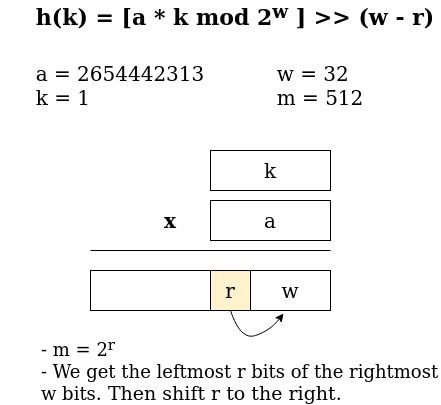
让我们试着用C++实现这个过程，看看结果如何。

代码实现

   hash(int x) {
   // the value for a using golden ratio
   const std::uint32_t hash = 2654442313;
   const std::uint32_t y = x;
   // look at the top 3 bits of the hash value
   return (y * hash) >> (29);
   }

   int main() {

       for(int x=0; x<17; x++)  
       cout<<hash(x)<<endl;
       return 0;
   }

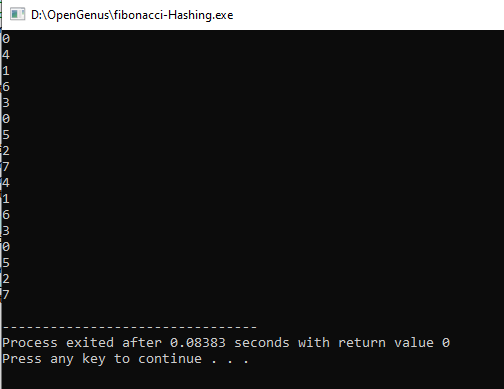
输出

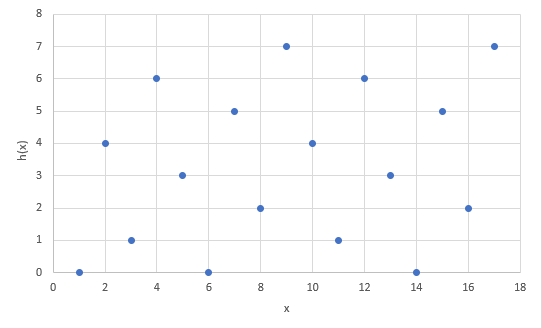
输出显示了每个散列值的最高位，因此我们可以看到斐波那契散列的工作模式。根据结果，我们可以看到每个值都是均匀分布的。如果我们将其映射到一个图中，我们就可以看到这个模式。

在实现多重复散列时使用黄金比例有助于使连续的密钥随机但均匀地分布。

斐波那契散列法实现了一个更快的散列方法，它产生了一个混合的输入模式。然而，它可能导致高概率的碰撞。一项研究在指纹系统的快速检索算法中实现了斐波那契散列，请看这里。斐波那契散列法是一种在小空间内存储大数值的好技术，因为它在散列表中占了大部分的空间。

比较

这种方法也可以很快，但只有在m是素数且不太接近2的幂数时才最适合，如果m和k之间有公因数且表的大小是2的幂数，它就会有问题，因为它只占据/使用一半的表，所以效率很低。

与使用黄金比例的乘法散列（h(k) = [ a*k mod 2^w] >> (w-r)）相比，它在任何表大小下都能很好地工作。使用黄金比例，我们已经得到了a的理想值，因此我们已经得到了一个理想值，可以在哈希表中均匀地分配连续的键。

复杂度

空间复杂性。 **Θ(2m)**
其中m是表/列表的大小

时间复杂度。

取决于碰撞的概率，如果较小，那么它的平均值为 **Θ(1)**
我们还应该考虑表的大小。如果表大，那么它的碰撞就少，如果小，那么碰撞的概率就大。

应用

一项研究在指纹系统的快速检索算法中实现了斐波那契散列，请看这里。斐波那契散列法是一种在小空间内存储大数值的好技术，因为它在散列表中占了大部分的空间。

斐波那契散列法也被用于一项生物信息学研究中。它被用于一个蛋白质家族的识别，其中每个氨基酸代码被分配给基于整数表示的斐波那契数字。在这里阅读它。