Solidity 是一种静态类型语言,这意味着每个变量(状态变量和局部变量)都需要在编译时指定变量的类型。
合约中到处充斥着变量,包括状态变量,函数中的变量,结构体的变量等等
“undefined”或“null”值的概念在Solidity中不存在,但是新声明的变量总是有一个 默认值 ,具体的默认值跟类型相关。
关于类型这块,文档写的很清楚了,learnblockchain.cn/docs/solidi…
值类型
当这些变量被用作函数参数或者用在赋值语句中时,总会进行值拷贝。
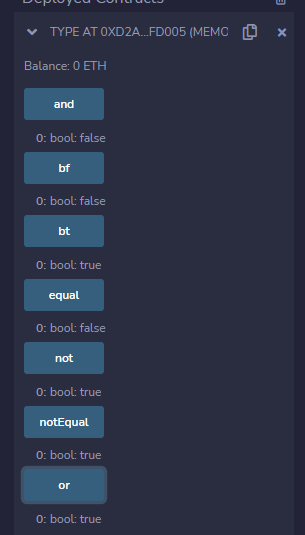
布尔类型
// SPDX-License-Identifier: GPL-3.0
pragma solidity 0.8.17;
contract BoolType {
// 默认值false
bool public bf;
// 可在定义时赋值
bool public bt = true;
// 逻辑非
function not() public view returns (bool) {
return !bf;
}
// 逻辑与
function and() public view returns (bool) {
return bf&&bt;
}
// 逻辑或
function or() public view returns (bool) {
return bf||bt;
}
// 等于
function equal() public view returns (bool) {
return bf==bt;
}
// 不等于
function notEqual() public view returns (bool) {
return bf!=bt;
}
}
运算符 || 和 && 都遵循同样的短路规则。就是说在表达式 f(x) || g(y) 中, 如果 f(x) 的值为 true ,那么 g(y) 就不会被执行,即使会出现一些副作用。
整型
int / uint :分别表示有符号和无符号的不同位数的整型变量。 支持关键字 uint8 到 uint256 (无符号,从 8 位到 256 位)以及 int8 到 int256,以 8 位为步长递增。 uint 和 int 分别是 uint256 和 int256 的别名。
int a; // 默认0
uint b=2; // 定义时赋值
整形支持
比较
<= , < , == , != , >= , > (返回布尔值),比较简单,数字之间的大小比较
位运算
二进制
在了解位运算之前,我们需要先了解二进制的表现形式
让我们先观察一个数字,2871,
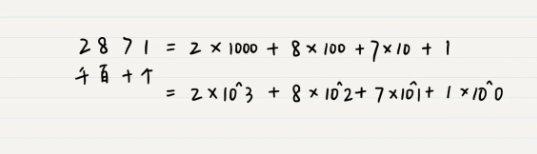
其中 ^ 表示幂或次方运算。十进制的数位(千位、百位、十位等)全部都是 10^n 的形式。需要特别注意的是,任何非 0 数字的 0 次方均为 1。在这个新的表示式里,10 被称为十进制计数法的基数,也是十进制中“十”的由来。
我们再试着用类似的思路来理解二进制的定义。
十进制计数是使用 10 作为基数,那么二进制就是使用 2 作为基数,类比过来,二进制的数位就是 2^n 的形式。
我以二进制数字 110101 为例
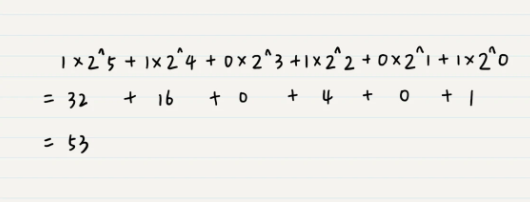
按照这个思路,我们还可以推导出八进制(以 8 为基数)、十六进制(以 16 为基数)等等计数法
我们可以通过除n取余法来转换10进制为n进制,以789为例,想要转换成2进制,那么就是
789/2=394 余1 第10位
394/2=197 余0 第9位
197/2=98 余1 第8位
98/2=49 余0 第7位
49/2=24 余1 第6位
24/2=12 余0 第5位
12/2=6 余0 第4位
6/2=3 余0 第3位
3/2=1 余1 第2位
1/2=0 余1 第1位
除到商为0停止,然后,从后往前,把余数整合起来,就是对应的2进制了。该方法也叫除2取余法,所以
789(10)=1100010101(2)
在js中可以直接利用Number('789').toString(2)来实现10进制转换为n进制,当然js也可以通过parseInt('1100010101',2)把2进制转换成10进制
在Solidity中整形有 有符号整形和无符号整形
有符号整形的最高位为符号位,用他来表示正数还是负数,当符号位为0时,表示该数值为正数,当符号位为1时,表示该数值为负数
例如一个 8 位的有符号位二进制数 10100010,最高位是 1,这就表示它是一个负数。由于没有表示负数的符号位,所有无符号位的二进制都代表正数。
如果是无符号数,那么最高位就不是符号位,而是二进制数字的一部分
溢出
在数学的理论中,数字可以有无穷大,也有无穷小。可是,现实中的计算机系统,总有一个物理上的极限(比如说晶体管的大小和数量),因此不可能表示无穷大或者无穷小的数字。对计算机而言,无论是何种数据类型,都有一个上限和下限。
在solidity中,int 是 256位,它的最大值也就是上限是 2^255^-1(最高位是符号位,所以是 2 的 255 次方而不是 256 次方),最小值也就是下限是 -2^255。
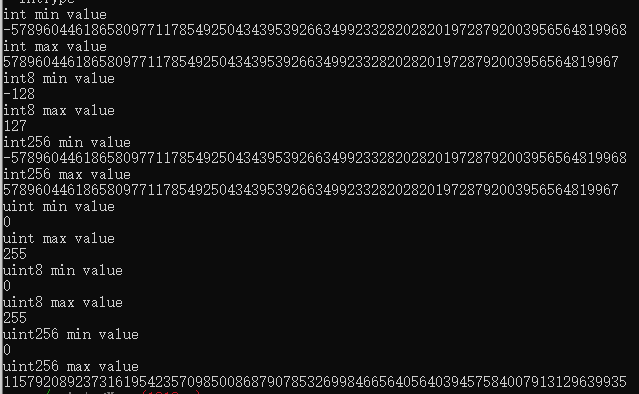
在Solidity中,对于整形 X,可以使用 type(X).min 和 type(X).max 去获取这个类型的最小值与最大值。
对于int,范围在 -2^255^ 到 2^255^-1之间
对于uint,范围在 0到 2^256^-1之间
// SPDX-License-Identifier: GPL-3.0
pragma solidity 0.8.17;
import "hardhat/console.sol";
contract IntType {
function minAndMax() public view {
console.log("int min value");
console.logInt(type(int).min);
console.log("int max value");
console.logInt(type(int).max);
console.log("int8 min value");
console.logInt(type(int8).min);
console.log("int8 max value");
console.logInt(type(int8).max);
console.log("int256 min value");
console.logInt(type(int256).min);
console.log("int256 max value");
console.logInt(type(int256).max);
console.log("uint min value");
console.log(type(uint).min);
console.log("uint max value");
console.log(type(uint8).max);
console.log("uint8 min value");
console.log(type(uint8).min);
console.log("uint8 max value");
console.log(type(uint8).max);
console.log("uint256 min value");
console.log(type(uint256).min);
console.log("uint256 max value");
console.log(type(uint256).max);
}
}
一旦某个数字超过了这些限定,就会发生溢出。如果超出上限,就叫上溢出(overflow)。如果超出了下限,就叫下溢出(underflow)。
溢出之后会发生什么呢
n 位数字的最大的正值,其符号位为 0,剩下的 n-1 位都为 1,再增大一个就变为了符号位为 1,剩下的 n-1 位都为 0。而符号位是 1,后面 n-1 位全是 0,我们已经说过这表示 -2^(n-1)。为能表示的最大负数
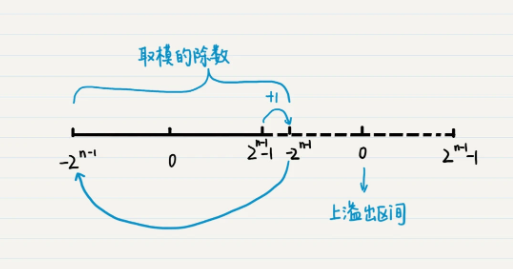
那么就是说,上溢出之后,又从下限开始,最大的数值加 1,就变成了最小的数值,周而复始,就像取模一样,
而用于取模的除数就是数据类型的上限减去下限的值,再加上 1,也就是
(2^(n-1)-1)-(-2^(n-1))+1=2x2^(n-1)-1+1=2^n-1+1。
原码、反码及补码
原码就是我们看到的二进制的原始表示。对于有符号的二进制来说,原码的最高位是符号位,而其余的位用来表示该数字绝对值的二进制。所以 +2 的原码是 000…010,-2 的的原码是 100.…010。
那么我们是不是可以直接使用负数的原码来进行减法计算呢?答案是否定的。我还是以 3+(-2) 为例。
我们用int,即256位来进行运算
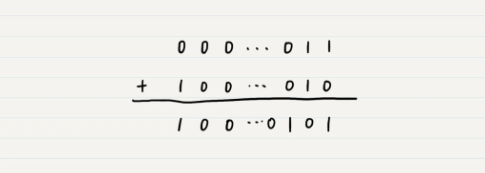
相加后的结果是二进制 100…0101,它的最高位是 1,表示负数,而最低的 3 位是 101,表示 5,所以结果就是 -5 的原码了,而 3+(-2) 应该等于 1,两者不符。
负数的原码不适用于减法操作,这个问题的解答还要依赖计算机的溢出机制。上面有讲到,溢出以及取模的特征,我们可以充分利用这一点,对计算机的减法进行变换,假设有 i-j,其中 j 为正数。如果 i-j 加上取模的除数,那么会形成溢出,并正好能够获得我们想要的 i-j 的运算结果。
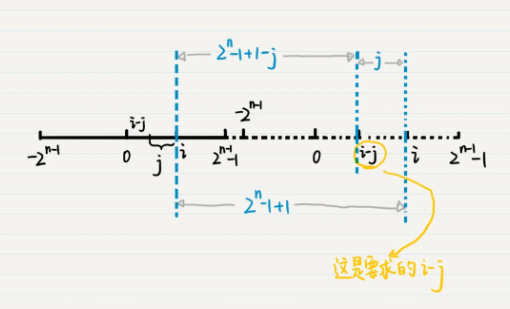
我们把这个过程用表达式写出来就是
i-j=(i-j)+(2^n-1+1)=i+(2^n-1-j+1)。
其中 2^n-1 的二进制码在不考虑符号位的情况下是 n-1 位的 1,那么 2^n-1-2 的结果就是下面这样的:
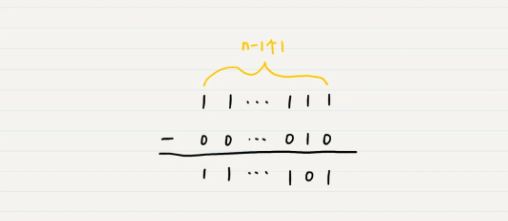
从结果可以观察出来,所谓 2^n-1-j 相当于对正数 j 的二进制原码,除了符号位之外按位取反(0 变 1,1 变 0)。由于负数 -j 和正数 j 的原码,除了符号位之外都是相同的,所以,2^n-1-j 也相当于对负数 -j 的二进制原码,除了符号位之外按位取反。我们把 2^n-1-j 所对应的编码称为负数 -j 的反码。所以,-2 的反码就是 1111…1101。
有了反码的定义,那么就可以得出 i-j=i+(2^n-1-j+1)=i 的原码 +(-j 的反码)+1。
如果我们把 -j 的反码加上 1 定义为 -j 的补码,就可以得到 i-j=i 的原码 +(-j 的补码)。
由于正数的加法无需负数的加法这样的变换,因此正数的原码、反码和补码三者都是一样的。最终,我们可以得到 i-j=i 的补码 +(-j 的补码)。
换句话说,计算机可以通过补码,正确地运算二进制减法。我们再来用 3+(-2) 来验证一下。正数 3 的补码仍然是 0000…0011,-2 的补码是 1111…1110,两者相加,最后得到了正确的结果 1 的二进制。
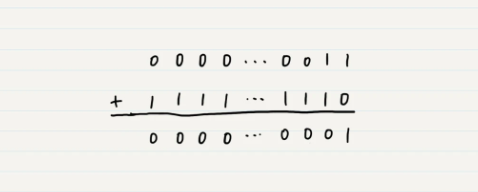
我们来看一下一个二进制负数的补码 10100010,
如果想知道他对应的十进制,按照 原码按位取反后+1得反码的规则,求的对应原码应该是 11011110,即-94,其实我们也可以对补码求补码,即取反后+1,也会是原码,两种方式本质是一样的
位运算
& (与), |(或) , ^ (异或), ~ (位取反),位运算在数字的二进制补码表示上执行。
function calcBit() public view{
int i = 0;
uint ui = 0;
console.logInt(~i);
console.log(~i==-1);
console.log(~ui);
console.log(~ui==type(uint).max);
}
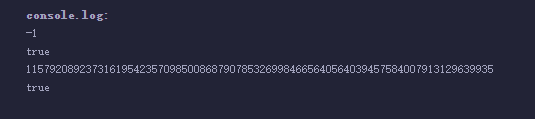
~int256(0)== int256(-1),因为0000....00000按位取反是11111.....1111,其补码+1是10000....0001,所以是-1
移位
有左移和右移,注意右操作数必须是无符号类型,移位的结果类型跟左操作数一致,同时会截断结果,不会执行溢出检查,结果会被截断
移位可以想象成乘 n 个2或者除以n个2,n为移位的个数,
举个例子,uint8 a = 3,实际为 00000011,我们左移移位,即,a<<1,那么就会变成00000110,是6,6刚好是3的2倍,所以,二进制左移一位,其实就是将数字翻倍。那左移两位,就是翻倍再翻倍。
右移一位,就是去除末尾的那一位, a>>1,那么就会变成00000011,是3,3>>1,就是00000001,是1,1。所以二进制右移一位,就是将数字除以 2 并求整数商的操作。
当然以上是在不考虑溢出的情况
uint8 01111111 左移一位,是11111110,还没溢出,左移两位,111111100,溢出,截掉超过的位,变成11111100,是 252,
function moveBit() public view{
uint8 ui8 = 127;
int8 i8 = -127;
console.log("left move 127,move 1",ui8<<1);
console.log("left move 127,move 2",ui8<<2);
console.log("left move 127,move 3",ui8<<3);
console.log("right move 127,move 1",ui8>>1);
console.log("right move 127,move 2",ui8>>2);
console.log("right move 127,move 6",ui8>>6);
console.log("right move 127,move 7",ui8>>7);
console.log("right move 127,move 8",ui8>>8);
console.log("left move -1,move 1");
console.logInt(i8<<1);
console.log("left move -1,move 2");
console.logInt(i8<<2);
console.log("left move -1,move 7");
console.logInt(i8<<7);
console.log("left move -1,move 8");
console.logInt(i8<<8);
}
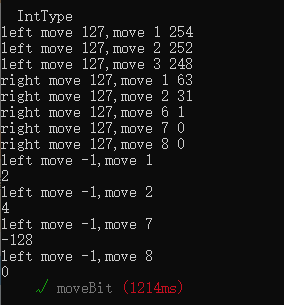
算数运算
加法,减法和乘法和通常理解的语义一样,不过有两种模式来应对溢出(上溢及下溢)
默认情况下,算术运算都会进行溢出检查,但是也可以禁用检查,可以通过 unchecked block 来禁用检查,此时会返回截断的结果
function calcOver() public view{
uint8 a = 2;
uint8 b=3;
unchecked { uint8 c = a-b;console.log('unchecked value:',c); }
uint8 d = a-b;
console.log(d);
}
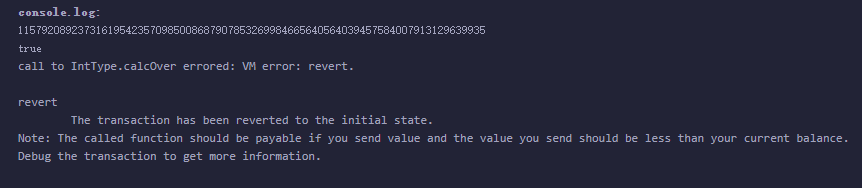
可以看到,如果使用uncheck,那么会截断,2-3=-1,-1去掉符号为2^256-1
除法:
在Solidity中,分数会取零。 这意味着 int256(-5) / int256(2) == int256(-2) 。
除以0 会发生 Panic 错误 , 而且这个检查,不可以通过 unchecked { ... } 禁用掉。
模
模运算 a%n 是在操作数 a 的除以 n 之后产生余数 r ,其中 q = int(a / n) 和 r = a - (n * q) 。 这意味着模运算结果与左操作数相同的符号相同(或零)。 对于 负数的a : a % n == -(-a % n), 几个例子:
int256(5) % int256(2) == int256(1)int256(5) % int256(-2) == int256(1)int256(-5) % int256(2) == int256(-1)int256(-5) % int256(-2) == int256(-1)
对0取模会发生错误 Panic 错误,该检查不能通过unchecked { … } 。
幂
幂运算仅适用于无符号类型。 结果的类型总是等于基数的类型. 请注意类型足够大以能够容纳幂运算的结果,要么发生潜在的assert异常或者使用截断模式。
uint(3)**uint(2)==uint(9)
注意 0**0 在EVM中定义为 1
定长浮点型
fixed / ufixed:表示各种大小的有符号和无符号的定长浮点型。 在关键字 ufixedMxN 和 fixedMxN 中,M 表示该类型占用的位数,N 表示可用的小数位数。 M 必须能整除 8,即 8 到 256 位。 N 则可以是从 0 到 80 之间的任意数。 ufixed 和 fixed 分别是 ufixed128x19 和 fixed128x19 的别名。
实际很少用,而且Solidity 还没有完全支持定长浮点型。建议尽量少用