具体

文章:[Denoising Diffusion Probabilistic Models]([2006.11239] Denoising Diffusion Probabilistic Models (arxiv.org))

可借鉴的学习视频：视频

代码：暂时未实现

条件概率公式和高斯分布的KL散度

条件概率的一般形式

基于马尔科夫链关系A->B->C ，那么有

高斯分布的KL散度公式

对于两个单一变量的高斯分布p,q 而言，它们的KL散度

对于两个正态分布$X-N(\mu_1,\sigma_1)$和$Y-N(\mu_2,\sigma_2)$的叠加后的分布aX+bY的均值为$a\mu_1+b\mu_2$,方差为$a^2\sigma_1^2+b^2+\sigma_2^2$。

因而对于

可以转换成

参数重整化

若希望从高斯分布$N(\mu,\sigma^2)$ 中采样，可以先从标准分布$N(0,1)$ 中采样出$z$ ，再得到$\sigma*z +\mu$ 。这也做的好处是将随机性转移到了$z$ 这个常量上，而$\sigma,\mu$ 则当作仿射变换网络的一部分。(为了可以梯度传播)

马克尔夫链

马尔可夫链（Markov Chain），描述了一种状态序列，其每个状态值取决于前面有限个状态。

马尔可夫链是满足下面两个假设的一种随机过程：

1、t+1时刻系统状态的概率分布只与t时刻的状态有关，与t时刻以前的状态无关；

2、从t时刻到t+1时刻的状态转移与t的值无关。一个马尔可夫链模型可表示为=(S,P,Q)，其中各元的含义如下：

1)S是系统所有可能的状态所组成的非空的状态集，有时也称之为系统的状态空间，它可以是有限的、可列的集合或任意非空集。本文中假定S是可数集（即有限或可列）。用小写字母i,j（或Si,Sj)等来表示状态。

2)P是系统的状态转移概率矩阵，其中Pij表示系统在时刻t处于状态i,在下一时刻t+l处于状态j的概率,N是系统所有可能的状态的个数。对于任意i∈s,有。

3)Q是系统的初始概率分布,qi是系统在初始时刻处于状态i的概率，满足。

Diffusion model

原理图示：

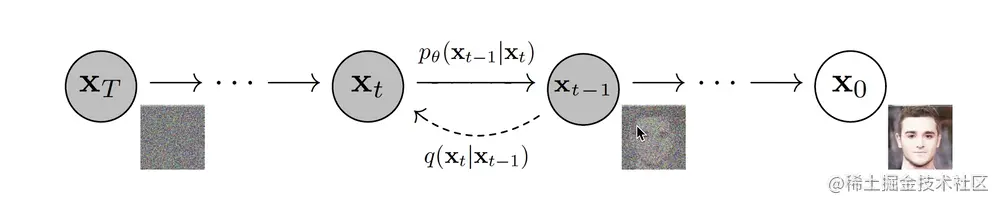
扩散步骤：

扩散过程本质上是逐渐对初始数据加入高斯噪声的步骤

它允许以封闭形式在任意时间步长t采样x_t，同时我们使用$\alpha_t=1-\beta_t,\bar{\alpha_t}=\Pi_{s=1}^{t}\alpha_s$

整体的实验过程当作我们对于$\beta_t$的变化是限制成线性增量的，即为$\beta_y\in(10^{-4},0.02)$之间

那儿我们就可以有下列的式子

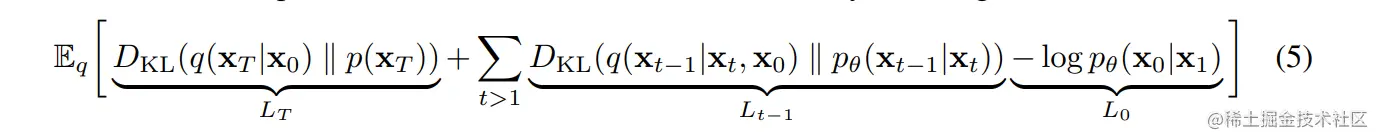
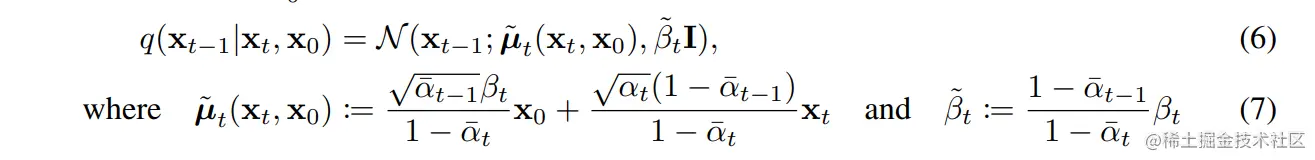
逆扩散步骤：

逆过程是从高斯噪声中恢复原始数据，我们可以假设它也是一个高斯分布，但是无法逐步地拟合分布，所以需要构建一个参数分布来去做估计。逆扩散过程仍然是一个马克尔夫链过程。

后验的扩散条件概率$q(x_{t-1}|x_t,x_0)$分布是可以用公式表达的

这也就是说，给定$x_t,x_0$,我们是可以计算出$x_{t-1}$

注意：高斯分布的概率密度函数$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp^{\frac{-(x-\mu)^2}{2\sigma^2}}$

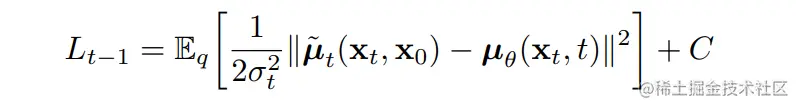
对于该式子，我们进行数据的替换，同时结合正向扩散的过程可以得到下列的式子

$x_t(x_0,\epsilon ) = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1-\bar{\alpha_t}}\epsilon \quad for\quad \epsilon ∼ N (0, I)$

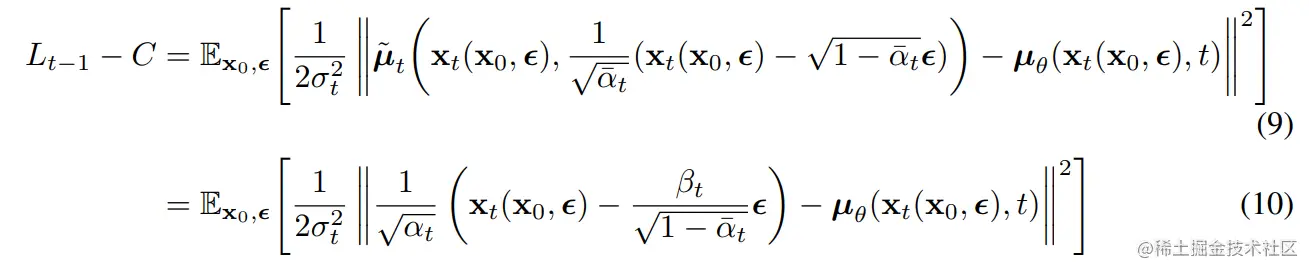
整体的思路