开启掘金成长之旅!这是我参与「掘金日新计划 · 12 月更文挑战」的第7天,点击查看活动详情
线性代数简明教程
线性代数
标量
简单操作
- c=a+b
- c=a×b
- c=sinα
长度
- ∣a∣={a−aifa>0otherwise
- ∣a+b∣≤∣a∣+∣b∣
- ∣a×b∣=∣a∣×∣b∣
向量
向量就是一行值(或者一列值),称作行向量、列向量
简单操作
- 定义:a,b都是向量、alpha是标量
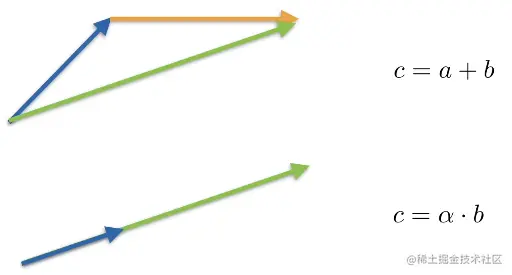
- c=a+b where ci=ai+bi
- c=α×b where ci=α×bi
- c=sina where ci=sinai
长度
-
∥∥a∥∥2=[∑i=1mai2]21
-
∥∥a∥∥≥0 for all a
-
∥∥a+b∥∥≤∥∥a∥∥+∥∥b∥∥
-
∥∥a×b∥∥=∥∥a∥∥×∥∥b∥∥
向量直观上的理解
点乘
- a⊤b=∑iaibi
- a⊤b=∑iaibi=0
正交
矩阵
简单操作
- C=A+B where Ci,j=Ai,j+Bi,j
- C=α×B where Ci,j=αBi,j
- C=sinA where Ci,j=sinAi,j
矩阵乘以向量
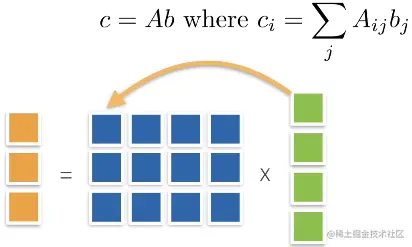 矩阵的每一行和列向量做内积(乘法)
矩阵的每一行和列向量做内积(乘法)
矩阵的乘法是在扭曲空间
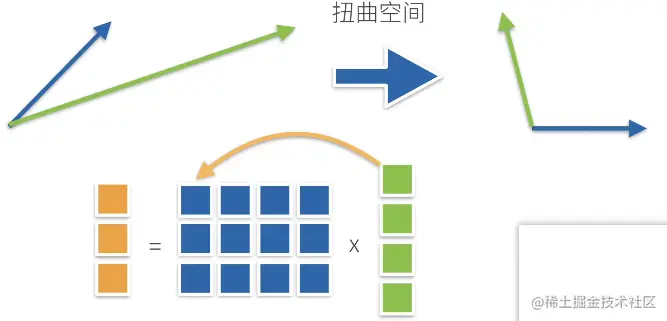
一个向量通过一个矩阵乘法变成了另外一个向量
矩阵乘法
- C=A×B where Ci,k=∑jAi,jBj,k
范数
对称和反对称
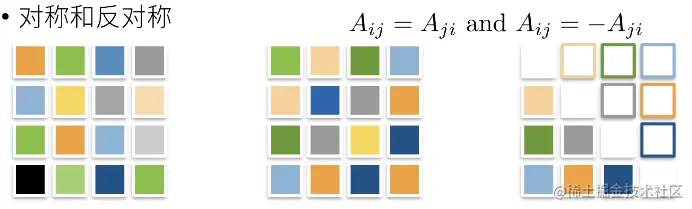
正交矩阵
置换矩阵
特征向量
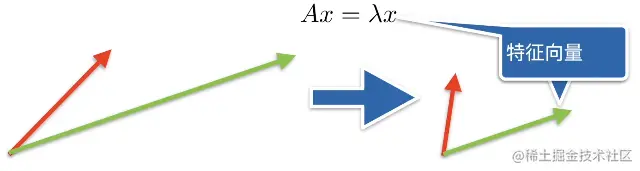
-
不被矩阵改变方向的向量
-
对称矩阵总是可以找到特征向量
-
但不是每个矩阵都有特征向量
pytorch
基础+-*/
向量就是标量组成的列表
a = torch.arange(4)
索引访问
a[0]
长度
len(a)
矩阵
创建一个5行4列的矩阵
A=torch.arange(20).reshape(5,4)
矩阵的转置(沿着对称轴翻转 \ )

A.T
对称矩阵的转置等于自身
向量是标量的推广,矩阵是向量的推广,可以基于此原理,构建具有更多轴的数据结构(任何维度)
创建一个三维矩阵
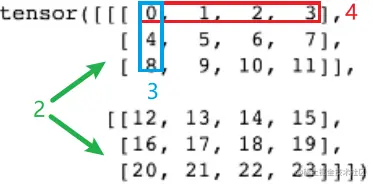
X=torch.arange(24).reshape(2,3,4)
注意2,3,4代表的是什么(从外到内)
哈达玛积(矩阵按元素乘)不常用
A*B
矩阵元素和(标量)
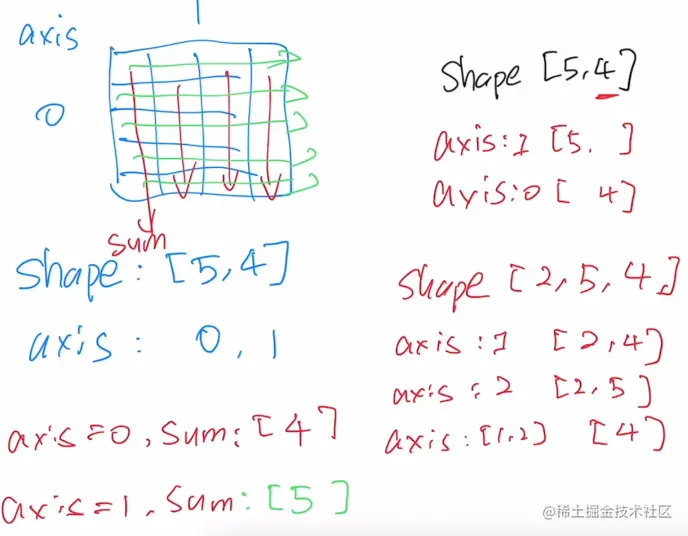
A.sum()
axis从0开始
A.sum(axis=1)
矩阵乘向量
torch.mv(A,x)
矩阵乘法
torch.mm(A,B)
范数(标量)
向量的范数
L1范数
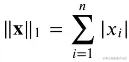
torch.abs(u).sum()
L2范数
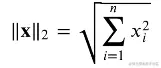
torch.norm(a)
矩阵的范数
佛罗贝尼乌斯范数(矩阵元素的平方和的平方根)
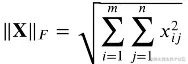
torch.norm(torch.ones(4,9))
矩阵的每一行和列向量做内积(乘法)