(4条消息) Java二叉树理解与重建二叉树题目_学习微站的博客-CSDN博客代码如下实例通过前序遍历和中序遍历得到

 * 二叉树
 * 又称二叉查找树/二叉搜索树
 * 树的查找和搜索功能体现的淋漓尽致
 * 1 定义：二叉树是树的特殊结构，“二”：每个节点最多只能有两个子节点
 * 树可以有n个子节点，教材看到的大多数是二叉树，所以有的人会混淆
 * 刚刚说了二叉树的别称是二叉查找树/二叉搜索树，这是它最重要的功能，去查询
 * 查询---》遍历
 * 按照一定的顺序查找所有的节点
 * 2 数组查找直接根据下标查询
 * 链表把所有的节点遍历查找，直到查到结束
 * 3 树花样多，前序遍历、中序遍历、后序遍历
 * 前序遍历：根 左 右
 * 中序遍历：左 根 右
 * 后序遍历：左 右 根
 * 左一定在右前面，遍历命名的依据根据跟节点的查询顺序来定
 * 4 实现方法是递归和循环，递归简洁、循环效率高
 * 还有宽度优先遍历 从第一层到最后一层去查询，从上到下
 * 二叉树两个特例是堆和红黑树 堆有最大堆，最小堆，快速找最大值和最小值，红黑树 集合set,map会用

代码如下
实例
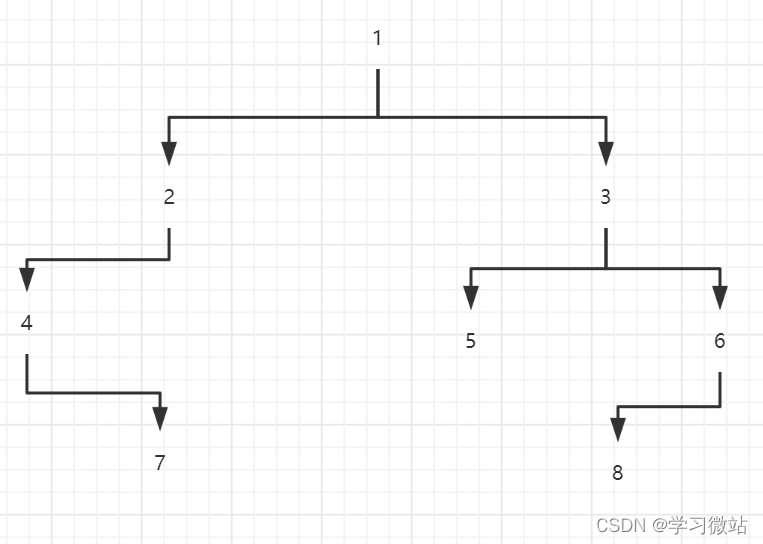
通过前序遍历和中序遍历得到二叉树
在这里插入图片描述

package tree;

/**
 * @author kegekeqi
 * @version 1.0
 * @date 2021-12-12 9:50
 */
public class TreeNode {
	int val;
	TreeNode left;
	TreeNode right;
	TreeNode(int x) {
		val = x;
	}

	@Override
	public String toString() {
		return "TreeNode{" +
				"val=" + val +
				", left=" + left +
				", right=" + right +
				'}';
	}
}

package tree;

/**

@author kegekeqi
@version 1.0
@date 2021-12-12 9:25 / public class BinaryTree { /*
- 二叉树
- 又称二叉查找树/二叉搜索树
- 树的查找和搜索功能体现的淋漓尽致
- 1 定义：二叉树是树的特殊结构，“二”：每个节点最多只能有两个子节点
- 树可以有n个子节点，教材看到的大多数是二叉树，所以有的人会混淆
- 刚刚说了二叉树的别称是二叉查找树/二叉搜索树，这是它最重要的功能，去查询
- 查询---》遍历
- 按照一定的顺序查找所有的节点
- 2 数组查找直接根据下标查询
- 链表把所有的节点遍历查找，直到查到结束
- 3 树花样多，前序遍历、中序遍历、后序遍历
- 前序遍历：根左右
- 中序遍历：左根右
- 后序遍历：左右根
- 左一定在右前面，遍历命名的依据根据跟节点的查询顺序来定
- 4 实现方法是递归和循环，递归简洁、循环效率高
- 还有宽度优先遍历从第一层到最后一层去查询，从上到下
- 二叉树两个特例是堆和红黑树堆有最大堆，最小堆，快速找最大值和最小值，红黑树集合set,map会用 */
public TreeNode reConstructBinaryTree(int[] pre, int[] in) { if (null == pre || pre.length == 0 || null == in || in.length == 0 || pre.length != in.length) { return null; } return construct(pre, in, 0, pre.length - 1, 0, in.length - 1); }

private TreeNode construct(int[] pre, int[] in, int preStart, int preEnd, int inStart, int inEnd) { if (preStart > preEnd || inStart > inEnd) { return null; } TreeNode node = new TreeNode(pre[preStart]); int inMid = inStart; while (in[inMid] != pre[preStart]) { inMid ++; } int delta = inMid - inStart; node.left = construct(pre, in, preStart + 1, preStart + delta, inStart, inMid - 1); node.right = construct(pre, in, preStart + delta + 1, preEnd, inMid + 1, inEnd); return node; }

}

package tree;

/**
 * @author kegekeqi
 * @version 1.0
 * @date 2021-12-12 9:59
 */
public class Main {
	public static void main(String[] args) {
		BinaryTree binaryTree = new BinaryTree();
		//前序遍历
		int[] pre = {1, 2, 4, 7, 3, 5, 6, 8};
		//中序遍历
		int[] in = {4, 7, 2, 1, 5, 3, 8, 6};
		TreeNode node = binaryTree.reConstructBinaryTree(pre, in);
		System.out.println(node);
	}
}


```

测试结果：

```
TreeNode
{
    val = 1, left = TreeNode
    {
        val = 2, left = TreeNode
        {
            val = 4, left = null, right = TreeNode
            {
                val = 7, left = null, right = null
            }
        }, right = null
    }, right = TreeNode
    {
        val = 3, left = TreeNode
        {
            val = 5, left = null, right = null
        }, right = TreeNode
        {
            val = 6, left = TreeNode
            {
                val = 8, left = null, right = null
            }, right = null
        }
    }
}

```

这个例子中得到最终确定的树结构，是输入前序遍历、中序遍历的数组得到的  
![在这里插入图片描述](https://img-blog.csdnimg.cn/1a4d7526cffc40d29bb9792784ff4d8f.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5a2m5Lmg5b6u56uZ,size_20,color_FFFFFF,t_70,g_se,x_16)

> 本文使用 [文章同步助手](https://juejin.cn/post/6940875049587097631) 同步