开启掘金成长之旅！这是我参与「掘金日新计划 · 12 月更文挑战」的第3天，点击查看活动详情

---

一、复杂度函数的阶

我们可以用函数的阶数来形象地描绘函数之间增长快慢的关系。

1.1 同阶函数集合

定义函数$f(n)$的同阶函数集合$\Theta (f(n))$为：

即：从某一项起，$f(n)$的线性范围内的函数的集合。

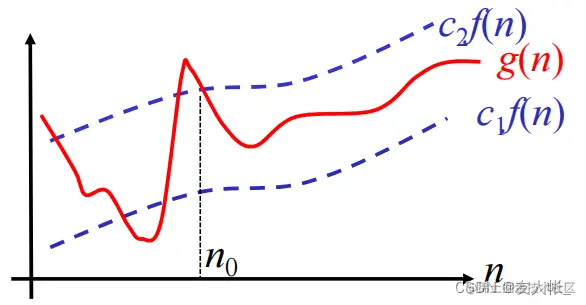
注意：

• $g(n)\in \Theta (f(n))$常记为$g(n)=\Theta (f(n))$，称$g(n)$与$f(n)$同阶

定理：

1.2 低阶函数集合

定义函数$f(n)$的低阶函数集合$O(f(n))$为：

即：从某一项起，始终小于$f(n)$的线性倍数的函数的集合。

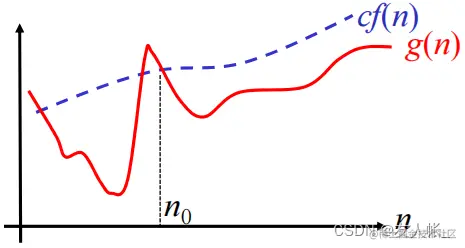
注意：

• $g(n)\in O(f(n))$常记为$g(n)=O(f(n))$，称$f(n)$是$g(n)$的上界

1.3 高阶函数集合

定义函数$f(n)$的高阶函数集合$\Omega (f(n))$为：

即：从某一项起，始终大于$f(n)$的线性倍数的函数的集合。

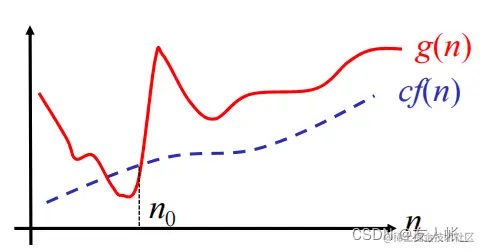
注意：

• $g(n)\in \Omega(f(n))$常记为$g(n)=\Omega(f(n))$，称$f(n)$是$g(n)$的下界

1.4 严格低阶函数集合

定义函数$f(n)$的严格低阶函数集合$o(f(n))$为：

即：对于任意的正实数倍数的$f(n)$，从某一项开始，该函数总在其下方。

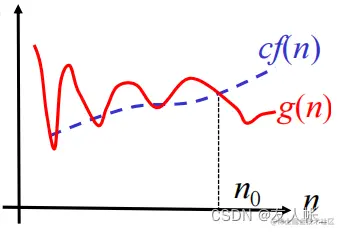
注意：

• $g(n)\in o (f(n))$常记为$g(n)=o (f(n))$，称$f(n)$是$g(n)$的严格上界

定理：

1.5 严格高阶函数集合

定义函数$f(n)$的严格高阶函数集合$\omega (f(n))$为：

即：对于任意的正实数倍数的$f(n)$，从某一项开始，该函数总在其上方。

注意：

• $g(n)\in \omega (f(n))$常记为$g(n)=\omega (f(n))$，称$f(n)$是$g(n)$的严格下界

定理：

---

二、函数阶的性质

（1）传递性

（2）自反性

（3）对称性

（4）反对称性

---

三、标准符号和通用函数

3.1 Flour和Ceiling

（1）定义

$\lfloor x\rfloor$表示小于等于x的最大整数，$\lceil x \rceil$表示大于等于x的最小整数。

（2）定理

① $x-1 <\left \lfloor x \right \rfloor \leq x \leq \left \lceil x \right \rceil <x+1$

② $\left \lfloor \frac{n}{2} \right \rfloor + \left \lceil \frac{n}{2} \right \rceil =n,\forall n \in Z$

③ $\begin{matrix}\left \lceil \frac{ \left \lceil \frac{n}{a} \right \rceil}{b} \right \rceil = \left \lceil \frac{n}{ab} \right \rceil \\\left \lfloor \frac{\left \lfloor \frac{n}{a} \right \rfloor}{b} \right \rfloor=\left \lfloor \frac{n}{ab} \right \rfloor \end{matrix} ,\forall a,b,n \in Z, a\ne 0,b \ne 0$

3.2 线性和

给出两个定理：

① $\sum_{k=1}^{n}(ca_k+b_k) = c\sum_{k=1}^{n} a_k + \sum_{k=1}^{n} b_k$

② $\sum_{k=1}^{n}\theta (f(k))= \theta (\sum_{k=1}^{n}f(k))$