0 论文信息

1 背景介绍

简而言之就是在 IRM 的基本框架下，我们的目标是设计一个接近于发现因果特征的合理化标准。虽然评估因果关系具有挑战性，但我们可以通过搜索在某种意义上不变的特征来近似完成任务。其主要思想是通过将数据划分到不同的环境中来突出虚假(非因果)变化。同样的预测器，如果基于因果特征，应该在不同的环境中保持最佳。~~一言以蔽之就是在 IRM 的框架下改惩罚项。~~

2 前言 : MMI 及其局限性

2.1 最大互信息准则

MMI 目标可以表述如下。给定输入输出对 $(X,Y)$ ， MMI 的目标是找到一个基本原理 Z，它是 X 的一个屏蔽版本，这样它就可以最大化 Z 和 Y 之间的相互信息。在形式上

\max _{m \in \mathcal{S}} I(Y ; Z) \quad \text { s.t. } Z=m \odot \boldsymbol{X} \tag{1}

其中 m 是二进制掩码，S 表示 $\{0,1\}^N$ 的子集，具有稀疏性和连续性约束。N 是 X 的总长度。我们把约束集 S 的精确数学形式抽象在这里，它将在第3.5节正式介绍。 $\odot$ 表示两个向量或矩阵的元素相乘。由于互信息衡量 Z 对 Y 的预测能力，MMI 本质上试图找到一个输入特征的子集，它可以最好地预测输出 Y。

2.2 MMI 的局限性

MMI 的最大问题是，它容易发现虚假的概率相关性，而不是找到因果解释。

3 对抗不变的合理化

3.1 不变的合理化

作者从互信息的角度给出了该问题的另一个合理化的目标 :

\max _{m \in \mathcal{S}} I(Y ; \boldsymbol{Z}) \quad \text { s.t. } \boldsymbol{Z}=\boldsymbol{m} \odot \boldsymbol{X}, \quad Y \perp E \mid \boldsymbol{Z} \tag{2}

在此 $\perp$ 表示概率独立性。式 (1) 与式 (2) 的唯一区别在于后者具有不变性约束。

3.2 InvRat 框架

式 (2) 中的约束优化很难用原始形式求解。InvRat 引入了一个博弈理论框架，可以近似地解决这一问题。注意，不变性约束可以转换为熵的约束，即

Y \perp E \mid \boldsymbol{Z} \Leftrightarrow H(Y \mid \boldsymbol{Z}, E)=H(Y \mid \boldsymbol{Z})\tag{3}

这意味着如果 Z 是不变的，E 不能提供 Z 以外的额外信息来预测 Y。在这个观点的指导下，InvRat 由三个部分组成，如下图所示

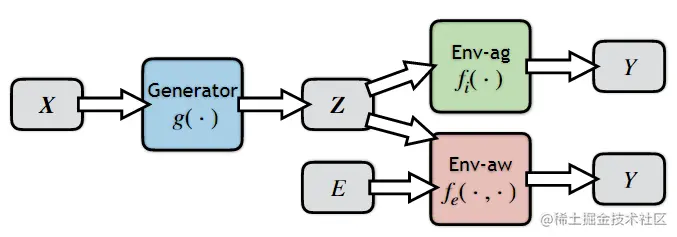
图 1.InvRat 框架有三个组件 : 基本原理生成器 $g(X)$ 、环境不可知预测器 $f_i(Z)$ 和环境感知预测器 $f_e(Z,E)$

环境不可知预测器 $f_i(Z)$ 和环境感知预测器 $f_e(Z,E)$ 的目标是从基本原理 Z 预测 Y。它们之间的唯一区别是后者可以访问 E 作为另一个输入特性，而前者不能。形式上，表示 $\mathcal{L}(Y;F)$ 为单个实例的交叉熵损失。那么这两个预测因子的学习目标可以写成 :

\mathcal{L}_i^*=\min _{f_i(\cdot)} \mathbb{E}\left[\mathcal{L}\left(Y ; f_i(\boldsymbol{Z})\right)\right], \mathcal{L}_e^*=\min _{f_e(\cdot, \cdot)} \mathbb{E}\left[\mathcal{L}\left(Y ; f_e(\boldsymbol{Z}, E)\right)\right] \tag{4}

其中 $Z=g(X)$ 。基本原理生成器通过屏蔽 X 生成 Z。基本原理生成器的目标也是最小化不变性预测损失 $\mathcal{L}_i^*$ 。然而，还有一个额外的目标是使 $\mathcal{L}_i^*$ 和 $\mathcal{L}_e^*$ 之间的差距变小。形式上，生成器的目标如下 :

\min _{g(\cdot)} \mathcal{L}_i^*+\lambda h\left(\mathcal{L}_i^*-\mathcal{L}_e^*\right) \tag{5}

其中 $h(t)$ 为凸函数，当 $t<0$ 时单调递增，当 $t\ge0$ 时严格单调递增，例如 $h(t)=t$ 和 $h(t) = \text{ReLU}(t)$ 。

3.3 收敛性质

本节证明 (4) 和(5) 式可以解 (2) 式的拉格朗日形式。如果 $f_i(\cdot)$ 和 $f_e(\cdot,\cdot)$ 的表示幂足够大，则交叉熵损失可以达到其熵下限，即 :

\mathcal{L}_i^*=H(Y \mid Z), \quad \mathcal{L}_e^*=H(Y \mid Z, E)

注意，环境意识损失不应大于环境不可知损失，因为可以获得更多的信息，即 $H(Y \mid Z) \geq H(Y \mid Z, E)$ ，为了满足 KKT 优化条件我们进行如下转换 :

H(Y \mid Z)=H(Y \mid Z, E) \Leftrightarrow H(Y \mid Z) \leq H(Y \mid Z, E) \tag{6}

最后，注意 $I(Y ; Z)=H(Y)-H(Y \mid Z)$ 。因此，式 (5) 中的目标可以看作式 (2) 的拉格朗日形式，将约束改写为不等式约束

h(H(Y \mid Z)-H(Y \mid Z, E)) \leq h(0) \tag{7}

根据 KKT 条件，式 (7) 绑定时 $\lambda>0$ 。此外，式 (4) 和式 (5) 中的目标可以重写为极大极小对策

\min _{\left.g(\cdot), f_i(\cdot)\right)} \max _{f_e(\cdot \cdot \cdot)} \mathcal{L}_i\left(g, f_i\right)+\lambda h\left(\mathcal{L}_i\left(g, f_i\right)-\mathcal{L}_e\left(g, f_e\right)\right)\tag{8}

3.4 不变性和泛化性

3.5 结合稀疏性和连续性约束

这两部分没有太多公式和理论，在此不多赘述。

4 实验

这篇文章的工作主要是聚焦于 NLP 相关领域和问题，实际上所使用的对抗是假对抗，因为掩码一开始就一块传了进去。个人觉得这也是一个稍微令人遗憾的地方。

5 总结

一开始看得很疑惑，因为之前没有学过信息论，~~但实际感觉这个互信息就是用来讲故事的~~，整个框架的结果还是有一种简洁的美 (以及并没有像 IRMv1 那样限定在线性情况，但是没有像 IRMv1 那样有完备的理论支撑)。同时，个人感觉这个对抗性其实大有可为 (想到之前迁移学习的那个 MCD_DA 框架就是使用对狂取得了很好的效果)。

Invariant Rationalization 论文阅读