梯度法

Gavin_Bowl
157 阅读3分钟

1.梯度法

负梯度是一个可微函数的局部最速下降方向，沿此方向可以快速找到局部极小点。

梯度法
选择 x0∈Rnx_0 \in \mathbb{R}^n.
迭代xk+1=xk−hk∇f(xk)x_{k+1} = x_{k} - h_k \nabla f(x_k), k = 0,1,2,...

其中hkh_k为步长，它必须为正数。

2.步长选择策略

有如下几种策略：
1.预先选择序列{hk}k=0∞\{ h_k \}^{\infty}_{k=0},例如

hk=hhk=hk+1\begin{aligned} h_k &= h \\ h_k &= \frac{h}{\sqrt{k+1}} \end{aligned}

2.全松弛(精确步长)

hk=arg  minh≥0f(xk−h∇f(xk))h_k = arg \; \underset{h \ge 0}{min} f(x_k - h \nabla f(x_k))

3.Amijo\mathbf{Amijo}规则：对h>0h > 0，确定xk+1=xk−h∇f(xk)x_{k+1} = x_k - h \nabla f(x_k)，满足

α⟨∇f(xk),xk−xk+1⟩≤f(xk)−f(xk+1)(1.2.16)\alpha \langle \nabla f(x_k) , x_k - x_{k+1} \rangle \le f(x_k) - f(x_{k+1}) \tag{1.2.16}
β⟨∇f(xk),xk−xk+1⟩≥f(xk)−f(xk+1)(1.2.17)\beta \langle \nabla f(x_k) , x_k - x_{k+1} \rangle \ge f(x_k) - f(x_{k+1}) \tag{1.2.17}

其中0<α<β<10 < \alpha < \beta < 1.

第一种策略是最简单的，也常用于各种教材当中。
第二种策略是理论上的，实际上无法应用，因为即便在一维的情况下也无法在有限时间内找到最小的h
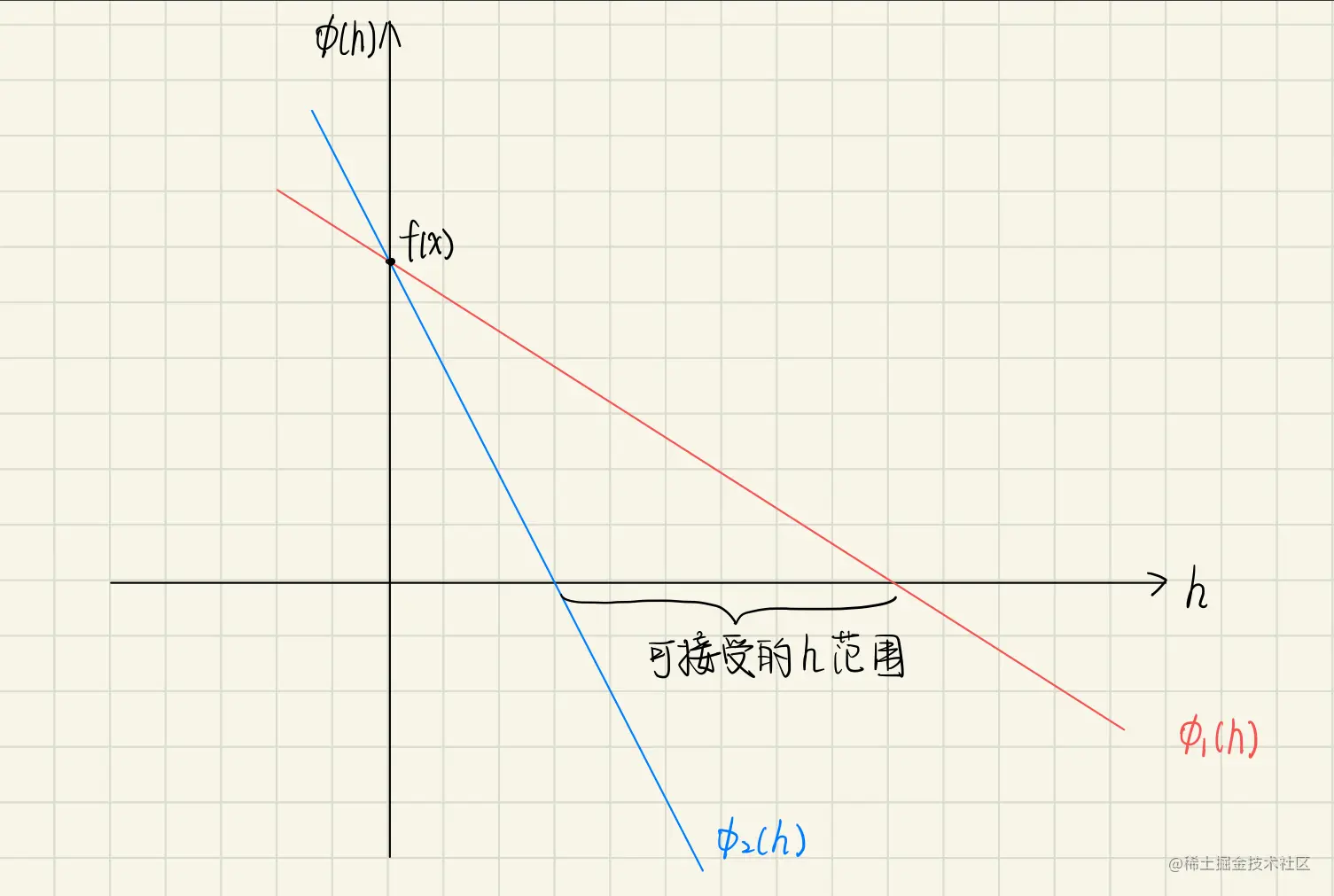
第三种策略用于很多实际的算法，从几何的角度来解释，取x∈Rnx \in \mathbb{R}^n且∇f(x)≠0\nabla f(x) \neq 0时，考虑关于h的函数:

ϕ(h)=f(x−h∇f(x)),h≥0\phi(h) = f(x - h \nabla f(x)), h \ge 0

于是该策略可接受的步长介于下面两个线性函数之间：

ϕ1(h)=f(x)−αh∣∣∇f(x)∣∣2ϕ2(h)=f(x)−βh∣∣∇f(x)∣∣2\phi_1(h) = f(x) - \alpha h ||\nabla f(x)||^2 \\ \phi_2(h) = f(x) - \beta h ||\nabla f(x)||^2

这两个函数由(1.2.16)和(1.2.17)消去xk+1x_{k+1}得到。

F7FE2F7B670AE141BA2D2062766313B4.png

3.步长的最优选择

我们考虑y=x−h∇f(x)y = x-h \nabla f(x)，依据一些已有的结论公式，有

f(y)≤f(x)+⟨∇f(x),y−x⟩+L2∣∣y−x∣∣2=f(x)−h∣∣∇f(x)∣∣2+h22L∣∣∇f(x)∣∣2=f(x)−h(1−h2L)∣∣∇f(x)∣∣2(1.2.19)\begin{aligned} f(y) &\le f(x) + \langle \nabla f(x),y-x \rangle + \frac{L}{2}||y-x||^2 \\ &= f(x) - h||\nabla f(x)||^2 + \frac{h^2}{2}L||\nabla f(x)||^2 \\ &= f(x) - h(1-\frac{h}{2}L)||\nabla f(x)||^2 \tag{1.2.19} \end{aligned}

由此，我们希望得到一个f(y)f(y)的最优上界 对应如下的一维问题：

Δ(h)=−h(1−h2L)→minh\Delta(h) = -h(1-\frac{h}{2}L) \rightarrow \underset{h}{min}

利用简单的求导知识可以推知h∗=1Lh^* = \frac{1}{L}时取得最佳上界。 此时有

f(y)≤f(x)−12L∣∣∇f(x)∣∣2f(y) \le f(x) - \frac{1}{2L}||\nabla f(x)||^2

对于定长的策略，hk=hh_k = h，接下来的分析就和上述过程一致，
最后推理得到最优的选择为hk=1Lh_k = \frac{1}{L}

对于全松弛策略我们有同样的结论，因为这种策略不会比定长策略差

而对于Armijo\mathbf{Armijo}规则，依据(1.2.17)有

f(xk)−f(xk+1)≤β⟨∇f(xk),xk−xk+1⟩=βhk∣∣∇f(xk)∣∣2f(x_k) - f(x_{k+1}) \le \beta \langle \nabla f(x_k) , x_k - x_{k+1} \rangle = \beta h_k||\nabla f(x_k)||^2

同时由(1.2.19)又能得到

f(xk)−f(xk+1)≥hk(1−hk2L)∣∣∇f(xk)∣∣2f(x_k) - f(x_{k+1}) \ge h_k(1-\frac{h_k}{2}L)||\nabla f(x_k)||^2

结合上述两式，可以得到hk≥2L(1−β)h_k \ge \frac{2}{L}(1-\beta)
同理利用(1.2.16)能够得到

f(xk)−f(xk+1)≥α⟨∇f(xk),xk−xk+1⟩=αhk∣∣∇f(xk)∣∣2f(x_k) - f(x_{k+1}) \ge \alpha \langle \nabla f(x_k) , x_k - x_{k+1} \rangle = \alpha h_k||\nabla f(x_k)||^2

继续与hk≥2L(1−β)h_k \ge \frac{2}{L}(1-\beta)相结合，可以得到

f(xk)−f(xk+1)≥2Lα(1−β)∣∣∇f(xk)∣∣2f(x_k) - f(x_{k+1}) \ge \frac{2}{L} \alpha (1-\beta)||\nabla f(x_k)||^2

综合上述三种策略对应的结论，我们可以一般化地描述一个统一的结论

f(xk)−f(xk+1)≥wL∣∣∇f(xk)∣∣2(1.2.20)f(x_k) - f(x_{k+1}) \ge \frac{w}{L} ||\nabla f(x_k)||^2 \tag{1.2.20}

其中ww是一个正常数

4.性能评估

我们将(1.2.20)式对k=0,1,⋯ ,Nk = 0,1,\cdots,N进行累加，可以得到

wL∑k=0N∣∣∇f(xk)∣∣2≤f(x0)−f(xN+1)≤f(x0)−f∗(1.2.21)\frac{w}{L} \sum^N_{k=0}||\nabla f(x_k)||^2 \le f(x_0) - f(x_{N+1}) \le f(x_0) - f^* \tag{1.2.21}

其中f∗f^*是函数局部最小值 由上述式子可以得知左式是有界的，那么

∣∣∇f(xk)∣∣→0      当k→∞时||\nabla f(x_k)|| \rightarrow 0 \; \; \; 当k \rightarrow \infty 时

我们先做出如下定义

gN∗=min0≤k≤N∣∣∇f(xk)∣∣g^*_N = \underset{0 \le k \le N}{min} ||\nabla f(x_k)||

其含义就是所有不同k中最小的梯度 结合(1.2.21)可以得到

gN∗≤1N+1[1wL(f(x0)−f∗)]12(1.2.22)g^*_N \le \frac{1}{\sqrt{N+1}}[\frac{1}{w}L(f(x_0)-f^*)]^{\frac{1}{2}} \tag{1.2.22}

该式子可以描述∣∣∇f(xk)∣∣||\nabla f(x_k)||收敛的速率。

5.举个例子

考虑两个变量的函数

f(x)=f(x1,x2)=12x12+14x24−12x22f(x) = f(x_1,x_2) = \frac{1}{2} x_1^2 + \frac{1}{4} x_2^4 - \frac{1}{2} x_2^2

求出该函数的梯度为∇f(x)=(x1,x23−x2)T\nabla f(x) = (x_1,x_2^3-x_2)^T。
于是可见有三个点满足梯度为0

x1∗=(0,0),  x2∗=(0,−1),  x3∗=(0,1)x_1^* = (0,0),\; x_2^* = (0,-1),\; x_3^* = (0,1)

这三个点可能是函数的局部极小值。接着计算Hessian矩阵

Hessian矩阵

H=[∂2F∂x12∂F∂x1∂x2⋯∂F∂x1∂xn∂2F∂x2∂x1∂F∂x22⋯∂F∂x2∂xn⋮⋮⋱⋮∂2F∂xn∂x1∂F∂xn∂x2⋯∂F∂xn2]H = \begin{bmatrix} \frac {\partial^2F} {\partial x_1^2} & \frac {\partial^F} {\partial x_1 \partial x_2} & \cdots & \frac {\partial^F} {\partial x_1 \partial x_n} \\ \frac {\partial^2F} {\partial x_2 \partial x_1} & \frac {\partial^F} {\partial x_2^2} & \cdots & \frac {\partial^F} {\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac {\partial^2F} {\partial x_n \partial x_1} & \frac {\partial^F} {\partial x_n \partial x_2} & \cdots & \frac {\partial^F} {\partial x_n^2} \end{bmatrix}

用于判定极值点
当Hessian矩阵正定时，任意向量v有vTHv>0v^T H v > 0，为极小值点
当Hessian矩阵负定时，任意向量v有vTHv<0v^T H v < 0，为极大值点
当Hessian矩阵同时具有正负特征值时，该点为鞍点。

于是此处的Hessian矩阵为

∇2f(x)=[1003x22−1]\nabla^2 f(x) = \begin{bmatrix} 1 & 0 \\ 0 & 3x_2^2 - 1 \end{bmatrix}

于是点x2∗,x3∗x_2^*,x_3^*代入矩阵为正定的，是局部最小值，而x1∗x_1^*则为鞍点。

接下来考虑从(1,0)出发的梯度算法路径，会发现无论怎么走第二个坐标恒为0，最终将会收敛到x1∗x_1^*，由此可见，缺乏约束的情况下，梯度法只能靠近一个稳定点。

参考资料

[1] Lectures on Convex Optimization(Second Edition)
[2] Hessian矩阵

avatar
文章
阅读
粉丝