Haskell to Core:通过解构了解Haskell的特性这篇文章是基于我在2020年Haskell Love大会

这篇文章是基于我在2020年Haskell Love大会上的同名演讲，我在演讲中粗略地介绍了GHC的前端管道、内部Core语言和desugaring pass。

Haskell是一种具有许多特性的表达式语言。一方面，它使Haskell变得很方便，为程序员配备了丰富的工具库，以完成工作并编写高质量的软件。另一方面，培养对这些工具和所有语言特性的透彻理解，需要时间、努力和经验。

建立对语言特征的直觉的一个方法是使用它。实践出真知，通过试验和错误，你可以发现使用语言的某些部分的来龙去脉。然而，以这种方式获得的知识可能是肤浅的，心智模型也只能达到手头任务的需要。

更深入的洞察力来自于不同的角度：你需要将一个概念分解成其基本的组成成分。例如，什么是多参数函数？在诅咒语言中，我们知道\a b c -> ... ，与\a -> \b -> \c -> ... 。因此，我们已经把多参数函数的概念简化为单参数函数的更简单的概念。

对于一个更复杂的例子：什么是do-notation？为了掌握它，你需要思考它是如何被去掉符号，变成>>= 和>> （还有<*> 与-XApplicativeDo ）。

那么infix运算符、if-then-else表达式、列表理解、类型类、类型族、GADTs呢？有多少Haskell是必不可少的，又有多少是上面的糖？

如果我们开始思考Haskell程序被解构为GHC核心的方式，这一点就会变得很清楚：一种小而优雅的语言，在GHC的编译管道中被用作中间表示。Haskell的许多特性都可以被还原为Core的少数结构。

解ugaring的本质

解构将一个使用许多不同语言结构的程序翻译成一个只使用少数结构的程序。

例如，考虑这个片段：

product [a + b, c + d]

它使用了几个Haskell特性：

Lists literals:[a, b, c, ...]
操作符的应用。x # y
函数的应用。f x

但我们可以把它改写成只使用函数应用：

product (
  (:) ((+) a b) (
  (:) ((+) c d) (
  [])))

诚然，最终的结果并不那么可读。但是用来写这个程序的构件更简单，这才是最重要的一点。

解构的内涵

解构不仅仅是一个抽象的概念：它是GHC管道的一个具体步骤。每个Haskell程序在编译过程中都会被解构为Core。因此，为了看清全貌，考虑一下解构之前的步骤是有帮助的。

编译器的输入是一个字符串，一个字符序列：

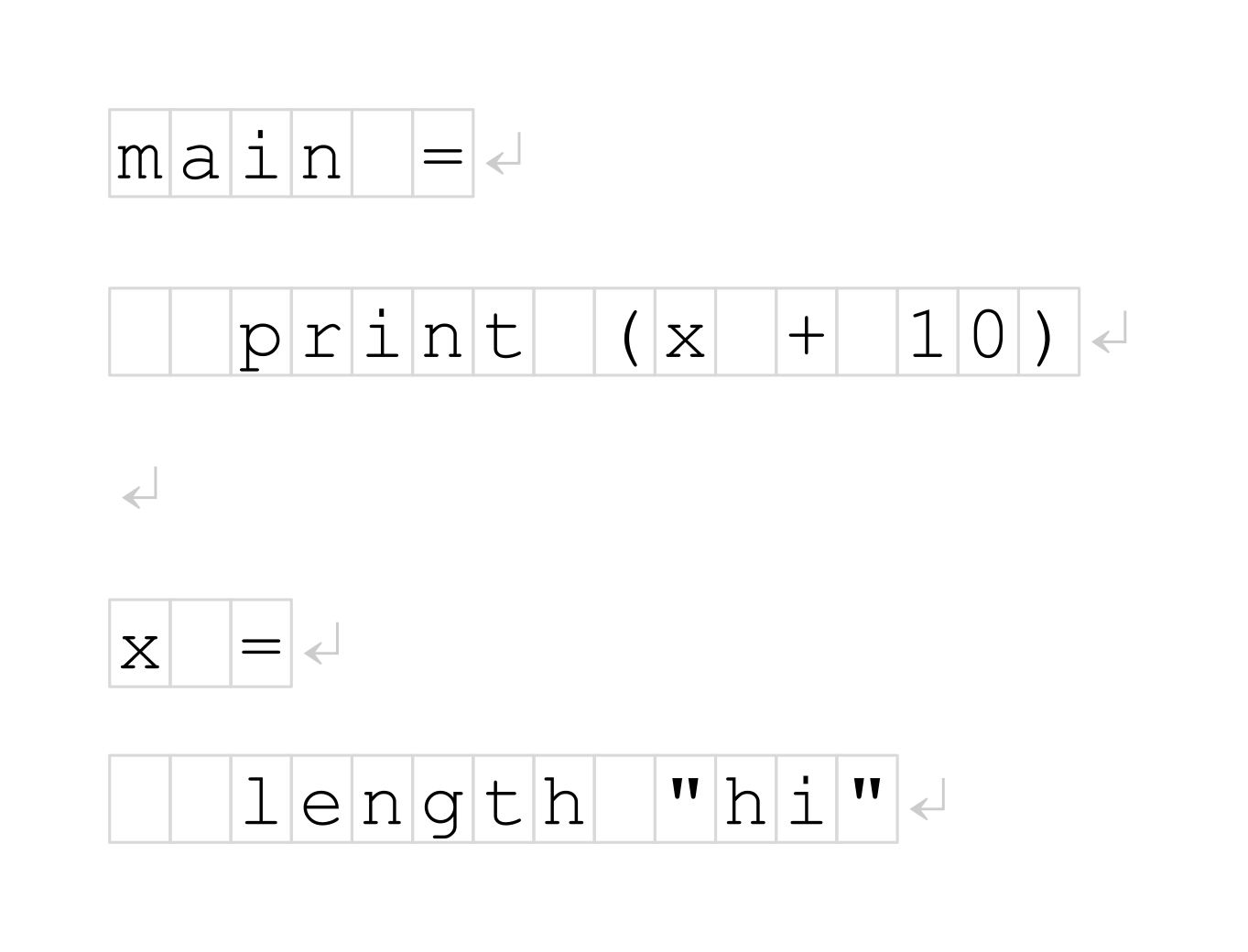
Parser Input

要从哪里开始处理这个序列呢？实际上，这一点是众所周知的。第一步是词法分析，将这些字符的子序列分组为有标签的标记：

Lexer Output

然后这些标记被组织成一棵树。这就是句法分析：

Parser Output

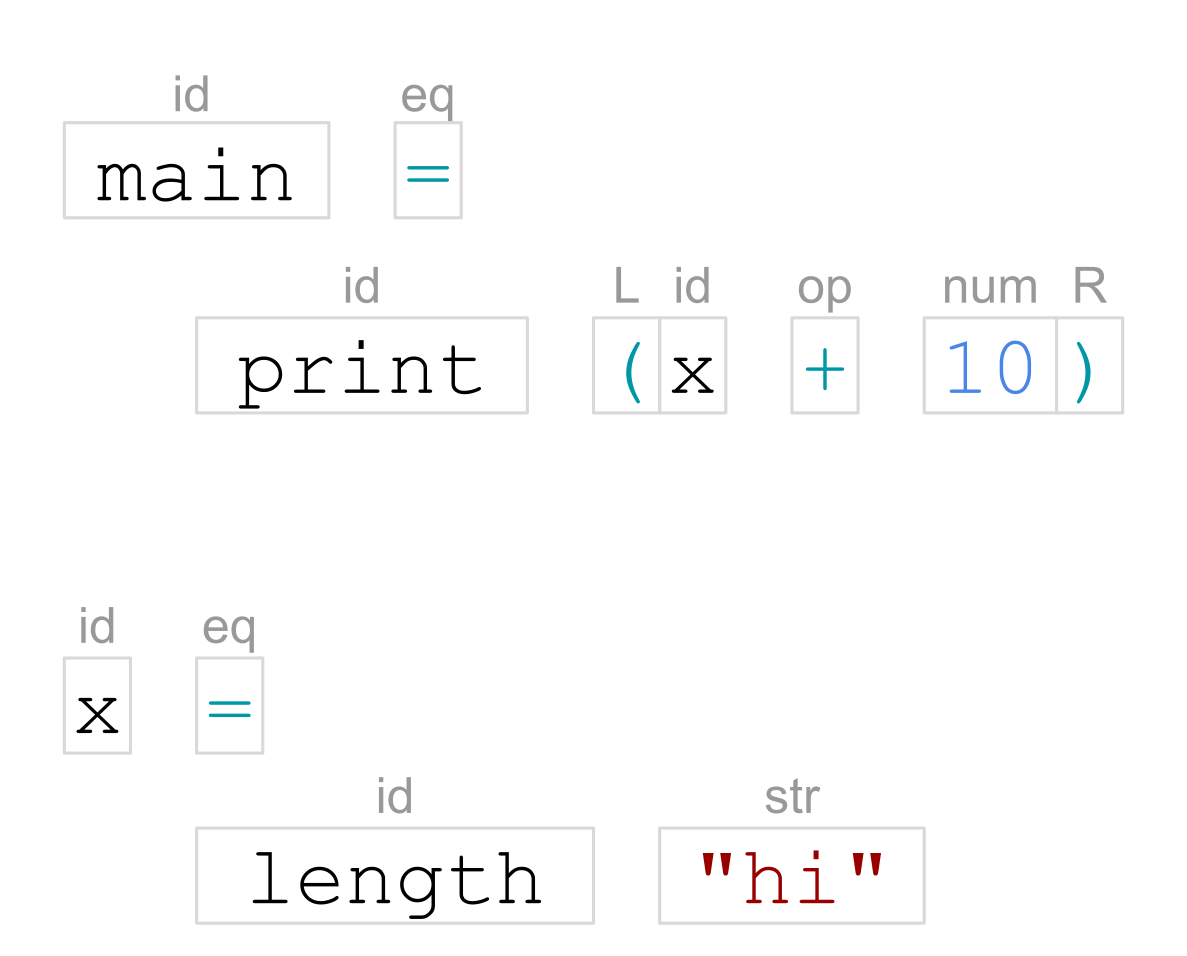
这个树的结构取决于我们所使用的语言。在Haskell中，一个模块包含声明，如数据声明、类声明、函数/变量定义，等等。在这个例子中，我们有两个值绑定，标记为'bind'。

在'绑定'中，左边有一个模式，右边有一个表达式。在这个例子中，模式是简单的变量名，但是我们也可以有作为模式、视图模式、对特定数据构造器的匹配，等等。

一个表达式可以是多种形式之一，但在这里我们有：

app'--函数应用，由一个函数和其参数组成。
'op app' - 操作符的应用，由两个操作数和一个操作符组成。
'var' - 对其他命名值的引用。
lit'--数字和字符串字面。

然后我们进行名称解析，找出哪个名称指的是什么。

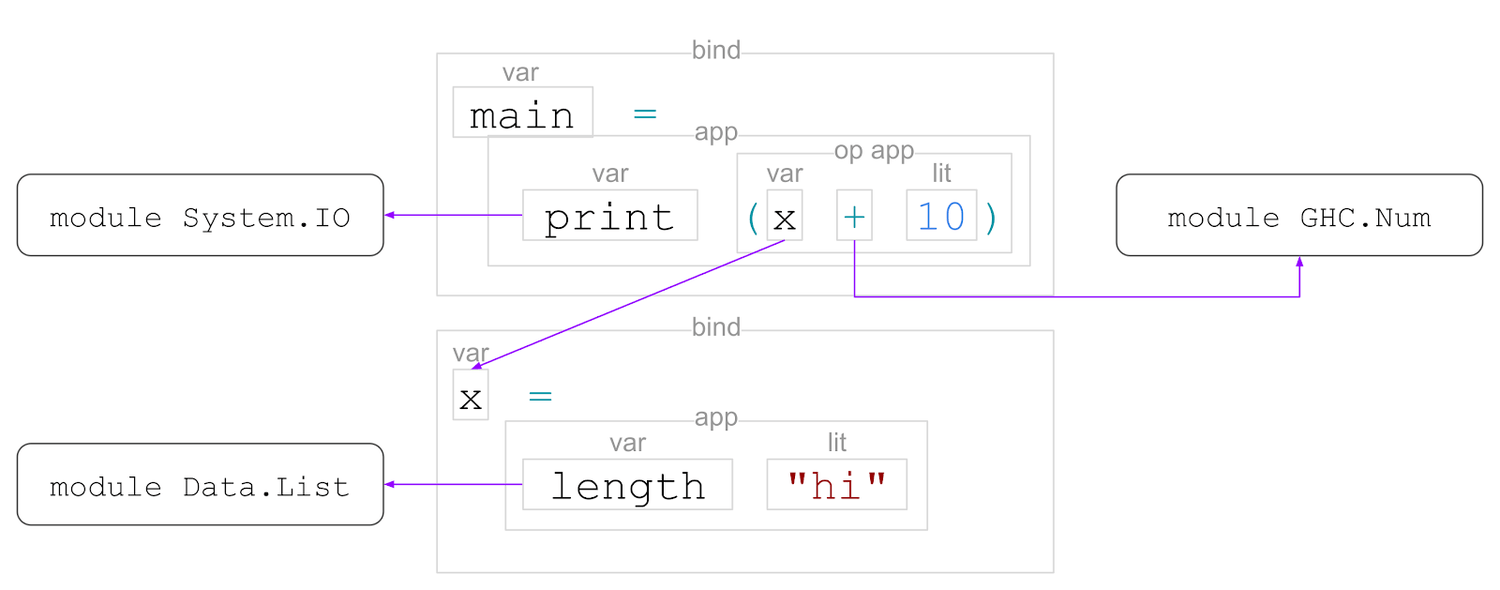
Renamer Output

这里，'print'、'+'和'length'是从其他模块导入的，而'x'是在同一个模块中定义的。

然后，我们分析程序，检查并推断其表达式和子表达式的类型：

main :: IO ()
x :: Int

这就是GHC的流水线，或者至少是它的前端：

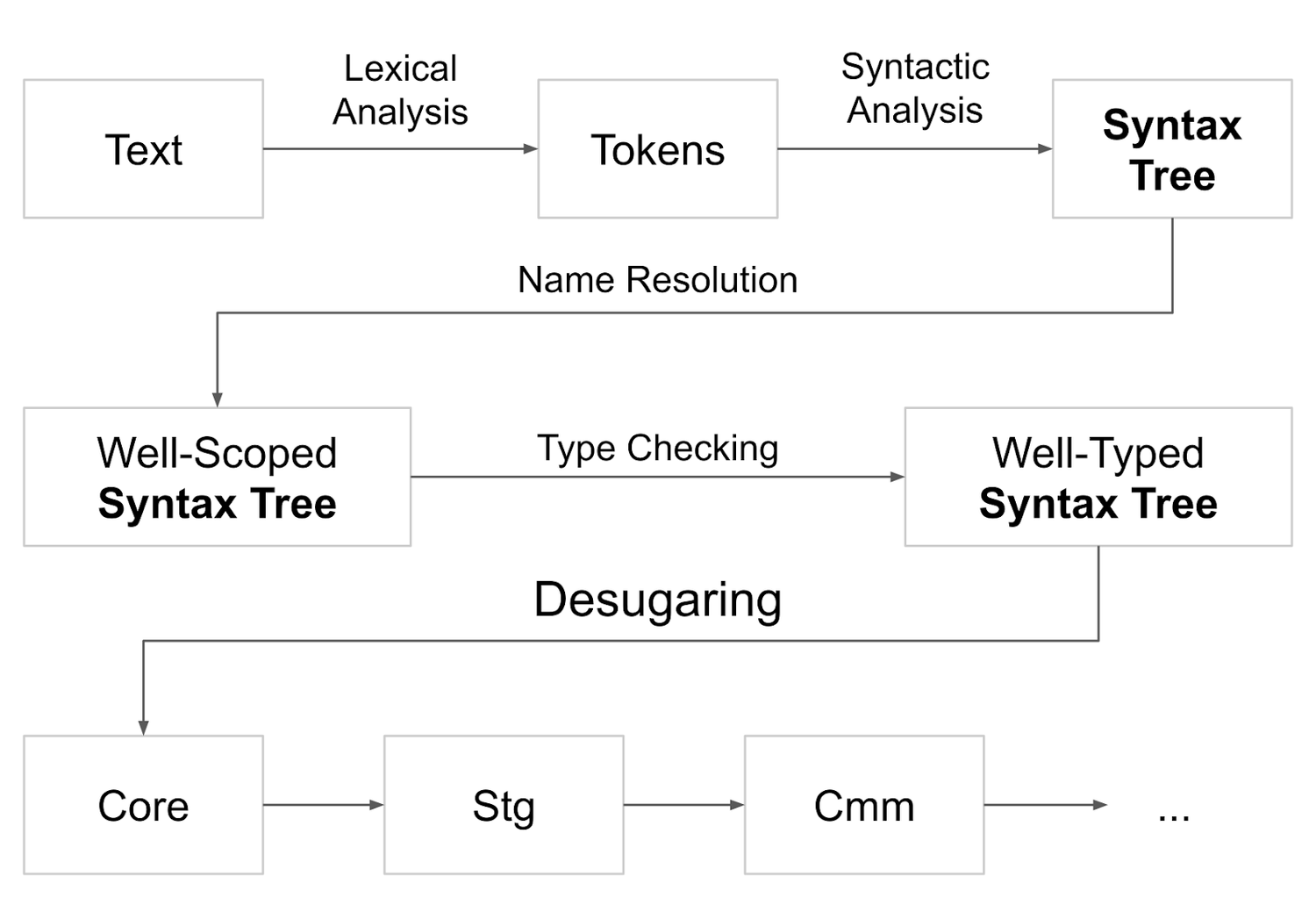
GHC pipeline

文本到令牌。
标记到一个语法树。
在语法树上添加范围信息。
将类型信息添加到语法树中。

这就给我们留下了一个范围良好、类型良好的语法树。这就是解构的输入。而输出则是Core程序，Core是一种类似于Haskell的语言，但它更小，功能更少。

Core的简单性

为了理解Core如何更简单，让我们先深入了解一下Haskell。为了表示一个Haskell表达式，GHC定义了一个叫做HsExpr 的类型。如果你打开 [compiler/GHC/Hs/Expr.hs](https://gitlab.haskell.org/ghc/ghc/-/blob/master/compiler/GHC/Hs/Expr.hs)在GHC的源代码中，你会看到它：

data HsExpr p
  = HsVar ...         --   v
  | HsLit ...         --   "hello"
  | HsApp ...         --   f x
  | OpApp ...         --   x # y
  | ...

还记得句法分析如何为每个子表达式创建一个节点吗？而这些节点可以是不同种类的，如函数应用、运算符应用、变量、字面意义等？HsExpr ，每个节点类型都有一个构造器。HsVar,HsLit,HsApp,OpApp, 等等。

而且有很多很多的节点类型：

data HsExpr p
  = HsVar ...         --   v
  | HsLit ...         --   "hello"
  | HsApp ...         --   f x
  | OpApp ...         --   x # y
  | HsAppType ...     --   f @t
  | HsLam ...         --   \a b c -> d
  | HsLet ...         --   let { v1 = e1; ... } in b
  | ExprWithTySig ... --   e :: t
  | ExplicitList ...  --   [a, b, c, ...]
  | SectionL ...      --   (x #)
  | SectionR ...      --   (# y)
  | ExplicitTuple ... --   (a, b, c)
  | HsCase ...        --   case e of { p1 -> e1; ... }
  | HsLamCase ...     --   \case { p1 -> e1; ... }
  | HsIf ...          --   if c then a else b
  | HsMultiIf ...     --   if { | c1 -> a1 | ... }
  | HsDo ...          --   do { v1 <- e1; e2; ... }
  | RecordCon ...     --   MkR { a1 = e1; ... }
  | RecordUpd ...     --   myR { a1 = e1; ... }
  | ArithSeq ...      --   [a, b .. z]
  | HsPar ...         --   (expr)
  | NegApp ...        --   -x
  | HsBracket ...     --   [| ... |]
  | HsSpliceE ...     --   $( ... )
  | HsProc ...        --   proc v -> do { a1 <- e1 -< v1; ... }
  | HsStatic ...      --   static e
  | HsOverLabel ...   --   #lbl
  | ...

而这仅仅是表达式。还有一些模式，定义在 [compiler/GHC/Hs/Pat.hs](https://gitlab.haskell.org/ghc/ghc/-/blob/master/compiler/GHC/Hs/Pat.hs):

data Pat p
  = WildPat ...       --   _
  | VarPat ...        --   v
  | LazyPat ...       --   ~p
  | BangPat ...       --   !p
  | AsPat ...         --   x@p
  | ParPat ...        --   (p)
  | ListPat ...       --   [a, b, c, ...]
  | TuplePat ...      --   (a, b, c, ...)
  | ConPat ...        --   MkT p1 p2 p3 ...
  | ViewPat ...       --   (f -> p)
  | LitPat ...        --   "hello"
  | SigPat ...        --   p :: t
  | NPat ...          --   42
  | NPlusKPat ...     --   n+42
  | SplicePat ...     --   $( ... )
  | ...

和类型，定义在 [compiler/GHC/Hs/Type.hs](https://gitlab.haskell.org/ghc/ghc/-/blob/master/compiler/GHC/Hs/Type.hs):

data HsType p
  = HsForAllTy ...    --   forall a b c. t
  | HsQualTy ...      --   ctx => t
  | HsTyVar ...       --   v
  | HsAppTy ...       --   t1 t2
  | HsAppKindTy ...   --   t1 @k1
  | HsFunTy ...       --   t1 -> t2
  | HsListTy ...      --   [t]
  | HsTupleTy ...     --   (a, b, c, ...)
  | HsOpTy ...        --   t1 # t2
  | HsParTy ...       --   (t)
  | HsIParamTy ...    --   ?x :: t
  | HsStarTy ...      --   *
  | HsKindSig ...     --   t :: k
  | HsSpliceTy ...    --   $( ... )
  | HsTyLit ...       --   "hello"
  | HsWildCardTy ...  --   _
  | ...

在 [compiler/GHC/Hs/Decls.hs](https://gitlab.haskell.org/ghc/ghc/-/blob/master/compiler/GHC/Hs/Decls.hs)中，有数据声明、类、类型族、实例等等：

data TyClDecl p
  = FamDecl ...       --  type family T
  | SynDecl ...       --  type T = ...
  | DataDecl ...      --  data T = ...
  | ClassDecl ...     --  class C t where ...

data InstDecl p
  = ClsInstD ...      -- instance C T where ...
  | DataFamInstD ...  -- data instance D T = ...
  | TyFamInstD ...    -- type instance F T = ...

当然，这还不是全部。你可以浏览compiler/GHC/Hs/... ，以看到更多。

那Core呢？这是其语法的全部内容：

data Expr
  = Var   Id
  | Lit   Literal
  | App   Expr Expr
  | Lam   Var Expr
  | Let   Bind Expr
  | Case  Expr Var Type [Alt]
  | Cast  Expr Coercion
  | Type  Type
  | Coercion Coercion
  | Tick  ...  -- unimportant

type Alt = (AltCon, [Var], Expr)

data AltCon
  = DataAlt DataCon
  | LitAlt  Literal
  | DEFAULT

data Bind
  = NonRec Var Expr
  | Rec [(Var, Expr)]

data Type
  = TyVarTy Var
  | AppTy Type Type
  | TyConApp TyCon [Type]
  | ForAllTy TyCoVarBinder Type
  | FunTy Mult Type Type
  | LitTy TyLit
  | CastTy Type Coercion
  | CoercionTy Coercion

它的表达式语法只有九个结构：

变量 (Var)
字面意义 (Lit)
函数应用 (App)
lambdas (Lam)
let-bindings (Let)
case-expressions (Case)
cast (Cast)
coercions (Coercion)

如果你知道这些是什么，你就知道Core。如果你既知道Core，又知道Haskell程序是如何被解构到其中的，那么你就可以很容易地推理出Haskell语言的各种特性。

乍一看，你可以把Core看作是Haskell的一个子集，再加上coercions（和cast，这两个是密切相关的）。但这并不是故事的全部。例如，在严格性方面也有区别，因为Core中的case ，总是严格的。如果你想更深入地了解这个问题，这里有一些资源。

然而，作为一个起点，假设Core是Haskell的一个子集就足够了。

通过实例进行解uging

现在让我们通过具体的例子来看看Haskell程序是如何被转化为Core的。我们将从最基本的功能开始，然后逐步深入到更复杂的功能。

Infix运算符

Infix运算符被翻译成函数应用：

Haskell	核心

a && b

(&&) a b

并没有太多的内容。但请记住，在Core中，所有变量的出现都有类型信息，所以更准确的翻译应该是这样的。

((&&) :: Bool -> Bool -> Bool)
  (a :: Bool)
  (b :: Bool)

然而，更多的时候，我将省略类型注释以节省视觉空间。

函数绑定

Core中的绑定总是在左手边有一个单一的变量名。函数绑定被解构为lambdas。

Haskell	核心

f :: Integer -> Integer
f x = x

f =
  \ (x :: Integer) ->
    (x :: Integer)

另外，没有单独的类型签名。所有的类型信息都是内联存储的。

多参数函数绑定

多参数函数被翻译成嵌套的lambdas。在Core中，所有lambdas都是单参数的。

Haskell	编码

f x y = not x && y

f =
  \(x :: Bool) ->
  \(y :: Bool) ->
     (&&) (not x) y

对于手写的多参数lambdas也是如此。

Haskell	核心

f = \x y -> not x && y

f =
  \(x :: Bool) ->
  \(y :: Bool) ->
     (&&) (not x) y

如果你听说过currying，那么对多参数函数的这种处理方式可能会让你感到熟悉。

模式绑定

模式绑定被分解成几个核心绑定：一个是整个值的绑定，另一个是每个部分的绑定。

Haskell	核心

a :: Integer
b :: Bool
(a, b) = (1, True)

ab = (1, True)

a = case ab of
  (,) x y -> x

b = case ab of
  (,) x y -> y

这些部分是用case-expressions提取的。

操作符部分

操作符部分被解构为lambdas。

Haskell	核心内容

(a &&)

\b -> (&&) a b

(&& b)

\a -> (&&) a b

然而，通过-XPostfixOperators 扩展，左边的部分是η-reduced，所以(a &&) 被解构为(&&) a 。

元组部分也被翻译成lambdas。

Haskell	核心

(,True,)

\a ->
\b ->
  (,,) a True b

多参数模式匹配

对多个参数进行匹配的函数被翻译成嵌套的案例表达式。

Haskell	核心

and True  True  = True
and True  False = False
and False True  = False
and False False = False

and =
  \(a :: Bool) ->
  \(b :: Bool) ->
  case a of
    False ->
      case b of
        False -> False
        True  -> False
    True ->
      case b of
        False -> False
        True  -> True

在Core中用'case'进行匹配并不像在表面Haskell中那样复杂。它将参数强制为WHNF，然后更像 C 中的 'switch' 语句，比较构造器标签。所以要在多个变量上进行匹配，我们需要多个大小写表达式。

深度模式匹配

需要深入查看数据的模式匹配也会解糖为嵌套的大小写表达式：

Haskell	核心

f (Left (Just "")) = True
f (Right ()) = True
f _ = False

f =
  \e ->
    case e of
      Left l ->
        case l of
          Nothing -> False
          Just s ->
            case s of
              [] -> True
              (:) a b -> False
      Right r ->
        case r of
          () -> True

在第一个函数子句中，我们分步检查输入值。我们检查我们被赋予的：

Left 的构造函数Either ，它包含了
Just 的构造函数Maybe ，它包含...
一个空字符串，由内置列表的[] 构造函数表示。

在Core中，我们对每个这样的步骤都有一个案例表达式。

兰姆达案例

-XLambdaCase 的扩展......是非常不言自明的：

Haskell	核心内容

\case
  True -> False
  False -> True

\x ->
case x of
  True -> False
  False -> True

如果-那么-相反

一个if-then-else表达式被翻译成一个简单的case-expression。

哈斯克尔	核心

if c
then a
else b

case c of
  False -> b
  True  -> a

这个翻译非常直接，让人怀疑为什么if-then-else会出现在语言中。但在-XMultiWayIf ，事情就变得更有趣了，我们又开始看到嵌套的案例表达式。

Haskell	核心

if | c1 -> a1
   | c2 -> a2
   | c3 -> a3
   | otherwise -> a4

case c1 of
  False ->
    case c2 of
      False ->
        case c3 of
          False -> a4
          True -> a3
      True -> a2
  True -> a1

`seq` 函数

'seq'函数，强制对其参数进行弱头正常形式的评估，被解构为一个案例表达式，依靠的是Core中案例表达式是严格的：

Haskell	核心

seq a b

case a of
  _ -> b

Bang模式与'seq'几乎是一回事，因为它们也被翻译成了严格的大小写表达式：

Haskell	核心

f, g :: Bool -> Bool
f  x = x
g !x = x

f = \x -> x
g =
  \x ->
  case x of
    _ -> x

这里，f 是身份函数，而g 也将其参数强制为 WHNF。

参数化的多态性

现在，为了更有趣的东西，让我们来谈谈参数化多态性。这就是我们开始看到Core中不容易在Haskell中看到的部分。在Core中，只要你有一个类型参数，它就必须被一个lambda绑定，就像它是一个普通的函数参数一样。

Haskell	核心

id :: forall a. a -> a
id x = x

id =
  \ @(a :: Type) ->
  \  (x :: a) ->
      x

在这里，在id 函数中，我们有一个lambda用于a 类型参数，然后有一个lambda用于x 值参数（类型为a ）。

当我们使用一个多态函数，如id ，在表面Haskell中，我们只需给它提供值参数。但在Core中，我们还必须提供类型参数：

Haskell	核心

t :: Bool
t = id True

t = id @Bool True

这给了我们一个关于-XTypeApplications 扩展的有用视角。事实上，它是Core的一部分在surface Haskell中出现，只不过在Core中，它是强制性的。

再举个例子，当你构造一个有三个元素的元组时，在Core中你会传递六个参数。首先是元素类型，然后是元素：

Haskell	核心

p = (True, 'x', "Hello")

p =
  (,,)
    @Bool
    @Char
    @String
    True
    'x'
    "Hello"

存在性量子化

为什么明确地传递类型参数是一个有价值的想法？其中一个原因是，它揭开了存在性量化的神秘面纱，我个人在这方面纠结了很久。看一下Core就会发现，存在性类型参数的行为就像数据构造器的其他字段：

Haskell	Core

data E =
  forall a. MkE [a]

lenE :: E -> Int
lenE (MkE xs) =
  GHC.List.length xs

lenE =
  \(e :: E) ->
  case e of
    MkE @a xs ->
      GHC.List.length @a xs

当我们在这里对MkE ，在原始程序中只有xs 被带入范围。但是在Core程序中，存在性类型变量也被带入了范围，然后传递给了length 函数。

还有一个保证就是类型信息会在以后的传递中被擦除，所以在运行时没有开销。但在核心层，它的行为真的就像与其他数据一起存储一样。

类和字典传递

在Core中，不存在类型类。类的实例在Core中被明确地传递，作为普通数据。这些值被称为 "字典"，但它们并没有什么特别之处。与类型参数不同，它们是在运行时传递的：

Haskell	核心

f :: Num a => a -> a
f x = x + x

f = \ @(a :: Type) ->
    \ ($dNum :: Num a) ->
    \ (x :: a) ->
      (+) @a $dNum x x

这里，我们有一个Num a 约束，但在Core中，它只是另一个函数参数，我们把它绑定到$dNum 变量上。这个$dNum 值包含了(+) 、(*) 、和其他Num 方法的实现，用于给定的a 的选择。

因此，虽然在表面的Haskell中，看起来f 有一个参数x ，但在解构为Core后，它实际上有三个参数。

a :: Type, 其输入/输出的类型（例如，Int 或Double ）。
$dNum :: Num a, 带有方法实现的类字典
x :: a, 输入值

而当你使用一个带有类约束的多态函数时，你需要将类字典传递给它：

Haskell	核心

f :: Int -> Int
f x = x + x

f =
  \(x :: Int) ->
  (+) @Int $dNumInt x x

这里的$dNumInt 包含所有Num 方法的实现，用于Int 。这是一个由Num Int 实例创建的值。

Haskell	核心

instance Num Int where ...

$dNumInt = ...

正如你所看到的，类的实例被解构为值的绑定。

做记号

让我们看看这一切是如何在do-notation中实现的。每个绑定都对应着对(>>=) 操作符的使用：

Haskell	不完全是核心

f act = do
  x <- act
  y <- act
  return (x && y)

f = \act ->
  act >>= \x ->
  act >>= \y ->
  return (x && y)

但我们知道，Core中没有运算符。另外，(>>=) 是多态的，所以我们需要传递一个类型参数和Monad 实例字典给它。所以实际的Core看起来是这样的：

Haskell	核心

f act = do
  x <- act
  y <- act
  return (x && y)

f =
  \ @(m :: Type -> Type) ->
  \ ($dMonad :: Monad m) ->
  \ (act :: m Bool) ->
    (>>=)  @m $dMonad @Bool @Bool act (\x ->
    (>>=)  @m $dMonad @Bool @Bool act (\y ->
    return @m $dMonad @Bool ((&&) x y)))

首先，我们把m 类型变量作为输入。在f 的使用地点，用户将把m 实例化为类似IO,Maybe,[],Either e,Reader r,Writer w, 等等。
第二个参数是Monad 类型类的字典。它包含了(>>=) 和return 的实现，用于给定的m 的选择。
然后我们有单体动作本身，act 。

该函数的其余部分是人们所期望的：我们调用(>>=) 函数来连锁单体动作，但我们也向它提供了类型参数和Monad 类字典。

虽然单体一开始看起来很神秘，涉及到类型类、参数化多态性，以及上面的do-notation糖，但它们最终只是一堆lambdas和函数应用。

强制执行和转换

Core有两个额外的特性是Haskell所不具备的--强制（coercions）和转换（cast）。这两个功能是紧密联系在一起的：

data Expr
  = Var   Id
  | Lit   Literal
  | App   Expr Expr
  | Lam   Var Expr
  | Let   Bind Expr
  | Case  Expr Var Type [Alt]
  | Cast  Expr Coercion
  | Type  Type
  | Coercion Coercion

在生成的Core中观察它们的一个方法是使用一个平等约束。让我们从身份函数开始，并通过添加一个平等约束来使事情变得更加有趣。

平淡	辣的

id :: a -> a
id x = x

id :: (a ~ b) => a -> b
id x = x

与我们熟悉的身份函数不同，它把a 带到a ，把a 带到b ，但同时它要求证明a 和b 是同一类型。当我们把这个程序翻译成Core时，在那里我们明确地做所有的事情，有两个缺口需要填补。

Haskell	Core

id :: (a ~ b) => a -> b
id x = x

id =
  \ @(a :: Type) ->
  \ @(b :: Type) ->
  \ ???₁ ->
  \ (e :: a) ->
     e ???₂ :: b

当然，我们绑定了类型变量，a 和b ，但是应该有某种绑定的平等约束。这是第一个缺口，这也是强制器发挥作用的地方。

Haskell	核心

id :: (a ~ b) => a -> b
id x = x

id =
  \ @(a :: Type) ->
  \ @(b :: Type) ->
  \ (co :: a ~ b) ->
  \ (e :: a) ->
     e ???₂ :: b

胁迫作为类型平等的证据。如果你有一个类型为a ~ b 的强制器（比如上面的co ），那么你可以将类型为a 的表达式转换为类型为b 的表达式（或者反过来，因为平等是对称的）。

而这正是我们需要做的，以填补第二个缺口。e 值的类型是a ，但是函数必须返回一个类型为b 的值。我们通过在转换中引用它来使用coercion。

Haskell	核心

id :: (a ~ b) => a -> b
id x = x

id =
  \ @(a :: Type) ->
  \ @(b :: Type) ->
  \ (co :: a ~ b) ->
  \ (e :: a) ->
     e |> co

我们把这个转换写成|> ，它的作用是指导Core的类型检查器。与Haskell的类型检查器不同，它不做任何形式的推理或高级推理。明确的强制和转换使得类型检查程序变得简单而直接。

GADTs

关于强制器的一个有趣的事情是，你可以把它们放在数据构造函数中。我们已经看到了在数据构造函数中存储类型变量是如何解释存在性量化的。数据构造函数中的强制器是GADTs的基础。

Haskell	核心

data G a =
  (a ~ Int) => MkG a

f :: G a -> Int
f (MkG n) = n

f = \ @(a :: Type) ->
    \  (g :: G a) ->
  case g of
    MkG co n -> n |> co

这里MkG 也存储了一个证明，即a 等于Int 。因此，当我们在MkG 上进行模式匹配时，在Core中我们得到了一个作为这种平等性证据的强制子。a然后我们可以在转换中使用它：我们有一些未知类型的n ，但我们需要返回一个Int 。协约co :: a ~ Int ，正是我们需要的，以说服类型检查器，这实际上是好的。

当构造一个类型为G a 的值时，我们必须提供这个协约，所以不可能得到一个非分歧类型的表达式，例如G Bool ，因为Haskell的类型检查器不会产生一个类型为Bool ~ Int 的协约。

类型家族

胁迫也被用于解糖类型家族。当你有一个类型实例时，在Core中，它对应于一个公理，由一个coercion表示。

Haskell	核心

type family F a
type instance F Bool = String

fBoolString =
  Axiom :: F Bool ~ String

然后，这个由类型族实例创建的强制器可以被用于转换。

证明语言

协同器构成了GHC的内部证明语言：

iy40hf7u.pasted_image_0.png

但是这种语言的具体细节更多的是技术性的，除非你正在研究形式主义或扩展GHC的类型检查器，否则你不需要它们。

重要的一点是明确地传递平等证明，并在转换中使用它们的想法。

总结

丰富的Haskell特性可以简化为GHC核心的少数特性。执行这种转换的编译器传递被称为脱ugaring，它发生在解析、名称解析和类型检查之后。

思考Haskell语言结构在Core中被解构的方式，可以更深入地理解这些特性，而不是肤浅的熟悉。例如，它为存在性量化、GADTs和do-notation提供了清晰的直觉。

在日常编程中，当你调查某段代码的性能时，阅读编译器生成的Core可能会很有用。如果你打算为GHC做贡献或者写一份提案，Core也是一项有价值的知识。

Haskell to Core:通过解构了解Haskell的特性