如何实现LR(1)解析器

迟早有一天，你会尝试给自己写一门编程语言。而其中的第一部分很可能是一个解析器。

有两组主要的解析方法：

1. 递归血统。LL（包括解析器组合器/packrat），PEG。
2. 递归上升法。LALR(1), LR(1), 等等。

递归的方法是比较容易的，但它们也有问题：

1. 没有左侧递归：如果你的语法有非显著的左递归部分，你会花很多时间来重新安排它们。
2. 没有冲突解决：如果你的两个冲突规则能够解析相同的输入，那么left / right 中左边的那个将获胜（其中/ 是一个偏左的选择运算符）。简而言之，它将隐含地选择哪一方获胜。
3. 回溯：它们不仅会导致同一文本被解析两次，而且如果你的解析库/生成器没有默认禁用回溯--就像parsec 库通过给你提供try 组合器来有选择地打开它--你可能会对某些输入文本产生指数级的解析时间。
4. 时间复杂度：使一个解析器在时间限制上呈指数级，实际上比你想象的要容易。

上升的方法：

0. 有一个由Knuth编写的一般实现的算法。
1. 接受左和右递归。
2. LR(1)发现 冲突并显示它们。
3. 绝不回溯。
4. 保证线性时间的工作。

(这是我的观点，因为我一直在使用解析器组合器形式的LL，所以有偏见。下降法也有其优点。你可以自由地使用你喜欢的任何解析方法！)

LR的问题在于它显得复杂而神秘，如果你打开Knuth的原始论文--你几乎会立即说 "不对！"。

在这篇文章中，我将试图解释LR(1)表解析算法，这样你就可以自己遵循并实现它，而不局限于使用像yacc 、menhir 或happy 这样的生成器。

我还认为，所有重要算法的实现都应该在人代中重写一次，这样工具链就不会变得无法使用，代码也能保持适应当前标准。

语法

现在每个严肃的分析器都从某种形式的语法开始--如yacc 、Menhir 、ANTLR 或happy 。

我将使用稍加修改的Backus-Naur形式（或BNF）来表示语法。

我们的算法将假定已经运行了一个词法分析器，并产生了一个标记的标记流供我们使用。

让我们来描述大家都知道的经典语法：算术。

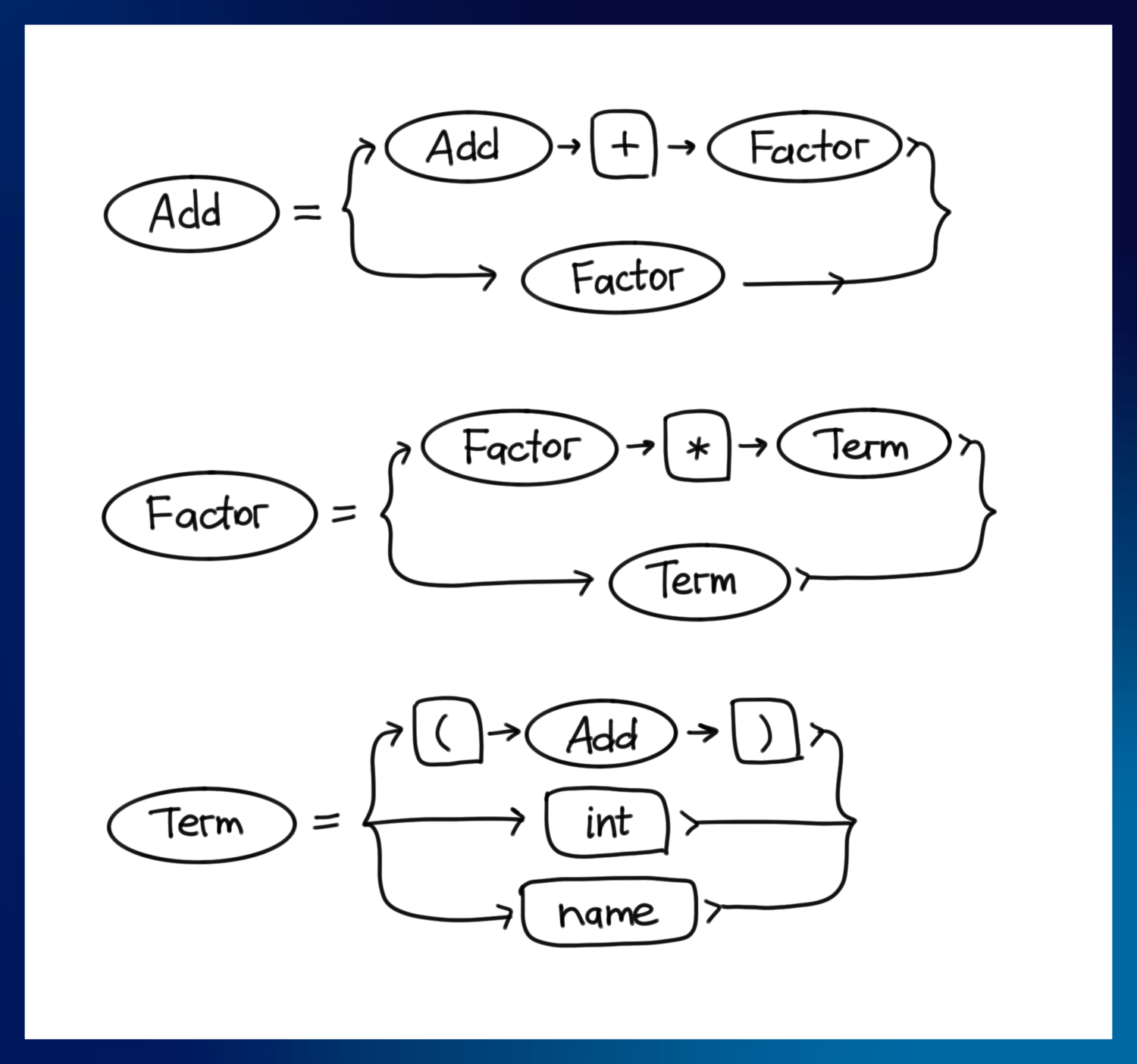
我将使用以下惯例：

1. 大写的单词--Add,Factor,Term 是非终结词，或结构。
2. 小字词 -name,int 是终端，其定义被省略。
3. 双引号的词 -"(","+" 是有固定形状的终端。
4. -> 右边的代码是一个语义动作，当规则被解析到最后时，它被用来从规则组件中构建AST节点。我们只需要它们一次，所以为了清晰起见，在这之前我将省略它们。

这就是我们的语法：

Start  = Add              -> id
Add    = Add "+" Factor   -> mkPlus
       | Factor           -> id
Factor = Factor "*" Term  -> mkMult
       | Term             -> id
Term   = "(" Add ")"      -> nth 1
       | name             -> mkName
       | int              -> mkInt

我将不允许在规则根之外使用Kleene star (*), Kleene plus (+), optionality operator (?), 和choice operator (|) 。包含它们的语法几乎可以机械地还原为这种 "正常形式"。

我将不允许任何规则匹配空字符串，并假设没有规则匹配。这将使算法的某些部分更容易制作。

我还将使用这种语法的一个稍微不同的形式：

Start  = Add

Add    = Add "+" Factor
Add    = Factor

Factor = Factor "*" Term
Factor = Term

Term   = "(" Add ")"
Term   = name
Term   = int

这种形式完全删除了| 算子，同时保留了该语法的语义。

我将把一个点称为任何单数终端或非终端。

我还将交替使用地图和函数这两个术语。大多数编程语言都提供了将一个变成另一个的方法（记忆化）。

关于算法的一些见解

推倒

我们将制作一个推倒式自动机--这意味着我们将有一个或两个堆栈，在那里我们将收集部分树并对它们运行语义行动。在某种意义上，堆栈可以被看作是深度优先遍历的一种状态*，其结果是树的脊柱*。

例如，我们可以有一个堆栈。

Factor : "+" : Add : ...rest

而当下一个输入是"*" ，我们也推送它。

在其他的输入中，我们可能会选择从堆栈中弹出Factor,"*", 和Add ，对它们调用mkPlus ，然后再把结果推回，最后堆栈的样子是这样的：

Add : ...rest

非终端的概念

我喜欢将非终端视为其可能的实现的集合（或类）--或可匹配的终端序列。例如，a * 42 是Factor 集的成员，因为它可以用Factor 作为起始非终端进行解析。

除此之外，非终端可以被看作是在文本中插入括号的方式：b + a * 42 ->b + [a * 42] -- 这里我们把a * 42 识别为Factor 。

我想让读者注意的是，非终结符不会给它们分组的文本部分增加任何东西。它们是完全透明的，所以你可以用它们的主体来替换语法中对它们中任何一个的引用，而这不会改变任何东西。只要记住，应该插入带有所有替代物的整个主体（结果需要再次转换为正常形式）。

本段的意图是，在进一步阅读时，它可能会让你 "点击"。

传递性封闭

在我们进一步行动之前，我们需要讨论一种机制，它将使几乎所有部分的实现都接近于微不足道。

一个函数的传递性闭合是它的固定点，它在被应用于种子足够多的次数后会达到这个固定点。

更正式地说，某个函数f （在某个种子x ）的传递性闭合是一个表达式f (f (f (... (f x) ...))) 。当然，这个表达式将是无限的。

做一个实际的传递性闭包的最简单的方法是将f 应用于某个累积器x ，直到它停止变化。

如果说，f 在两次调用后停止变化，那么f (f x) 与f (f (f x)) 相同。通过归纳，它将与f (f (f (... (f x) ...))) 相同。这意味着，当我们注意到最后一次调用没有增加任何新内容时，我们可以省略 "无限期应用 "的部分。

让我们看看一个实际的例子：对于每个非终端，我们将寻找一组可以紧随其后的终端。

我们的语法，供参考：

Start  = Add             -- can be followed by $

Add    = Add "+" Factor  -- Add can be followed by "+"
Add    = Factor

Factor = Factor "*" Term -- Factor can be followed by "*"
Factor = Term

Term   = "(" Add ")"     -- Add can be followed by ")"
Term   = name
Term   = int

我们的accumulator :: NonTerm -> Set<Term> 是{Start: {$}}

对于每个规则组，我们进行以下制作。

{ Start:  {$}
, Add:    {"+", ")", $}
, Factor: {"*"}
, Term:   {}
}

地图已经改变，所以我们用它作为新的累加器重新开始。

现在我们得到以下结果：

{ Start:  {$}
, Add:    {"+", ")", $}
, Factor: {"*", "+", ")", $} -- because Add ends with Factor
, Term:   {}
}

在接下来的迭代中，我们得到：

{ Start:  {$}
, Add:    {"+", ")", $}
, Factor: {"*", "+", ")", $}
, Term:   {"*", "+", ")", $} -- Factor ends with term
}

接下来的迭代将不会改变累加器，因此我们已经达到了初始点。

$ 正如你所看到的，尽管该算法最初不知道Term ，但它还是设法将信息传播到各处，尽管如此。

当然，并不是每个函数都会像f 那样做得很好，并能收敛。但我们为这篇文章编写的所有函数都会。

这个函数将自动解决很多问题以后我们会需要一些递归依赖的关系，就像作为例子的那个关系--如果你有这个递归闭包，你就不必担心你计算的顺序。比如，根本不用。如果你为它提供一个传播的步骤，那么这个递归闭包将为你传播结果。

我们将在转换（或者说，"填充"）集合和映射的函数上使用传递性闭包。对于有Haskell背景的读者，我推荐使用一个叫monoidal-containers 的包中的映射。

我还将假设你使用不可变的地图和集合。

插件和适配器

当然，我们的transClosure 与做Set<A> -> Set<A> 或Map<K, Set<V>> -> Map<K, Set<V>> 转换的函数一起工作。但是，例如，函数entails :: Position -> Set<Position> 并不属于这些类别中的任何一个。在这种情况下，由于我们必须提出一个类型为Set<Position> -> Set<Position> 的函数，我们只需在整个输入集合上应用entails ，并将集合的集合平移为一个集合（在Haskell中，我们只需做transClosure (foldMap entails)) ）。

Set<A> -> Set<A> 类型中的第一个Set<A> 是 "到此为止我们拥有的知识 "或 "到此为止我们拥有的新知识"。后者的实现有点麻烦，但最后的结果是一样的。

我们稍后将与集合的映射和集合的映射一起工作，同样需要计算某个函数的反式闭合。在这种情况下，合并地图时应该特别注意：如果地图m1 和m2 都包含相同的键a ，那么得到的地图应该包含a: m1[a] <> m2[a] ，其中<> 是合并操作，m1[a] 是索引。这也适用于Haskell，除非使用monoidal-containers 。在这种情况下，Monoid 实例将为你做这件事。

而适配器也将是，foldMap ：我们将地图中的所有值集合并成一个输入集，将函数映射到它上面，然后按照上面的描述进行深度合并。

第一张表

我们还需要2个辅助表：FIRST 和FOLLOW 。这里我们将建立FIRST 。

该函数的类型为FIRST :: NonTerminal -> Set<Terminal> ，对于语法中的每个非终端，它将返回所有可以开始的终端。

对于每个规则，我们将分析它的第一个点：

1. R = . a ...rest - 在这种情况下，我们在我们的知识中添加 。{R: {a}}
2. R = . A ...rest - 在这种情况下，我们添加 。{R: FIRST(A)}

当然，也可以有这样的规则：

R = A ... | ...
A = R ... | ...

但这并不妨碍我们的工作!我们将使用传递性闭包来克服这个问题。

我们还将使用一个空集作为我们封闭的种子。

这个操作的一步很简单：我们扫过所有的规则，并以上述方式对其第一项作出反应。然后，我们将所有的地图深度合并成一个，这将被封闭机制添加到知识中。

跟随表

这件事有点棘手。对于每个非终端，我们需要根据语法构建一个可以紧跟该非终端的终端集。

该算法的这一部分也使用FIRST 表来构建。

因此，对于语法中每个规则的每个位置，我们将查看其位置和该规则的下一个位置的位置：

1. ... = ... . R a - 在这种情况下，我们将 加入我们的知识。{R : {a}}
2. ... = ... . R A - 这里我们添加 。{R : FIRST(A)}
3. A = ... . R - 这里的 ，后面可以跟上 ，因此 。R A {R : FOLLOW(A)}
4. ... = ... R . - 在这种情况下，不能添加任何信息。

同样，我们使用了与FIRST 相同的方式来使用传递性闭包。我们合并上面的扫描结果，用一个空地图作为起始种子。

位置

位置在文献中也被称为LR(1)-item。

在解析的不同阶段，解析设备会翻阅表格，在规则内部从左到右移动。我们需要一种方法来表示这种移动。为此，我们将添加一个新的实体：解析位置（或只是位置）。

例如，规则Add = Add "+" Factor ，有4个位置：

Add = . Add "+" Factor
Add = Add . "+" Factor
Add = Add "+" . Factor
Add = Add "+" Factor .

光标 . ，描述了解析设备所站的位置。左边的一切都被假定为被解析了，右边的一切都将被解析。我们将把光标之后的直接点称为位置。

然而，位置本身并不足以建立一个解析器表。例如，让我们拿Add = Add "+" . Factor 。

如果堆栈的最上面的元素是Factor ，我们可以在它上面移动到Add = Add "+" Factor . 。如果最上面的元素是Term ，这意味着当我们还在Add = Add "+" . Factor 的位置时，我们也在解析Factor = . Term 的位置。

可以说，Add = Add "+" . Factor 的位置也包含了Factor = . Term 的位置--而且，过渡性地包含了Term = . name 的位置，但反之亦然。

这是因为在Add = Add "+" . Factor ，我们可以把name 、int 和"(" 作为有效的输入，我们必须能够以某种方式处理这个问题。

如果C 是一个非终端，我们说位置A = B . C 包含了C 的所有初始位置。位置A = B C . 或A = B . c 不包含任何东西，因为它们的位置相应地是什么也不是或一个终端。

该位置还应该存储一组可以跟随其完全解析版本的终端。

解析器的状态将是这种包含关系的反式闭合。

解析状态

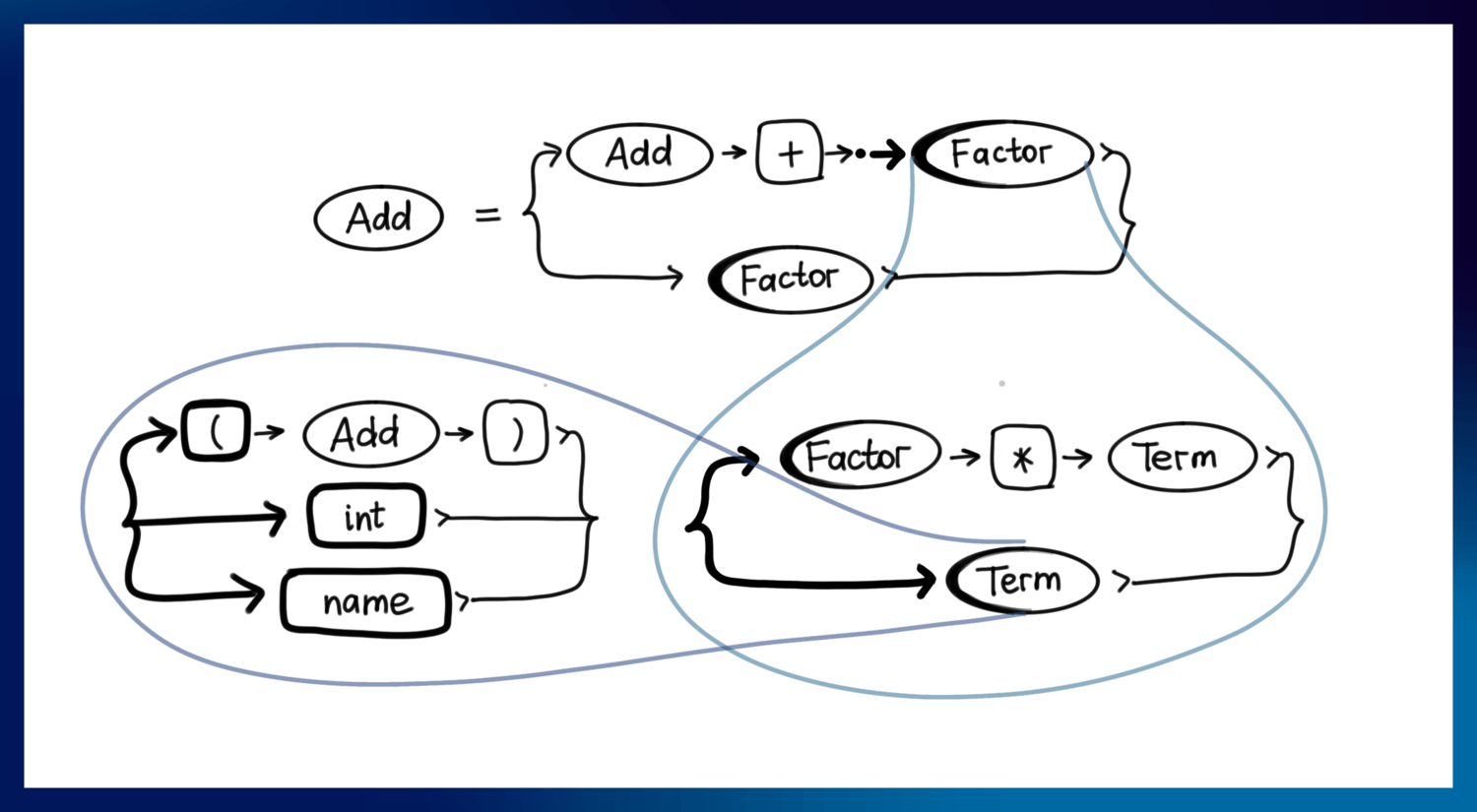
我们使用我们开始的位置作为转义闭包的种子。

我们将把 "反式闭合的entailment "称为CLOSURE ，字体为大写字母和单空格。我们将把CLOSURE 定义为。

CLOSURE :: Position -> State

和：

type State = Set<Position>

该算法如下。

对于起始集合中的每个位置，如果其位置包含一个终端或为空，则不向状态中添加新的位置。如果它是一个非终端，那么该终端的所有起始位置都被添加到集合中，它们的lookahead集合被改变为FIRST(Next) ，其中Next 是在该位置中跟随定位的点。如果没有任何东西跟随定位点，那么lookahead集合就变成了FOLLOW(Entity) ，其中Entity 是规则的输出非终端。

如果该状态最终有几个具有相同主体但不同lookaheads的位置，它们应该被合并为一个。

对于一个例子，我们将采取不同的语法，其中lookahead变化的影响更加明显：

S = a A b
S = a B d
S = c A d
S = c B b
A = x
B = x

我们的起始集将是：

{ S = a . A b {$}
, S = a . B d {$}
}

例如，必然性的一个步骤是这样的：

{ S = a . A b {$}
, S = a . B d {$}
, A = . x     {b}
, B = . x     {d}
}

A 规则现在有一个lookahead集，即{b} ，因为b 在规则S = a . A b {$} 中跟随。同样的逻辑导致B ，得到了一个lookahead集，即d 。

源规则本身保留了它们开始时的前瞻集。这适用于所有对必然性的传递性调用。

这就是LR(1)与SLR的区别，也是LR(1)表大小增加的原因。

我还应该指出，解析设备同时存在于所有这些位置。

GOTO表

是的，"goto 被认为是有害的"--如果有人还记得这是什么意思。但我们正在制作一个不同的GOTO 。

我们的GOTO 是一个表格，对于每个状态和可能的堆栈顶部元素，告诉我们下一步应该去什么状态（在某些情况下）。

我们将再次写出如何计算转化的1步，而转义闭包将为我们做剩下的事情。

我们的一步goesTo :: State -> Map<State, Map<Point, State>> 函数应该做以下事情。

对于输入状态中的每一个具有非空定位的位置，这个定位的内容应该导致这个位置的CLOSURE ，进阶--查询集改为FIRST(NextNonTerminal) 或下一个终端。

例如，让我们在这个规则里面取一个任意的位置：

Add = Add "+" Factor {"+", ")", $}

比如说这个：

{ Add    = Add "+" . Factor  {"+", ")", $}
, Factor = . Factor "*" Term {"*", "+", ")", $}
, Factor = . Term            {"*", "+", ")", $}
, Term   = . "(" Add ")"     {"*", "+", ")", $}
, Term   = . name            {"*", "+", ")", $}
, Term   = . int             {"*", "+", ")", $}
}

与

"("

引发的情况

Term = "(" . Add ")" {"*", "+", ")", $}

导致的状态

CLOSURE(Term = "(" . Add ")", {"*", "+", ")", $})

包含，除其他外，以下位置：

{ Add = . Add "+" Factor {")"}
, Add = . Func           {")"}
}

注意，在查找集合中只有")" - 在这种状态下，不可能有其他东西导致减少

和与

Factor

导致

CLOSURE(Factor = Factor . "*" Term)

而GOTO 函数是对goesTo 的一个传递性闭合，其中有足够的foldMap-s。以{ Start = . Whatever {$} } 作为初始状态--这就是为什么我们首先要有这个规则。

这个函数将终止于无处可去的最终位置（如Add = Add "+" Factor . ）。

但是我们仍然不能只用GOTO 来进行解析。你可能听说过，LR(1) 是与shift 或reduce 等词一起使用的--你是对的。我们现在将更接近这部分。

GOTO :: Map<State, Map<Point, State>> 的顶部键集也将作为所有可能的非最终状态的集合，我们将在下一个区块中运用它。

ACTION表

GOTO 是好的，但是我们没有点作为输入--我们有终端。所以我们需要有一些 关系。我们也将为此使用 函数。(State, Terminal) -> Decision GOTO

Decision 是2的一个（实际上是3到5）：

• Shift (state1) - 把当前的终端推到堆栈上，然后转到 。state1
• Reduce (R = A b C . {a b c} -> mkR) - 从堆栈中弹出一些东西，在它上面调用一个 动作，将结果推入堆栈，并返回到状态 。mkR GOTO(current, R)
• Error - 死得很惨，告诉大家在那个位置应该有什么终端。
• Accept - 只有在 ，当下一个终端是输入结束的终端（ ）时才会使用。达到它意味着我们已经完成了。Start = Whatever .``$
• Conflict (dec1, dec2) - 我们将用这个决定来表示，对于这个语法来说，一组冲突的结果是可能的。它使我们能够用 "对于这个语法，你有48个移位/减法和4个减法/减法冲突 "的信息来取悦用户。

所以，让我们回到我们心爱的例子状态：

{ Add    = Add "+" . Factor   {"+", ")", $}
, Factor = . Factor "*" Term  {"*", "+", ")", $}
, Factor = . Term             {"*", "+", ")", $}
, Term   = . "(" Add ")"      {"*", "+", ")", $}
, Term   = . name             {"*", "+", ")", $}
, Term   = . int              {"*", "+", ")", $}
}

我们需要搜索两类东西：

1. 像Term = . name {...} 这样的位置，期望有一个终端。
2. 像Factor = Factor "*" Term . {...lookahead} 这样的位置，是最终的位置。

第一组位置将产生Shift-s。例如，"(" 终端将产生以下关于当前状态的地图：

{ currentState =>
  { "(" =>
    Shift (CLOSURE (Term = "(" . Add ")"))
  }
}

第二组位置将产生Reduce-s。对于每个终端（例如，"+"）是在该位置的规则的lookahead集合中，我们产生：

{ currentState =>
  { "+" =>
    Reduce (Factor = Factor "*" Term . { mkR } -> mkMult)
  }
}

我们对GOTO 表的每一个状态都这样做，然后将所有的结果合并成一个地图。

冲突

我们可能会在这样的情况下结束：对于同一个状态和输入终端，可能有两个决定是不同的，而其中没有一个是Error 。

在这种情况下，我建议把这个单元格标记为Conflict (one, another) ，然后继续深入。稍后，当表格完成后，我们可以扫过它，将所有的冲突呈现给用户，如果有的话。

错误报告

当你的分析器说：Syntax error. ，这不是很有趣。我们可以做得更好。

我们首先需要的是我们语法中所有终端的集合。

对于第二部分，我们需要遍历ACTION 表，收集所有不导致空单元或Error 的(state, input) 对。从这些中，我们构建一个从状态到它们期望的输入的地图。我们将该地图称为EXPECTED 。

我们将在解析器设备中使用该地图。

剖析器

现在我们有了构建解析器的所有机制。

它的状态应该有两个堆栈：一个是部分程序树（值堆栈），另一个是解析器的状态（控制堆栈）。初始状态是CLOSURE(Start = Whatever . [$]) 。

解析器还应该能够逐一读取输入流，并且应该具有对下一个未被吸收的输入的读取权限。

有一件微妙的事情：解析器接受的是输入流，而不是终端--后者是输入的类别（42 是一个输入，int 是一个终端）。词典（这不在本文的讨论范围之内）应该把这些类分配给输入，或者产生一个(input, terminal) 对的流。

解析循环如下：

1. 读取下一个token 。
2. 取最上面的状态和(1)中的标记，查找ACTION(state, token) 。
   1. 在Shift (state2) ，将token 和state2 推入相应的堆栈，并从输入流中删除标记。
   2. 在Accept ，退出循环并返回值栈的顶部元素作为解析结果。
   3. 在Reduce (R = ...rule -> action) 。
      1. 从两个堆栈中弹出N 项目，其中N 是一个规则的长度，单位是点。
      2. 处理从控制栈中弹出的元素。
      3. 将规则的语义action ，应用于值栈中被弹出的元素。
      4. 将(3)的结果推入值栈，将GOTO(currentState, R) 的结果推入控制栈。
   4. 在Expected - 产生一个错误信息，使用EXPECTED(state) 集。
3. 转到(1)。

结论

这里仍然有很多东西可以优化。例如，你可以把状态塞进一个数组，使用它们的索引而不是直接使用状态（这将导致你在地图中对一个集合进行查找）。

你可以把表的计算移到编译时，把表嵌入到程序中。需要注意的是，LR(1)的表通常非常大，所以建议使用地图而不是非稀疏数组。

你可以通过从动作表中收集更多的数据来增强错误报告--或者通过解释解析器堆栈的N 元素。

你还可以给规则添加优先级，这样当它们最终对同一状态和终端产生不同的动作时，就可以避免冲突（或者说，默默地解决）。

有了这些，LR(1)的一个基本实现就完成了。它将接受左和右递归语法，自动检测冲突，并对O(N) ，其中N 是输入的长度，进行无回溯的文本解析。