C++笔记day23 单向链表 受限线性表：队列 二叉树 插入排序

吞吴
99 阅读9分钟

队列  Queue

符合 先进先出的数据结构

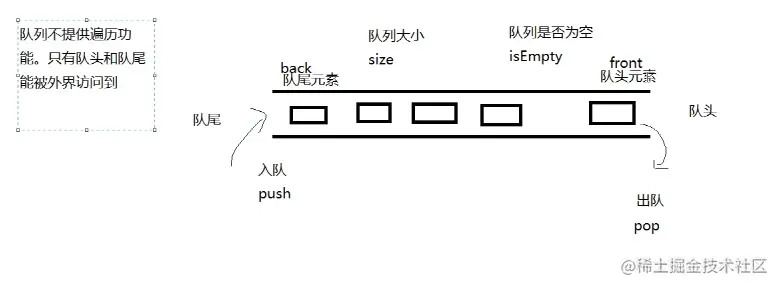
image.png

术语：

入队  push

出队  pop

返回队列大小  size

判断是否为空  isEmpty

队头元素  front

队尾元素  back

队列的顺序存储

利用数组模拟出 先进先出的数据结构

接口：

初始化队列  init

入队  push

出队  pop

返回队列大小  size

判断是否为空  isEmpty

队头元素  front

队尾元素  back

销毁队列  destroy

示例

#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>
#include "SeqQueue.h"
#include "DynamicArray.h"

//初始化队列
seqQueue initSeqQueue() 
{
	struct dynamicArray * arr = initDynamicArray(MAX);

	return arr;
}
//入队
void pushSeqQueue(seqQueue queue, void* data) 
{
	//本质 尾插
	if (queue == NULL) 
	{
		return;
	}
	if (data == NULL) 
	{
		return;
	}
	struct dynamicArray* myQueue = queue;
	if (myQueue->mSize == MAX) 
	{
		return;
	}
	insertDynamicArray(myQueue, myQueue->mSize, data);
}
//出队
void popSeqQueue(seqQueue queue) 
{
	//本质 头删
	if (queue == NULL) 
	{
		return;
	}
	struct dynamicArray* myQueue = queue;
	if (myQueue->mSize <= 0) 
	{
		return;
	}
	removeByPosDynamicArray(myQueue, 0);
}
//返回队列大小
int sizeSeqQueue(seqQueue queue) 
{
	if (queue == NULL) 
	{
		return -1;
	}
	struct dynamicArray* myQueue = queue;
	return myQueue->mSize;
}
//判断队列是否为空
int isEmptySeqQueue(seqQueue queue) 
{
	if (queue == NULL) 
	{
		return -1;
	}
	struct dynamicArray* myQueue = queue;
	if (myQueue->mSize ==0) 
	{
		return 1;
	}
	return 0;

}
//返回队头元素
void* frontSeqQueue(seqQueue queue) 
{
	if (queue == NULL) 
	{
		return NULL;
	}
	struct dynamicArray* myQueue = queue;

	return myQueue->pAddr[0];
}
//返回队尾元素
void* backSeqQueue(seqQueue queue) 
{
	if (queue == NULL)
	{
		return NULL;
	}
	struct dynamicArray* myQueue = queue;

	return myQueue->pAddr[myQueue->mSize-1];
}
//销毁队列
void destroySeqQueue(seqQueue queue) 
{
	if (queue == NULL)
	{
		return;
	}
	destroyDynamicArray(queue);
}

队列的链式存储

利用链表模拟出 先进先出数据结构

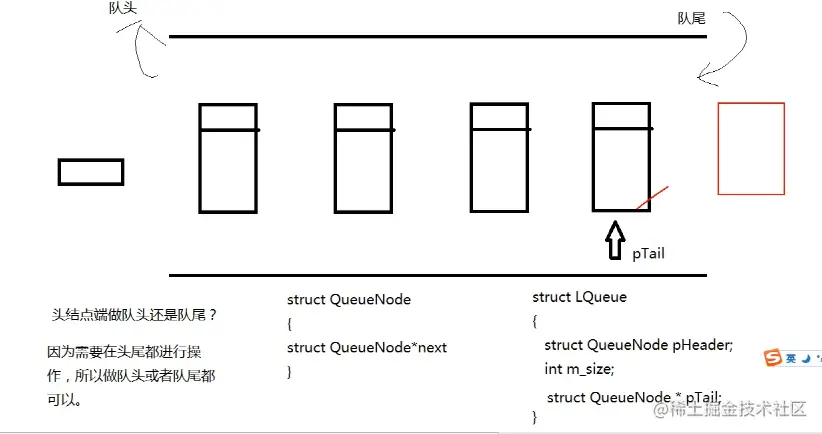
image.png

设计：

节点  只维护指针域

队列结构体：

    struct QueueNode pHeader; 头节点
    int m_Size;  队列大小
    struct QueueNode * pTail; 尾节点指针

接口：

初始化队列  init

入队  push

出队  pop

返回队列大小  size

判断是否为空  isEmpty

队头元素  front

队尾元素  back

销毁队列  destroy

示例

#include "LinkQueue.h"

//初始化队列
LinkQueue initLinkQueue() 
{
	struct LQueue* myQueue = malloc(sizeof(struct LQueue));

	if (myQueue == NULL)
	{
		return NULL;
	}

	myQueue->pHeader.next = NULL;
	myQueue->mSize = 0;
	myQueue->pTail = &myQueue->pHeader;
	return myQueue;
}
// 入队
void pushLinkQueue(LinkQueue queue, void* data) 
{
	if (queue == NULL) 
	{
		return;
	}
	if (data == NULL) 
	{
		return;
	}
	//本质 尾插
	struct LQueue* myQueue = queue;

	struct QueueNode* myNode = data;

	//更改指针的指向
	myQueue->pTail->next = myNode;
	myNode->next = NULL;

	//更新新的尾节点
	myQueue->pTail = myNode;

	myQueue->mSize++;
}
// 出队
void popLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return;
	}

	//本质 头删
	struct LQueue* myQueue = queue;

	if (myQueue->mSize == 0) 
	{
		return;
	}

	if (myQueue->mSize == 1) 
	{
		myQueue->pHeader.next = NULL;
		myQueue->pTail = &myQueue->pHeader; //只有1个节点的时候，要将尾节点还原到头
		myQueue->mSize--;
		return;
	}
	//记录第一个有数据的节点
	struct QueueNode* pFirst = myQueue->pHeader.next;

	//更改指针指向
	myQueue->pHeader.next = pFirst->next;

	//更改链表长度
	myQueue->mSize--;
}
// 返回队列大小
int sizeLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return -1;
	}
	struct LQueue* myQueue = queue;

	return myQueue->mSize;
}
// 判断是否为空
int isEmptyLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return -1;
	}
	struct LQueue* myQueue = queue;

	if (myQueue->mSize == 0) 
	{
		return 1;
	}
	return 0;
}
// 返回队头
void* frontLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return NULL;
	}
	struct LQueue* myQueue = queue;

	return myQueue->pHeader.next;
}
// 返回队尾
void* backLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return NULL;
	}
	struct LQueue* myQueue = queue;

	return myQueue->pTail;

}
// 销毁队列
void destroyLinkQueue(LinkQueue queue) 
{
	if (queue == NULL)
	{
		return;
	}
	free(queue);
	queue = NULL;
}

树的基本概念

由一个或多个(n≥0)结点组成的有限集合T
有且仅有一个结点称为根（root），当n>1时，其余的结点分为**m(m≥0)个互不相交的有限集合**T1,T2，…，Tm。
每个集合本身又是棵树，被称作这个根的子树 。

特点：
    非线性结构，有一个直接前驱，但可能有多个直接后继
    定义具有递归性，树中还有树
    树可以为空，即结点个数为0

术语

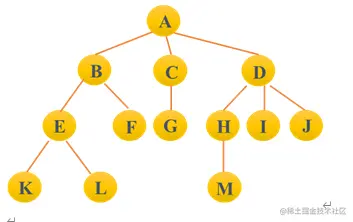
image.png

*根 
    即根结点，没有前驱
*叶子 
    终端结点，没有后继
森林
    m棵不相交的树的集合
有序树
    结点各子树从左至右有序，不能互换（左为第一）
无序树
    结点各子树可互换位置
*双亲  
    即上层的那个结点(直接前驱) parent
*孩子
    即下层结点的子树 (直接后继) child
兄弟
    同一双亲下的同层结点（孩子之间互称兄弟）sibling
堂兄弟
    即双亲位于同一层的结点（但并非同一双亲）cousin
祖先
    即从根到该结点所经分支的所有结点
子孙
    即该结点下层子树中的任一结点
结点
    即树的数据元素
* 结点的度    
    直接后继的数量
结点的层次
    从根到该结点的层数（根结点算第一层）
终端结点
    即度为0的结点，即叶子
分支结点
    除树根以外的结点（也称为内部结点）
*树的度
    所有结点度中的最大值（Max{各结点的度}）
*树的深度(或高度)
    指所有结点中最大的层数（Max{各结点的层次}）

表示法：

图形、广义 、左孩子右兄弟（将多叉树转为二叉树）

左孩子右兄弟表示法 示意图

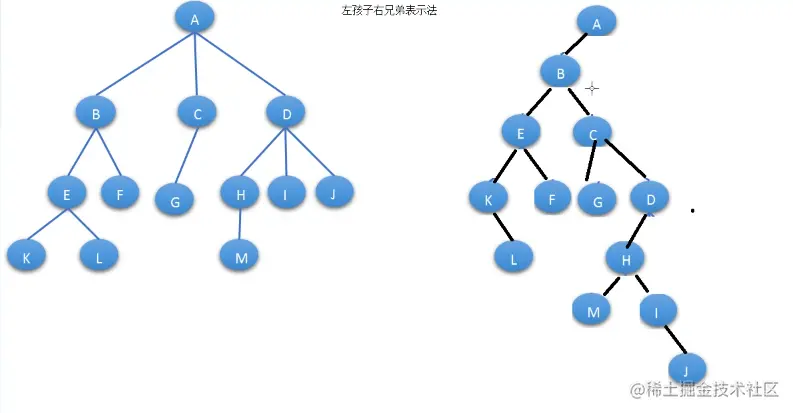
image.png

二叉树的基本性质

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）

性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）

性质3: 对于任何一棵二叉树，若度为2的结点数有n2个，则叶子数（n0）必定为n2＋1 （即n0=n2+1）    度为2 数 + 1 = 叶子数


满二叉树     深度为k的数 并且节点数量为 2^k - 1
完全二叉树   除了最后一层，上面是一颗满二叉树，在最后一层上只缺少右边的若干结点

性质4: 具有n个结点的完全二叉树的深度必为log2n+1 
    (如 log2 (15)    点击 15  log  /  2  log =)

性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

二叉树的递归遍历

先序遍历 ：  先根  再左  再右

中序遍历 ：  先左  再根  再右

后序遍历 ：  先左  再右  再根

image.png

示例

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>

struct BinaryNode 
{
	//数据域
	char ch;
	//指针域
	struct BinaryNode* lChild;
	struct BinaryNode* rChild;
};

void recursion(struct BinaryNode* root) 
{
	if (root == NULL) 
	{
		return;
	}

	//先序遍历
	printf("%c ", root->ch);
	recursion(root->lChild);
	recursion(root->rChild);
	//中序遍历
	recursion(root->lChild);
	printf("%c ", root->ch);
	recursion(root->rChild);
	//后序遍历
	recursion(root->lChild);
	recursion(root->rChild);
	printf("%c ", root->ch);
}

void test01()
{
	struct BinaryNode nodeA = { 'A',NULL,NULL};
	struct BinaryNode nodeB = { 'B',NULL,NULL };
	struct BinaryNode nodeC = { 'C',NULL,NULL };
	struct BinaryNode nodeD = { 'D',NULL,NULL };
	struct BinaryNode nodeE = { 'E',NULL,NULL };
	struct BinaryNode nodeF = { 'F',NULL,NULL };
	struct BinaryNode nodeG = { 'G',NULL,NULL };
	struct BinaryNode nodeH = { 'H',NULL,NULL };

	//建立关系
	nodeA.lChild = &nodeB;
	nodeA.rChild = &nodeF;

	nodeB.rChild = &nodeC;

	nodeC.lChild = &nodeD;
	nodeC.rChild = &nodeE;

	nodeF.rChild = &nodeG;

	nodeG.lChild = &nodeH;

	//递归遍历
	recursion(&nodeA);

}

int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

二叉树编程

求二叉树叶子数量

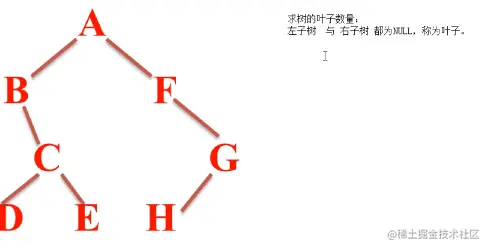
image.png

左子树与右子树都同时为NULL，称为叶子

求二叉树高度

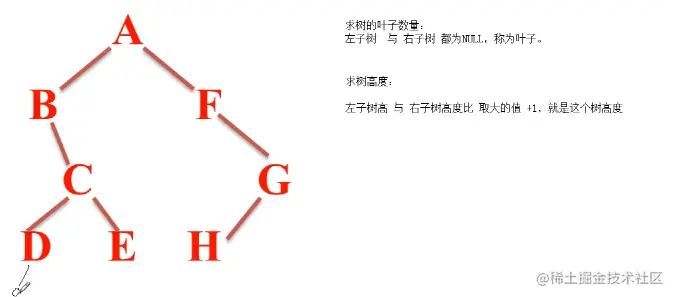
image.png

左子树高度 与 右子树高度比 ，取大的值 +1  就是这个树的高度

拷贝二叉树

先拷贝左子树

再拷贝右子树

再创建根节点  挂载拷贝出的左右子树，返回给用户

释放二叉树

利用递归特性释放二叉树

示例

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>

struct BinaryNode
{
	//数据域
	char ch;
	//指针域
	struct BinaryNode* lChild;
	struct BinaryNode* rChild;
};

//获取叶子数量
void calLeafNum(struct BinaryNode* root, int* p) 
{
	if (root == NULL) 
	{
		return;
	}
	//如果节点 左子树与右子树同时为空，称为叶子
	if (root->lChild == NULL && root->rChild == NULL) 
	{
		(* p)++;
	}
	calLeafNum(root->lChild, p);
	calLeafNum(root->rChild, p);
}

//获取树的高度
int getTreeHeight(struct BinaryNode* root) 
{
	if (root == NULL) 
	{
		return 0;
	}
	//获取左子树高度
	int lHeight = getTreeHeight(root->lChild);
	//获取右子树高度
	int rHeight = getTreeHeight(root->rChild);
	//从左子树和右子树高度选择大的然后+1
	int height = lHeight > rHeight ? lHeight + 1 : rHeight + 1;
	
	return height;
}

struct BinaryNode* copyTree(struct BinaryNode* root) 
{
	if (root == NULL) 
	{
		return NULL;
	}

	//先拷贝左子树
	struct BinaryNode* lChild = copyTree(root->lChild);
	//再拷贝右子树
	struct BinaryNode* rChild = copyTree(root->rChild);

	//创建新的根节点
	struct BinaryNode* newNode = malloc(sizeof(struct BinaryNode));
	newNode->ch = root->ch;

	newNode->lChild = lChild;
	newNode->rChild = rChild;

	return newNode;
}

void recursion(struct BinaryNode* root) 
{
	if (root == NULL) 
	{
		return;
	}
	printf("%c ", root->ch);
	recursion(root->lChild);
	recursion(root->rChild);
}

void freeTree(struct BinaryNode* root) 
{
	if (root == NULL) 
	{
		return;
	}
	//先释放左子树，再释放右子树
	freeTree(root->lChild);
	freeTree(root->rChild);
	//释放根节点
	free(root);
	root = NULL;
}

void test01() 
{
	struct BinaryNode nodeA = { 'A',NULL,NULL };
	struct BinaryNode nodeB = { 'B',NULL,NULL };
	struct BinaryNode nodeC = { 'C',NULL,NULL };
	struct BinaryNode nodeD = { 'D',NULL,NULL };
	struct BinaryNode nodeE = { 'E',NULL,NULL };
	struct BinaryNode nodeF = { 'F',NULL,NULL };
	struct BinaryNode nodeG = { 'G',NULL,NULL };
	struct BinaryNode nodeH = { 'H',NULL,NULL };

	//建立关系
	nodeA.lChild = &nodeB;
	nodeA.rChild = &nodeF;

	nodeB.rChild = &nodeC;

	nodeC.lChild = &nodeD;
	nodeC.rChild = &nodeE;

	nodeF.rChild = &nodeG;

	nodeG.lChild = &nodeH;

	//1. 求二叉树 叶子数量
	int num = 0;
	calLeafNum(&nodeA, &num);

	printf("树的叶子的数量为：%d\n", num);

	//2. 求树的高度 或者说 深度
	int height = getTreeHeight(&nodeA);
	printf("树的高度为：%d\n", height);

	//3. 拷贝二叉树
	struct BinaryNode* newTree = copyTree(&nodeA);

	//递归遍历
	recursion(newTree);

	//4. 释放二叉树
	freeTree(&newTree);
}

int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

二叉树非递归遍历

1. 将根节点入栈
2. 只要栈中元素个数大于0，执行循环
        2.1 弹出栈顶元素
        2.2 如果这个栈顶元素标志为真，输出这个元素并且执行下一次循环
        2.3 如果栈顶元素标志为假，将节点的标志设为真
        2.4 将该节点的右子树，左子树，根 压入到栈中
        2.5 执行下一次循环
执行上述流程，可以得到先序遍历的结果，如果想得到其他二叉树遍历结果，修改2.4步骤即可。

示例

struct BinaryNode
{
	//数据域
	char ch;
	//指针域
	struct BinaryNode* lChild;
	struct BinaryNode* rChild;
	//标志
	int flag;
};
/*
1. 将根节点入栈
2. 只要栈中元素个数大于0，执行循环
	2.1 弹出栈顶元素
	2.2 如果这个栈顶元素标志为真，输出这个元素并且执行下一次循环
	2.3 如果栈顶元素标志为假，将节点的标志设为真
	2.4 将该节点的右子树，左子树，根 压入到栈中
	2.5 执行下一次循环
执行上述流程，可以得到先序遍历的结果，如果想得到其他二叉树遍历结果，修改2.4步骤即可。
*/
void nonRecursion(struct BinaryNode* root) 
{
	//初始化栈
	SeqStack myStack = initSeqStack();
	//将根节点入栈
	pushSeqStack(myStack, root);
	//只要栈中元素个数大于0，执行循环
	while (sizeSeqStack(myStack) > 0) 
	{
		//弹出栈顶元素
		struct BinaryNode* pTop = topSeqStack(myStack);

		//出栈
		popSeqStack(myStack);
		//如果标志为真，直接输出，并且执行下一步循环
		if (pTop->flag == 1) 
		{
			printf("%c ", pTop->ch);
			continue;
		}
		//如果为假，将标志改为真
		pTop->flag = 1;
		//将右子树，左子树，根入栈
		if (pTop->rChild != NULL) 
		{
			pushSeqStack(myStack, pTop->rChild);
		}
		if (pTop->lChild != NULL)
		{
			pushSeqStack(myStack, pTop->lChild);
		}
		pushSeqStack(myStack, pTop);
	}
	//销毁栈
	destroySeqStack(myStack);
}

void test01() 
{
	struct BinaryNode nodeA = { 'A',NULL,NULL,0 };
	struct BinaryNode nodeB = { 'B',NULL,NULL,0 };
	struct BinaryNode nodeC = { 'C',NULL,NULL,0 };
	struct BinaryNode nodeD = { 'D',NULL,NULL,0 };
	struct BinaryNode nodeE = { 'E',NULL,NULL,0 };
	struct BinaryNode nodeF = { 'F',NULL,NULL,0 };
	struct BinaryNode nodeG = { 'G',NULL,NULL,0 };
	struct BinaryNode nodeH = { 'H',NULL,NULL,0 };

	//建立关系
	nodeA.lChild = &nodeB;
	nodeA.rChild = &nodeF;

	nodeB.rChild = &nodeC;

	nodeC.lChild = &nodeD;
	nodeC.rChild = &nodeE;

	nodeF.rChild = &nodeG;

	nodeG.lChild = &nodeH;

	//非递归遍历
	nonRecursion(&nodeA);

}

int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

插入排序

从I = 1位置开始  做外层循环

判断 如果  I -1 > I 将i指向的数据缓存

j开始做内侧循环，找到要插入的位置 将缓存数据插入到 j +1位置上

i++

示例

void insertSort(int arr[], int len) 
{
	for (size_t i = 0; i < len; i++)
	{
		if (arr[i - 1] > arr[i]) 
		{
			int temp = arr[i];
			int j = i - 1;
			for (; j >= 0 && temp < arr[j]; j--) 
			{
				//数据后移
				arr[j + 1] = arr[j];
			}
			arr[j + 1] = temp;
		}
	}
}

void printArray(int arr[], int len) 
{
	for (size_t i = 0; i < len; i++)
	{
		printf("%d\n", arr[i]);
	}
}
void test01() 
{
	int arr[] = { 4,1,2,3,5,7,6 };

	//插入排序
	int len = sizeof(arr) / sizeof(int);
	insertSort(arr, len);

	//打印数据
	printArray(arr, len);
}


int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}
avatar
文章
阅读
粉丝