本文已参与「新人创作礼」活动，一起开启掘金创作之路。

一、一个动机

保护方向信息的方向保持轨迹简化（DPTS）已被证明表现良好，而现有关于 DPTS 的研究 要求用户指定一个容错，在某些情况下用户可能不知道如何正确设置（例如，容错只能在未来某个时间知道，简单地设置一个容错不能满足需要）因为简化的轨迹通常会在许多不同的应用程序中使用，这些应用程序接受不同的误差容限）；

现有的基于位置的轨迹压缩算法，虽然能保证距离误差，但不能保证方向，而基于方向的轨迹压缩算法既能保证方向，也能保证距离；

所以，作者把 根据指定方向误差阈值压缩 这一 Min-Size 问题转换成了 根据指定压缩率寻得达到目标的最小方向误差，即 Min-Error 问题；简单来说，给出了一个存储预算，表示要存储的简化轨迹的最大大小（请注意，存储预算意味着压缩率要求），目标是最小化简化轨迹的误差；

二、两个思想

1. 为了 精确 解决最小化误差问题，探索了 动态规划和二分法 的思想，产生了两种不同的算法，时间复杂度分别为：$O(WN^3)$ 和 $O(CN^2logN)$，其中 W 为存储预算、C 小常数、N 为轨迹长度；
2. 为了降低时间复杂度，开发了一种近似算法：该算法在 O(NlogN) 时间内运行，给出答案的近似值；

三、算法原理

3.1 问题定义

对于文章 Sec 2

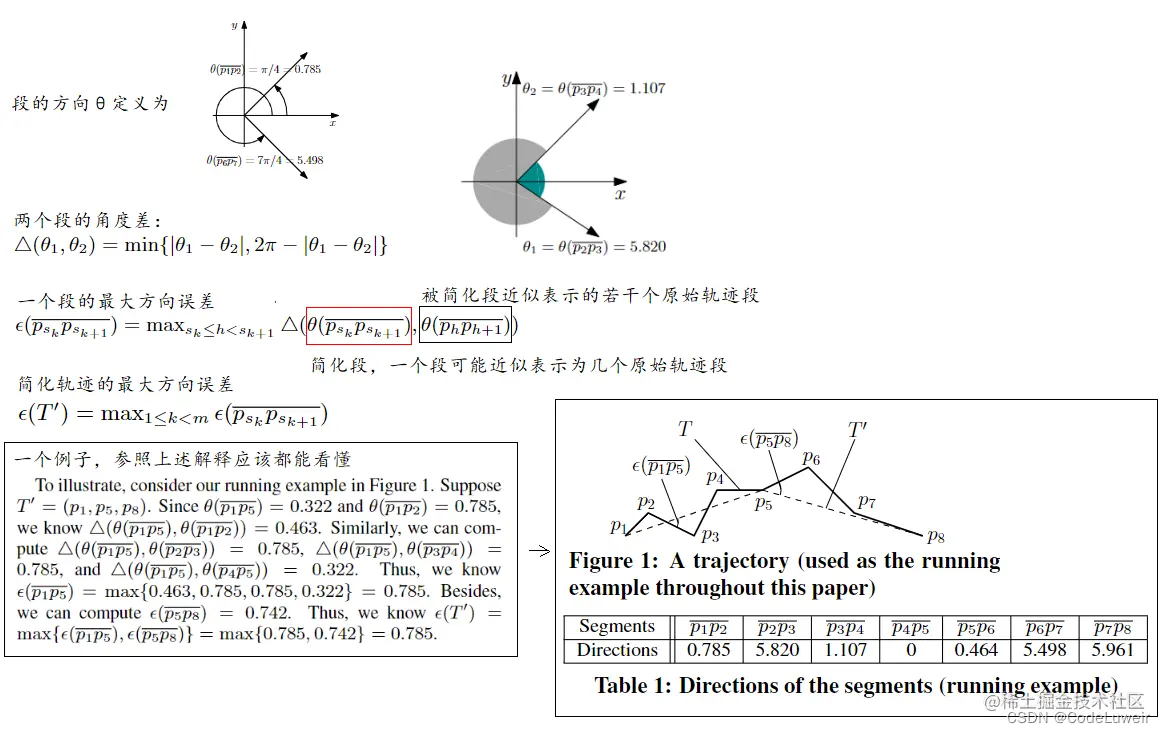
Min-Error 问题：给定一条轨迹 T 和一个正整数 W（存储预算） ，最小误差问题是找到 T 的简化 T ' 使得 |T '|≤W 和 ε(T ') 被最小化；

对于上面那个例子，如果 W=3，并且 T'=(p1,p5,p8) 就是最优解，因为我们找不到任何其他的 T 的简化，其大小最多为 3，其误差小于 $ε(T') (= 0.785)$；

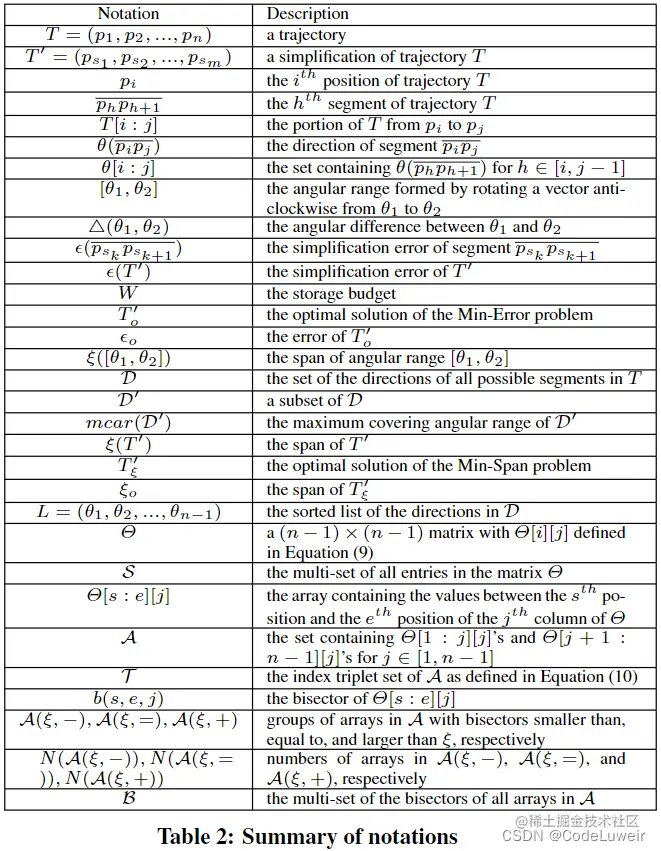
Paper notations

3.2 精确算法

对于给定的原始轨迹 T 和存储预算 W，那么 F 是所有简化轨迹的集合，即 F 包含 W 的指数个简化轨迹，每个简化轨迹有 W 个点；

如何转换为动态规划问题

• 如果 $T'=(p_{s1},p_{s2},...,p_{sm})$是 输入 $T[S_{1}:n]$ 和 $W$ 的最优解，那么 $T''=(p_{s2},...,p_{sm})$ 就是 $T[S_{2}:n]$ 和 $W-1$ 的最优解；
• 如果把它认为是一个函数 func，那么 func(1,n,W)=func(2,n,W-1)+Psi；

怎么把 $O(n^3)$优化为 $O(n^2logn)$

1. Let E be the set containing all $ε(pipj)$ 's for 1 ≤ i < j ≤ n, i.e., $E=ε(pipj)∣1≤i<j≤n$. Note that $∣E∣=O(n2)$，如果直接用 $ε(pskpsk+1)=MAXsk≤h<sk+1 △(θ(pskpsk+1),θ(phph+1))$，那么整个复杂度为 $O(n^3)$；提出 基于 相反方向 的概念，降低它的复杂度为 $O(n^2logn)$；
2. 既然 $ε(pipj)$ 对应于 $θ(pipj)$ 和 $θ[i:j]$ 方向之间的最大角度差。因此，计算 $ε(pipj)$ 可以通过在 $θ[i:j]$ 中找到与 $θ(pipj)$ 角度差最大的方向来完成，这个方向表示为 $θ∗$；
3. 那么，现在的要点是如何快速地找到 $θ∗$；
4. $θ(pipj)−$ 是 $θ(pipj)$ 相反的方向，$θ(pipj)−=[(θ(pipj)+π)mod2π]$，那么 $θ∗$ 就是与 $θ(pipj)−$ 角度差最小的方向，如图5所示：
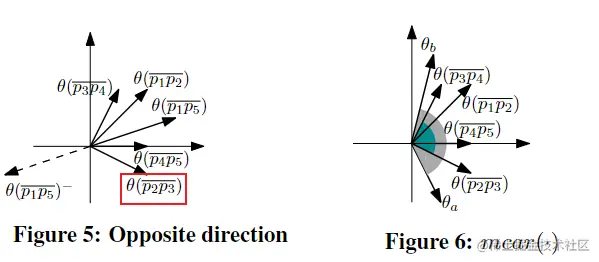
   $θ(p2p3)$ 是 $θ[1:5]$ 中与 $θ(p1p5)$ 的角度差最大的方向，它也是与 $θ(p1p5)−$ 角度差最小的方向；
5. 分两步搜索 $θ∗$：
   1. 首先按升序排列 $θ[i:j]$ 里的方向，排序结果为 $θ1,θ2,θ3,...,θj−1$，这里是 $O(nlogn)$ 的成本；
   2. 然后在排序的列表中找到与 $θ(pipj)−$ 有最小角度差的方向，即 $θ∗$，排序列表找符合条件的某个元素 => 二分查找 $logn$；
6. 总的来说就是，先对所有的 $θ(p1p2),θ(p2p3),...,θ(pn−1pn)$ 按照角度升序排序 = $O(nlogn)$，排序完就定了，这个不需要反复执行；然后对 $O(n2)$ 个 $ε(pipj)$ 实例执行计算，每次计算都是找对应实例的 $θ∗$，每次的成本为 $logn$，因此总成本为 $O(nlogn+n^2logn)=O(n^2logn)$；这个地方很关键；原文如下：

3.3 近似算法 Span-Search

Span-Search：跨度搜索用于解决最小误差问题，该算法在 $O(nlog2n)$ 时间内运行并给出因子近似值； Min-Span 的新问题，其最优解对应于 Min-Error 问题的 2 因子近似；

Span：角度范围 $[θ1,θ2]$ 的跨度 -> $ξ([θ1,θ2])$

$ξ([θ1,θ2])$ 始终>= 0，并且 $ξ([θ1,θ2]) + ξ([θ2,θ1]) = 2\pi$

Let D be the set of the directions of all possible segments in T , i.e., $D = θ[1 : n]$. Note that $|D|= n−1$，就是说 |D| 中段的个数为 n-1 段；

举例：下图中 $D' = θ[1:5] = \{θ(p1p2), θ(p2p3), θ(p3p4), θ(p4p5)\}$，$mcar(D')=[θ(p2p3),θ(p3p4)]$，因为后者覆盖了 $D'$ 中的所有方向；

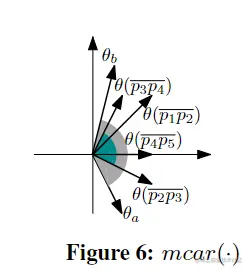
请注意，$mcar(D')$ 的两个边界始终来自 $D'$，否则范围可能会进一步缩小并且它没有最小跨度；

以一个轨迹为例：

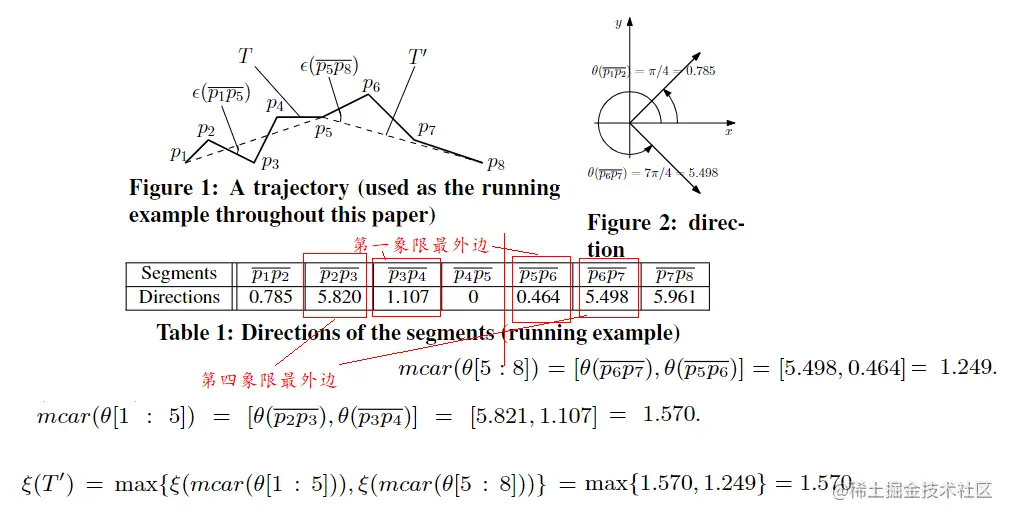
3.3 跨度搜索概述

成对方向差异： $Θ[i][j]= \theta_j - \theta_i$ if $j \ge i$，否则 $Θ[i][j]=2\pi-(\theta_i-\theta_j)$，确保 $Θ$ 均大于0；

下面就是一系列时间复杂度的证明，证明 Span-Search 的复杂度为 $O(nlog^2n)$，公式太多，就不多叙述了，有需要的自行深入分析；

四、实验部分

本文比较的是两个经典的算法：

• wavelet transformation 小波变换，时序数据处理的经典算法
• DP 算法，轨迹数据压缩的经典算法

数据集也是经典的很多人用的数据集：

• Geolife：Geolife3 记录了 182 名用户在 5 年内的户外活动；
• T-Drive：-Drive4 是北京的一组出租车轨迹；

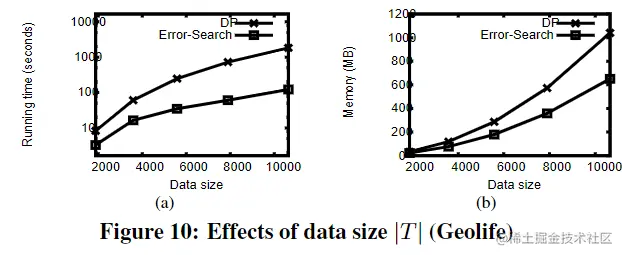
允许时间比 DP 快，我也是有些质疑，DP的复杂度为 $O(n^2)$，而作者的精确算法复杂度为 $O(n^2logn)$，按理说应该没有 DP 快；

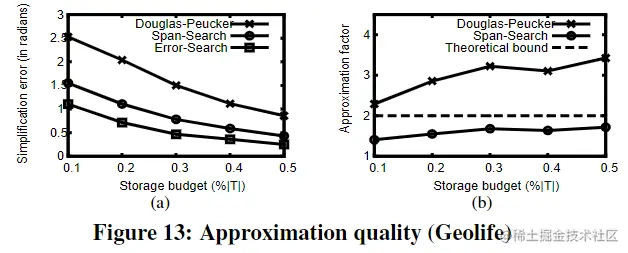
误差衡量一般都是选取对自身有利的指标，想这里它选取的就是方向误差，因为它是基于方向的轨迹压缩算法，而 DP 是基于 PED 距离的轨迹压缩算法，作者应该选取另一个 基于方向 的算法作为基线比较，或者与DP算法再比较一下 PED 误差；

五、最后总结

1. 这篇文章思想是以角度误差为指标来进行轨迹压缩，精确的算法（动态规划）复杂度较高 $O(n^3)$，可以用二分优化，复杂度为 $O(n^2logn)$；后面提供一种近似算法，具有很低的时间复杂度 $O(nlog2n)$；
2. 感觉这篇文章的原理，即使用角度误差为指标进行压缩 不算难，仔细一看就能懂，比较难的是近似算法的证明那部分，这种优化的思路可以学习；
3. 由于我的目的在于浮现他的算法，所以懂了精确算法部分的原理就够了，不考虑时间复杂度，后续有时间再考虑把近似算法也搞出来吧；