1.正则语言的判定

先来看一个例子，
设$\Sigma = \{ 0,1,\cdots,9 \}$，$L \subseteq \Sigma^*$是可以被2或3整除的非负整数的十进制表示的集合（前面没有多余的0）。下面分4个步骤证明$L$是正则的。

1.令$L_1$是非负整数十进制表示的集合。可以写作

由于$L_1$是用正则表达式表示的，故为正则语言。

能用正则表达式表示的语言是正则语言。

2.令$L_2$是可以被2整除的非负整数十进制表示的集合。即以0，2，4，6，8结尾，可以写作

由于$L_1$是正则的且$\Sigma^* \{ 0,2,4,6,8 \}$是正则的，$L_2$同样正则。

正则语言在 并、连接、Kleene星号、补、交 运算下封闭。

3.令$L_3$是可以被3整除的非负整数十进制表示的集合。构造一台有穷自动机如下

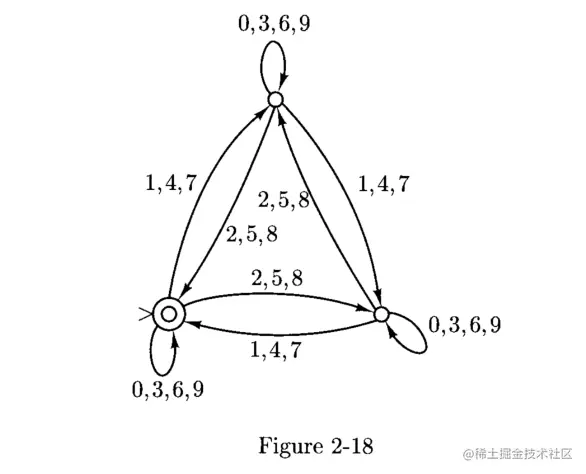
Elements of the Theory of Computation

于是$L_3$是正则的。

一个语言是正则的当且仅当它能被有穷自动机接受

4.最后$L = L_2 \cup L_3$，它是正则语言。

2.非正则语言的判定

先直观地描述性地给出正则语言共有而非正则语言不具备的两条性质：

1. 从左到右扫描一个字符串时，为了确定这个字符串最终是否在该语言中，所需要的存储量必须是有界的、事先固定的且只与该语言有关而与具体的输入字符串无关的。
   例如：$\{ a^nb^n:n \ge 0 \}$不是正则的，因为无法让一台有穷自动机记住到达界限前a的个数以及b的个数并进行比较。

2. 有无穷多个字符串的正则语言用带圈的有穷自动机或含Kleene星号的正则表达式表示。这样的语言一定有具有某种简单的重复构造的无穷子集。
   例如：$\{a^n : n \ge 1且是一个素数\}$不是正则的，因为素数不具备简单的周期性。

下面给出一个形式化的定理能够体现上述两个直观的想法。

---

定理 2.4.1 设$L$是一个正则语言，则存在正整数$n \ge 1$使得任一字符串$w \in L$只要$|w| \ge n$就可以写成$w = xyz$，其中$y \neq e,|xy| \le n$且对每一个$i \ge 0,xy^iz \in L$。

---

证明：由于$L$是正则的，则它被一台有穷自动机$M$接受，设$M$有$n$个状态，$w \in L$是一个长度大于等于$n$的字符串。考虑如下计算过程：

上面的过程存在$n+1$个格局，而最多只有$n$个状态，根据鸽巢原理，必然有至少一个状态能够一步回到自己本身，即存在一个圈。那么在这个状态上可以重复任意次都保证语言被自动机接受。

来看一些例子：

例2.4.2
性质1对应的例子$L = \{a^i b^i:i \ge 0\}$，考虑字符串$w = a^nb^n \in L$。根据定理，可以把它重写为$w = xyz$，令$y = a^i,i>0$即可满足$|xy| \le n$且$y \neq e$，但是考虑$xy^0z = xz = a^{n-1}b^n \notin L$，矛盾。

例2.4.3
性质2对应的例子$L = \{a^n:n是素数\}$，考虑$x = a^p,y = a^q,z = a^r$，则$p+nq+r$需要为素数，但是令$n = p+2q+r+2$，便存在$p+nq+r = (q+1)(q+2q+r)$是两个大于1的自然数的乘积，矛盾。

例2.4.4

有时使用封闭性证明一个语言不是正则的。

令$L = \{ w \in \{a,b\}^*:w中a,b个数相同 \}$。 由于$L \; \cap \; a^*b^* = \{a^nb^n:n \ge 0\}$不是正则的，则$L$也不是正则的。