单向链表企业版

设计思路：

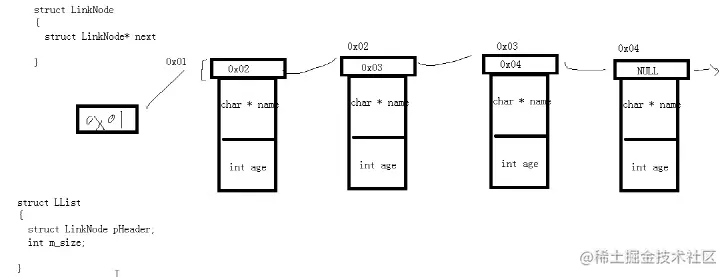
节点只维护一个指针域，用户的数据预留前4个字节由底层使用

接口

初始化链表
LinkList initLinkList() 
插入链表
void insertLinkList(LinkList list,int pos, void* data) 
遍历链表
void foreachLinkList(LinkList list,void(*myForeach)(void *))
删除链表（按位置）
void removeByPosLinkList(LinkList list, int pos) 
销毁链表
void destroyLinkList(LinkList list)

示例

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>

//节点结构体
struct LinkNode 
{
	//只维护指针域
	struct LinkNode* next;
};

//链表结构体
struct LList 
{
	struct LinkNode pHeader;
	int mSize;
};

typedef void* LinkList;

//初始化链表
LinkList initLinkList() 
{
	struct LList * myList = malloc(sizeof(struct LList));
	if (myList == NULL) 
	{
		return NULL;
	}

	myList->pHeader.next = NULL;
	myList->mSize = 0;

	return myList;

}

//插入
void insertLinkList(LinkList list,int pos, void* data) 
{
	if (list == NULL) 
	{
		return;
	}
	if (data == NULL) 
	{
		return;
	}
	struct LList* myList = list;
	if (pos <0 || pos>myList->mSize - 1) 
	{
		//无效位置进行尾插
		pos = myList->mSize;
	}
	//用户数据的前4个字节 由我们来使用
	struct LinkNode* myNode = data;

	//找插入节点的前驱节点
	struct LinkNode* pCurrent = &myList->pHeader;
	for (size_t i = 0; i < pos; i++)
	{
		pCurrent = pCurrent->next;
	}
	//pCurrent 是前驱节点位置

	//更改指针指向
	myNode->next = pCurrent->next;
	pCurrent->next = myNode;

	//更新链表长度
	myList->mSize++;
}

//遍历链表
void foreachLinkList(LinkList list,void(*myForeach)(void *))
{
	if (list == NULL) 
	{
		return;
	}
	struct LList* myList = list;

	struct LinkNode* myNode = myList->pHeader.next;

	//帮用户找到下一个节点，用户自己打印
	for (size_t i = 0; i < myList->mSize; i++)
	{
		myForeach(myNode);
		myNode = myNode->next;
	}
}

//删除节点，按位置删除
void removeByPosLinkList(LinkList list, int pos) 
{
	if (list == NULL) 
	{
		return;
	}

	struct LList* myList = list;

	if (pos<0 || pos>myList->mSize - 1) 
	{
		return;
	}

	//找到待删除节点的前驱
	struct LinkNode* pCurrent = &myList->pHeader;
	for (size_t i = 0; i < pos; i++)
	{
		pCurrent = pCurrent->next;
	}
	//记录待删除节点
	struct LinkNode* pDel = pCurrent->next;

	//更改指针指向
	pCurrent->next = pDel->next;
	//不能把pDel free掉，数据是用户去管理开辟的，我们没有权利释放，用户管理释放

	//更新长度
	myList->mSize--;
}

//清空直接把PHeader指向NULL就好了
//销毁数据
void destroyLinkList(LinkList list) 
{
	if (list == NULL) 
	{
		return;
	}

	free(list);
	list = NULL;
}

//测试
struct Person 
{
	void * node; //预留四个字节
	char name[64];
	int age;
};

void myPrintPerson(void* data) 
{
	struct Person* p = data;
	printf("name = %s age =%d\n", p->name, p->age);
}

void test01() 
{
	//初始化链表
	LinkList myList = initLinkList();

	//创建数据
	struct Person p1 = { NULL,"aaa",18 };
	struct Person p2 = { NULL,"bbb",19 };
	struct Person p3 = { NULL,"ccc",20 };
	struct Person p4 = { NULL,"ddd",21 };
	struct Person p5 = { NULL,"eee",22 };

	//插入节点
	insertLinkList(myList, 0, &p1);
	insertLinkList(myList, 0, &p2);
	insertLinkList(myList, 0, &p3);
	insertLinkList(myList, 0, &p4);
	insertLinkList(myList, 0, &p5);

	//遍历链表
	foreachLinkList(myList,myPrintPerson);

	//删除链表
	removeByPosLinkList(myList, 3);

	printf("-----------------\n");

	//遍历链表
	foreachLinkList(myList, myPrintPerson);

	//销毁链表
	destroyLinkList(myList);
	myList = NULL;
}

int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

受限线性表：栈

受限线性表包括栈和队列。

首先它是一个线性表，也就是说，栈元素具有线性关系，即前驱后继关系。只不过**它是一种特殊的线性表**而已。
定义中说是在线性表的表尾进行插入和删除操作，这里表尾是指栈顶（**低地址**），而不是栈底（**高地址**）。

特性：
    它的特殊之处在于限制了这个线性表的插入和删除的位置，它始终只在栈顶进行。
    这也就使得：栈底是固定的，最先进栈的只能在栈底。

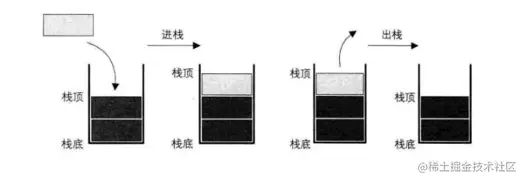
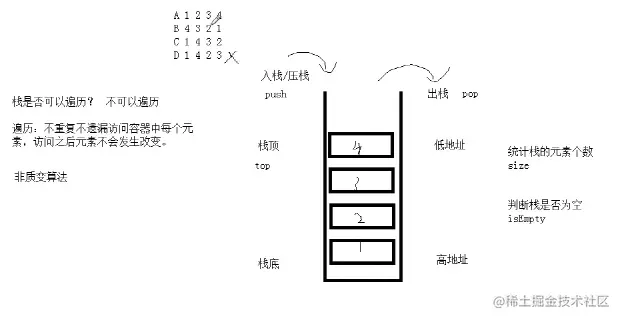
栈可以统计元素个数，可以判断是否为空，但是不能遍历（非质变算法）。

栈：符合先进后出的数据结构

入栈 push

出栈 pop

栈顶 top

栈大小 size

是否为空 isEmpty

栈顶 -高地址 栈底 -低地址

栈不可以遍历，在查看各个元素过程中就已经发生了质变

栈的顺序存储

利用数组模拟出先进后出数据结构

数组中首地址  做栈底 方便数组尾部做插入删除

对外接口

 初始化栈 init
 SeqStack initSeqStack() 
 入栈  push
 void pushSeqStack(SeqStack stack,void * data) 
 出栈  pop
 void popSeqStack(SeqStack stack) 
 栈顶  top
 void* topSeqStack(SeqStack stack) 
 栈大小  size
 int sizeSeqStack(SeqStack stack) 
 是否为空  isEmpty
 int isEmptySeqStack(SeqStack stack) 
 销毁栈 destroy
 void destroySeqStack(SeqStack stack)

示例

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>
#define MAX 1024

struct SStack 
{
	void* data[MAX]; //栈数组

	int mSize; //栈大小
};

typedef void* SeqStack;

//初始化栈
SeqStack initSeqStack() 
{
	struct SStack* myStack = malloc(sizeof(struct SStack));
	if (myStack == NULL) 
	{
		return NULL;
	}
	//初始化数组
	memset(myStack->data, 0, sizeof(void*) * MAX);
	//初始化栈大小
	myStack->mSize = 0;
	return myStack;
}
//入栈
void pushSeqStack(SeqStack stack,void * data) 
{
	//入栈本质   --数组尾插
	if (stack == NULL) 
	{
		return;
	}
	if (data == NULL) 
	{
		return;
	}
	struct SStack* myStack = stack;
	if (myStack->mSize == MAX) 
	{
		return;
	}

	myStack->data[myStack->mSize] = data;

	myStack->mSize++;
}
//出栈
void popSeqStack(SeqStack stack) 
{
	//出栈本质 --数组尾删
	if (stack == NULL) 
	{
		return;
	}

	struct SStack* myStack = stack;

	if (myStack->mSize == 0) 
	{
		return;
	}
	myStack->data[myStack->mSize - 1] = NULL;

	//更新栈的大小
	myStack->mSize--;
}
//返回栈顶
void* topSeqStack(SeqStack stack) 
{
	if (stack == NULL) 
	{
		return NULL;
	}

	struct SStack* myStack = stack;
	if (myStack->mSize == 0) 
	{
		return NULL;
	}
	return myStack->data[myStack->mSize - 1];
}
//返回栈大小
int sizeSeqStack(SeqStack stack) 
{
	if (stack == NULL) 
	{
		return -1;
	}
	struct SStack* myStack = stack;

	return myStack->mSize;
}
//判断栈是否为空
int isEmptySeqStack(SeqStack stack) 
{
	if (stack == NULL) 
	{
		return -1;//返回-1，代表真，空栈
	}

	struct SStack* myStack = stack;

	if (myStack->mSize == 0) 
	{
		return 1;
	}
	return 0;//返回0 代表为 假 不是空栈
}
//销毁栈
void destroySeqStack(SeqStack stack) 
{
	if (stack == NULL)
	{
		return;
	}
	free(stack);
}

struct Person 
{
	char name[64];
	int age;
};

void test01()
{
	//初始化栈
	SeqStack myStack = initSeqStack();
	//创建数据
	struct Person p1 = { "aaa",18 };
	struct Person p2 = { "bbb",19 };
	struct Person p3 = { "ccc",20 };
	struct Person p4 = { "ddd",21 };
	struct Person p5 = { "eee",22 };

	//入栈
	pushSeqStack(myStack, &p1);
	pushSeqStack(myStack, &p2);
	pushSeqStack(myStack, &p3);
	pushSeqStack(myStack, &p4);
	pushSeqStack(myStack, &p5);
	printf("栈的元素个数为：%d\n", sizeSeqStack(myStack));
	//每个栈弹出看一下
	while (isEmptySeqStack(myStack) == 0) //栈不为空，查看栈顶元素，出栈
	{
		struct Person* p = topSeqStack(myStack);
		printf("name = %s age = %d\n", p->name, p->age);

		//出栈
		popSeqStack(myStack);
	}

	printf("栈的元素个数为：%d\n", sizeSeqStack(myStack));
}

int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

栈的顺序存储分文件编写

可以通过将数据结构的结构体放在实现的.c文件而非头文件中，防止用户在使用中发现数据结构。

栈的链式存储

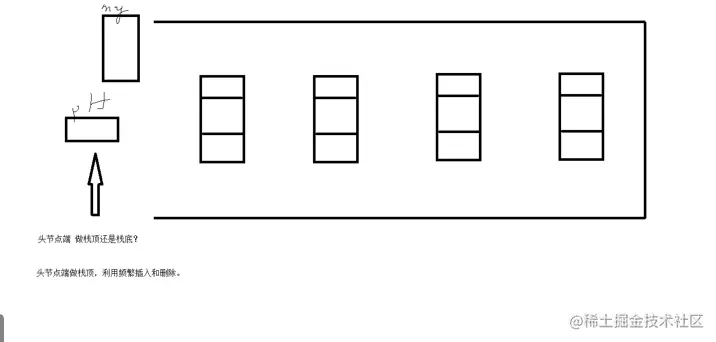
解析图

利用链表模拟出先进后出的数据结构

头节点端做栈顶 比较方便做入栈和出栈

对外接口

初始化栈 init

入栈  push

出栈  pop

栈顶  top

栈大小  size

是否为空  isEmpty

销毁栈 destroy

示例

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <time.h>
#include <Windows.h>

//节点结构体
struct stackNode 
{
	struct stackNode* next;
};

//栈的结构体
struct LStack
{
	struct stackNode pHeader;
	int mSize;
};

typedef void* LinkStack;

//初始化
LinkStack initLinkStack()
{
	struct LStack* myStack = malloc(sizeof(struct LStack));
	if (myStack == NULL) 
	{
		return NULL;
	}

	myStack->pHeader.next = NULL;
	myStack->mSize = 0;
	return myStack;
}
 
//入栈
void pushLinkStack(LinkStack stack, void* data) 
{
	//入栈本质 - 链表头插
	if (stack == NULL) 
	{
		return;
	}
	if (data == NULL) 
	{
		return;
	}
	struct LStack* myStack = stack;
	//将用户数据取出前4字节用
	struct stackNode* myNode = data;

	//更改指针指向
	myNode->next = myStack->pHeader.next;
	myStack->pHeader.next = myNode;

	//更改链表长度
	myStack->mSize++;
}
//出栈
void popLinkStack(LinkStack stack) 
{
	if (stack == NULL)
	{
		return;
	}

	struct LStack* myStack = stack;

	if (myStack->mSize==0) 
	{
		return;
	}
	//更改指针指向
	//缓存第一个有数据节点
	struct stackNode* pFirst = myStack->pHeader.next;
	myStack->pHeader.next = pFirst->next;

	//更改链表长度
	myStack->mSize--;
}
//返回栈顶元素
void* topLinkStack(LinkStack stack) 
{
	if (stack == NULL)
	{
		return NULL;
	}

	struct LStack* myStack = stack;
	if (myStack->mSize == 0)
	{
		return 0;
	}
	return myStack->pHeader.next;
}
//返回栈个数
int sizeLinkStack(LinkStack stack) 
{
	if (stack == NULL)
	{
		return NULL;
	}

	struct LStack* myStack = stack;

	return myStack->mSize;
}
//判断是否为空
int isEmptyLinkStack(LinkStack stack) 
{
	if (stack == NULL)
	{
		return -1;
	}
	struct LStack* myStack = stack;

	if (myStack->mSize == 0) 
	{
		return 1;
	}
	return 0;
}
//销毁
void destroyLinkStack(LinkStack stack) 
{
	if (stack == NULL)
	{
		return ;
	}
	free(stack);
	stack = NULL;
}

struct Person
{
	void* node; //预留四个字节
	char name[64];
	int age;
};

void test01()
{
	//初始化栈
	LinkStack myStack = initLinkStack();
	//创建数据
	struct Person p1 = {NULL, "aaa",18 };
	struct Person p2 = { NULL,"bbb",19 };
	struct Person p3 = { NULL,"ccc",20 };
	struct Person p4 = { NULL,"ddd",21 };
	struct Person p5 = { NULL,"eee",22 };

	//入栈
	pushLinkStack(myStack, &p1);
	pushLinkStack(myStack, &p2);
	pushLinkStack(myStack, &p3);
	pushLinkStack(myStack, &p4);
	pushLinkStack(myStack, &p5);
	printf("栈的元素个数为：%d\n", sizeLinkStack(myStack));
	//每个栈弹出看一下
	while (isEmptyLinkStack(myStack) == 0) //栈不为空，查看栈顶元素，出栈
	{
		struct Person* p = topLinkStack(myStack);
		printf("name = %s age = %d\n", p->name, p->age);

		//出栈
		popLinkStack(myStack);
	}

	printf("栈的元素个数为：%d\n", sizeLinkStack(myStack));
}


int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

栈的应用（案例）

就近匹配

1. 从第一个字符开始扫描所有的字符
2. 遇到普通字符直接忽略，遇到左括号入栈
3. 遇到右括号
    1） 如果栈中有元素，出栈
    2） 如果栈中没有元素，立即停止，并且报错
4. 当所有的字符都扫描完毕，查看栈中内容
    1） 如果是空栈，没有问题
    2） 如果不是空栈，报错，左括号没有匹配到对应的右括号

示例

#include "seqStack.h"

//从第一个字符开始扫描
//当遇见普通字符时忽略，
//当遇见左括号时压入栈中
//当遇见右括号时从栈中弹出栈顶符号，并进行匹配
//匹配成功：继续读入下一个字符
//匹配失败：立即停止，并报错
//结束：
//成功 : 所有字符扫描完毕，且栈为空
//失败：匹配失败或所有字符扫描完毕但栈非空
int isLeft(char ch) 
{
	return ch == '(';
}
int isRight(char ch)
{
	return ch == ')';
}
void printError(char* str, char* errMsg,char *pos) 
{
	printf("错误信息：%s\n", errMsg);
	printf("%s\n", str);
	//计算打印的空格的数量
	int num = pos - str;
	for (size_t i = 0; i < num; i++)
	{
		printf(" ");
	}
	printf("^");
}

void test01() 
{
	char* str = "5+5*(6)+9/3*1-(1+3)";
	char* p = str;

	//初始化栈
	SeqStack myStack = initSeqStack();

	while (*p != '\0')
	{
		//如果是左括号，入栈
		if (isLeft(*p)) 
		{
			//入栈
			pushSeqStack(myStack, p);
		}
		//如果是有括号
		if (isRight(*p)) 
		{
			//栈中有元素
			if (sizeSeqStack(myStack) > 0) 
			{
				popSeqStack(myStack);
			}
			else 
			{
				//右括号中没有匹配到对应的左括号，立即停止，并报错
				printError(str, "右括号没有匹配到左括号",p);
				break;
			}
		}
		p++;
	}
	//遍历结束，判断是否有 左括号没有匹配到对应的右括号
	while(sizeSeqStack(myStack)>0)
	{
		printError(str, "左括号没有匹配到对应的右括号", topSeqStack(myStack));
		//出栈
		popSeqStack(myStack);
	}

	//销毁栈
	destroySeqStack(myStack);
	myStack = NULL;
}
int main(void)
{
	test01();
	system("pause");
	return EXIT_SUCCESS;
}

中缀表达式转后缀表达式运算

中缀表达式转后缀表达式

遍历中缀表达式中的数字和符号：

对于数字：直接输出

对于符号：
    左括号：进栈 
    运算符号：与栈顶符号进行优先级比较
    若栈顶符号优先级低：此符号进栈 
    （默认栈顶若是左括号，左括号优先级最低）
    若栈顶符号优先级不低：将栈顶符号弹出并输出，之后进栈
    右括号：将栈顶符号弹出并输出，直到匹配左括号,将左括号和右括号同时舍弃
    
遍历结束：将栈中的所有符号弹出并输出

基于后缀表达式运算

遍历后缀表达式中的数字和符号

对于数字：进栈

对于符号：
    从栈中弹出右操作数
    从栈中弹出左操作数
    根据符号进行运算
    将运算结果压入栈中

C++笔记day22 单向链表 受限线性表：栈

单向链表企业版

设计思路：

接口

示例

受限线性表：栈

栈：符合 先进后出的数据结构

栈的顺序存储

利用数组模拟出 先进后出数据结构

对外接口

示例

栈的顺序存储 分文件编写

栈的链式存储

利用链表模拟出 先进后出的数据结构

对外接口

示例

栈的应用（案例）

就近匹配

示例

中缀表达式转后缀表达式运算

中缀表达式转后缀表达式

基于后缀表达式运算

C++笔记day22 单向链表受限线性表：栈

栈：符合先进后出的数据结构

利用数组模拟出先进后出数据结构

栈的顺序存储分文件编写

利用链表模拟出先进后出的数据结构