用于ML的K-最近的邻居算法

k-nearest neighbors（kNN）算法是一个简单的工具，可用于金融、医疗、推荐系统等领域的一些实际问题。这篇博文将介绍什么是kNN，它如何工作，以及如何在机器学习项目中实现它。

什么是k-nearest neighbors分类器？

k-近邻分类器（kNN）是一种非参数化的监督机器学习算法。它是基于距离的：它根据物体的近邻类别进行分类。kNN最常被用于分类，但也可以应用于回归问题。

**什么是有监督的机器学习模型？**在监督模型中，学习是由训练集中的标签引导的。为了更好地了解它的工作原理，请查看我们对监督学习原理的详细解释。

非参数化意味着在模型的训练步骤中没有对参数进行微调。虽然k在某种意义上可以被认为是一个算法参数，但它实际上是一个超参数。它是手动选择的，在训练和推理时都保持固定。

k-近邻算法也是非线性的。与线性回归等简单模型相比，它在自变量（x）和因变量（y）之间的关系不是一条直线的情况下，可以很好地工作。

什么是k-nearest neighbors中的k？

kNN中的参数k指的是分类时考虑的标记点（邻居）的数量。k的值表示用于确定结果的这些点的数量。我们的任务是计算距离并确定哪些类别与我们的未知实体最接近。

kNN分类算法是如何工作的？

k-nearest neighbors的主要概念如下。给定一个我们不知道类别的点，我们可以尝试了解我们的特征空间中哪些点与它最接近。这些点就是k-最近的邻居。由于相似的东西在特征空间中占据相似的位置，所以这个点很可能与它的邻居属于同一类别。在此基础上，有可能将一个新的点分类为属于一个或另一个类别。

kNN算法的步骤如下

提供一个训练集

训练集是一组用于训练模型的标记数据。你可以通过手动标注数据来创建训练集，或者使用公共资源中的标注数据库，比如这个。一个好的做法是，使用大约75%的可用数据进行训练，25%作为测试集。

寻找k-最近的邻居

寻找一条记录的k-nearest neighbors意味着识别那些在共同特征方面与它最相似的记录。这一步也被称为相似性搜索或距离计算。

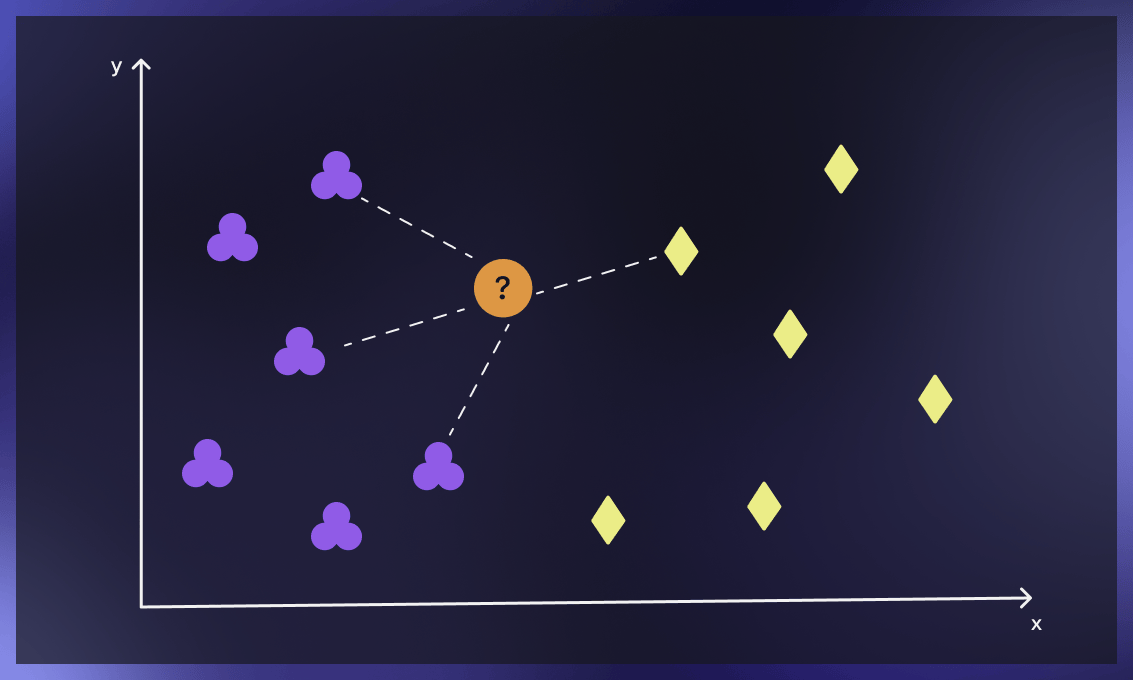
分类点

对于分类问题，算法根据多数票分配类别标签，也就是说，应用邻居中出现频率最高的标签。对于回归问题，使用平均值来确定k个最近的邻居。

在完成上述步骤后，模型会提供结果。请注意，对于分类问题，我们使用的是离散值，所以输出将是描述性的，例如 "喜欢明亮的颜色"。

对于回归问题，应用的是连续值，这意味着输出将是一个浮动的数字。

我们可以通过观察模型的预测和估计与测试集中的已知类别的匹配程度来评估结果的准确性。

如何确定k邻居分类器中的k值？

最佳的k值将帮助你实现模型的最大精度。然而，这个过程总是充满挑战。

最简单的解决方案是尝试k值，并找到在测试集上带来最佳结果的那一个。为此，我们遵循以下步骤：

1. 选择一个随机的k值。在实践中，k通常在3到10之间随机选择，但没有严格的规则。一个小的k值会导致不稳定的决策边界。大的k值通常会导致决策边界的平滑化，但不一定会带来更好的指标。因此，这总是关于试验和错误。

2. 试用不同的k值，并注意它们在测试集上的准确性。

3. 选择错误率最低的k，并实施该模型。

在更复杂的情况下选取k

在出现异常情况或大量邻居紧密围绕未知点的情况下，我们需要找到不同的解决方案来计算k，既要有时间又要有成本效益。

主要的限制与计算资源有关：数据集中的对象越多，选择适当的k的成本就越高。此外，对于大数据集，我们通常在一个多参数的优化设置中工作。我们在这里的目标不仅是通过在元训练中选择合适的k来最大化模型质量，而且要实现更快的模型推理。如果k越大，就需要更多的推理时间，这在大数据集中可能会构成一个问题。

下面我们介绍一些适合这些情况的选择k的高级方法。

1.平方根法

最佳的K值可以计算为训练数据集中样本总数的平方根。使用误差图或准确率图来找到最有利的K值。KNN在多标签类中表现良好，但在有许多离群值的结构中，它可能会失败，你需要使用其他方法。

2.交叉验证法（肘部法）

从k=1开始，然后进行交叉验证（5到10倍--这些数字是常见的做法，因为它们在计算工作和统计有效性之间提供了一个良好的平衡），并评估准确性。不断重复同样的步骤，直到你得到一致的结果。随着k的增加，误差通常会减少，然后稳定下来，然后再增长。最佳的k位于稳定区的起点。

你可以看下面对这个方法的详细解释。

K-距离是如何计算的？

K-距离是数据点和给定查询点之间的距离。为了计算它，我们必须选择一个距离度量。

下面解释了一些最流行的度量。

欧几里得距离

两点之间的欧几里得距离是连接它们的直线段的长度。这个最常见的距离度量适用于实值向量。

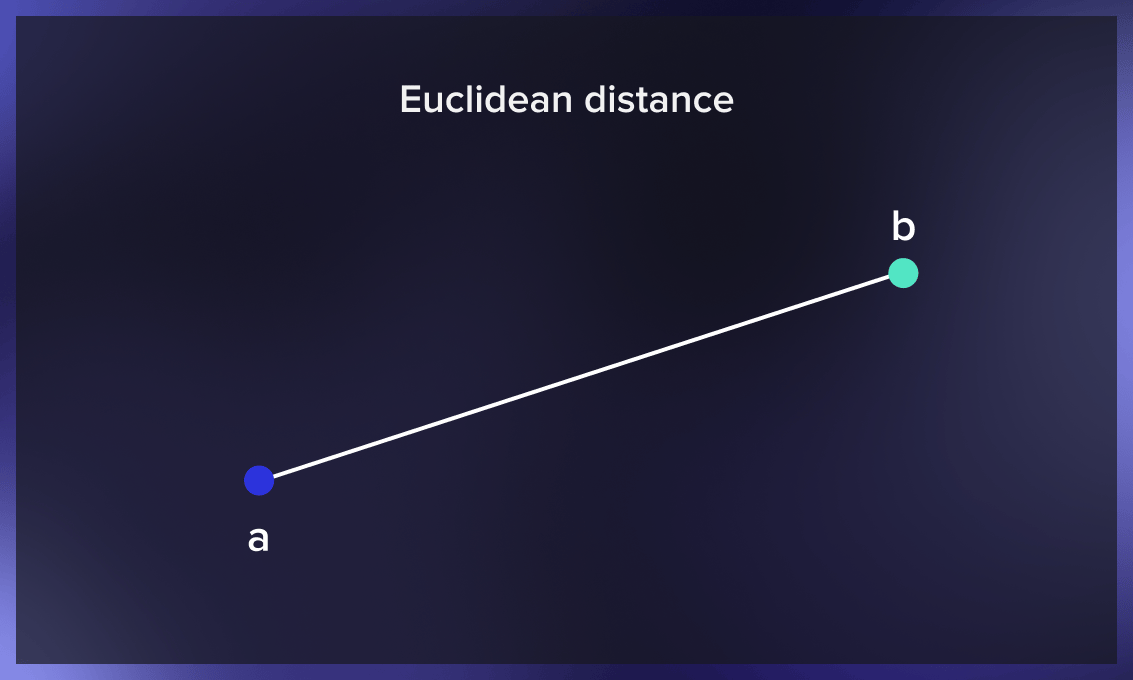
曼哈顿距离

两点之间的曼哈顿距离是每一点的x和y坐标之间的绝对差异之和。用于测量最小的距离，通过对一个城市中从一个地点到另一个地点所需的所有间隔的长度进行求和，它也被称为出租车距离。

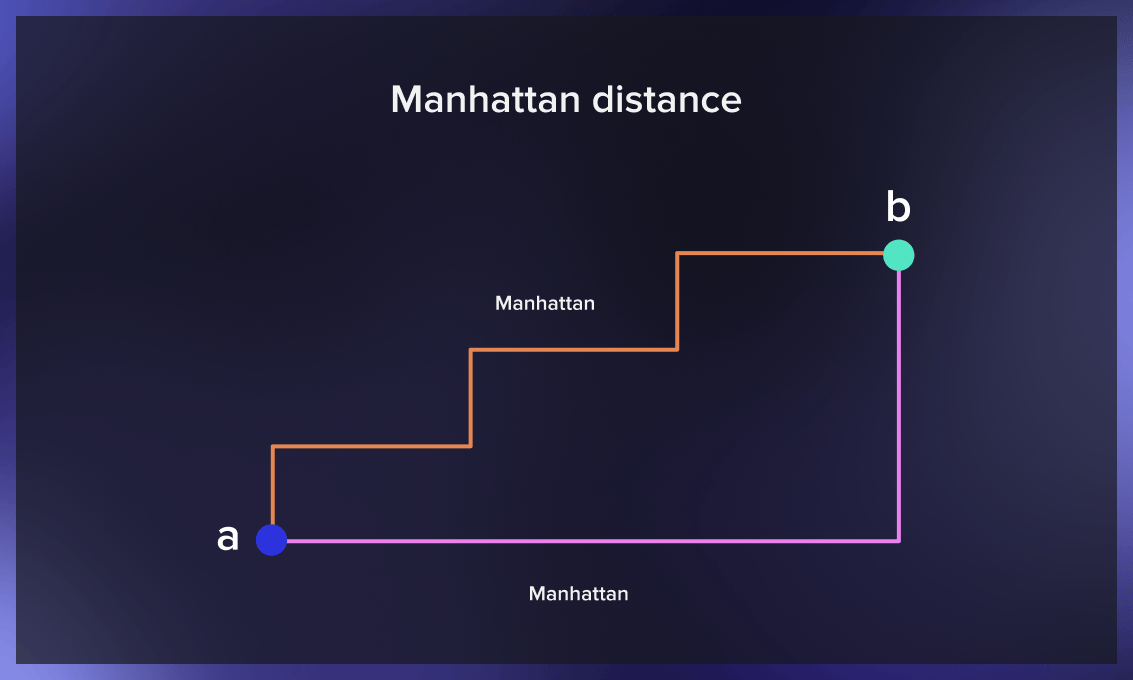
闵科夫斯基距离

闵可夫斯基距离概括了欧几里得和曼哈顿的距离。它增加了一个叫做 "顺序 "的参数，允许计算不同的距离量度。闵可夫斯基距离表示规范化向量空间中两点之间的距离

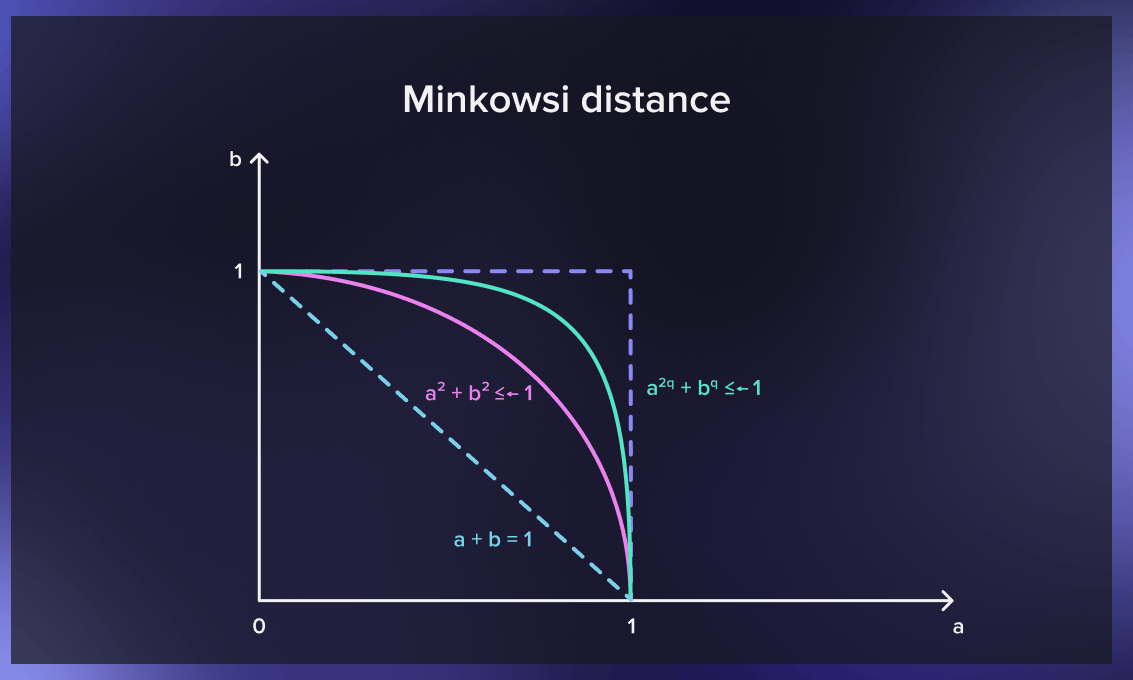
汉明距离

汉明距离用于比较两个二进制向量（也叫数据串或比特串）。为了计算它，数据首先要被翻译成二进制系统。

使用Python的K-近邻

让我们来看看这个分类器在实践中是如何工作的。

第一个步骤

首先，我们需要生成数据，然后在上面运行分类器：

import numpy as np
from typing import Tuple

def generate_data(center_scale: float, cluster_scale: float, class_counts: np.ndarray,
                  seed: int = 42) -> Tuple[np.ndarray, np.ndarray]:
    # Fix a seed to make experiment reproducible
    np.random.seed(seed)
    points, classes = [], []
    for class_index, class_count in enumerate(class_counts):
        # Generate the center of the cluster and its points centered around it
        current_center = np.random.normal(scale=center_scale, size=(1, 2))
        current_points = np.random.normal(scale=cluster_scale, size=(class_count, 2)) + current_center
        # Assign them to the same class and add those points to the general pool
        current_classes = np.ones(class_count, dtype=np.int64) * class_index
        points.append(current_points)
        classes.append(current_classes)
    # Concatenate clusters into a single array of points
    points = np.concatenate(points)
    classes = np.concatenate(classes)
    return points, classes

points, classes = generate_data(2, 0.75, [40, 40, 40], seed=42)

为了绘制生成的数据，你可以运行下面的代码：

import matplotlib.pyplot as plt
plt.style.use('bmh')

def plot_data(points: np.ndarray, classes: np.ndarray) -> None:
    fig, ax = plt.subplots(figsize=(5, 5), dpi=150)
    scatter = ax.scatter(x=points[:, 0], y=points[:, 1], c=classes, cmap='prism', edgecolor='black')
    # Generate a legend based on the data and plot it
    legend = ax.legend(*scatter.legend_elements(), loc="lower left", title="Classes")
    ax.add_artist(legend)
    ax.set_title("Generated dataset")
    ax.set_xticks([])
    ax.set_yticks([])
    plt.show()

plot_data(points, classes)

下面是这段代码产生的图像的例子：

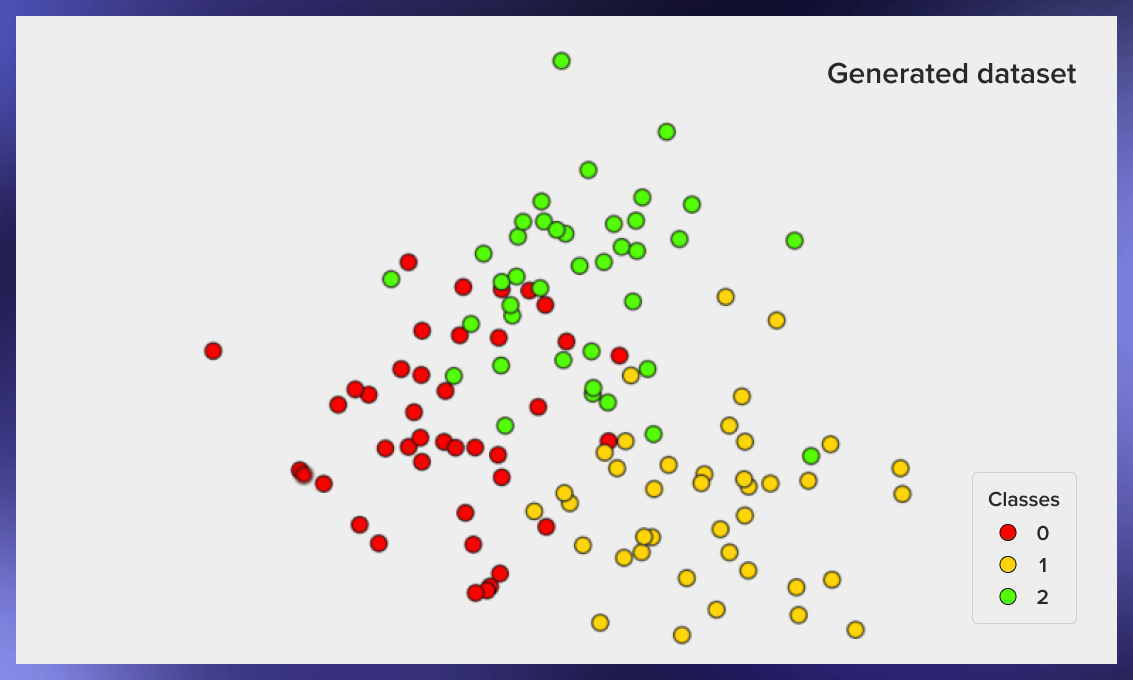
如何分割训练和测试样本

现在我们有一个标记的对象集，每个对象都被分配到一个类别。我们需要将这个集合分成两部分：一个训练集和一个测试集。下面的代码就是用于此的：

from sklearn.model_selection import train_test_split

points_train, points_test, classes_train, classes_test = train_test_split(
    points, classes, test_size=0.3
)

分类器的实现

现在我们有了训练样本，我们可以实现分类器算法：

from collections import Counter

def classify_knn(
    points_train: np.ndarray,
    classes_train: np.ndarray,
    points_test: np.ndarray,
    num_neighbors: int
) -> np.ndarray:
    classes_test = np.zeros(points_test.shape[0], dtype=np.int64)
    for index, test_point in enumerate(points_test):
        # Compute Euclidean norm between the test point and the training dataset
        distances = np.linalg.norm(points_train - test_point, ord=2, axis=1)
        # Collect the closest neighbors indices based on the distance calculated earlier
        neighbors = np.argpartition(distances, num_neighbors)[:num_neighbors]
        # Get the classes of those neighbors and assign the most popular one to the test point
        neighbors_classes = classes_train[neighbors]
        test_point_class = Counter(neighbors_classes).most_common(1)[0][0]
        classes_test[index] = test_point_class
    return classes_test

classes_predicted = classify_knn(points_train, classes_train, points_test, 3)

执行的例子

现在我们可以评估我们的分类器工作得如何。为了做到这一点，我们生成数据，将其分成一个训练集和一个测试集，对测试集中的对象进行分类，并将测试集中的类别的实际值与分类后的值进行比较：

def accuracy(classes_true, classes_predicted):
    return np.mean(classes_true == classes_predicted)

knn_accuracy = accuracy(classes_test, classes_predicted)

#> knn_accuracy
#  0.8055555555555556

现在我们可以用图形显示分类器的工作。在下面的图片中，我们使用了3个类，每个类有40个元素，算法的k值被设定为3：

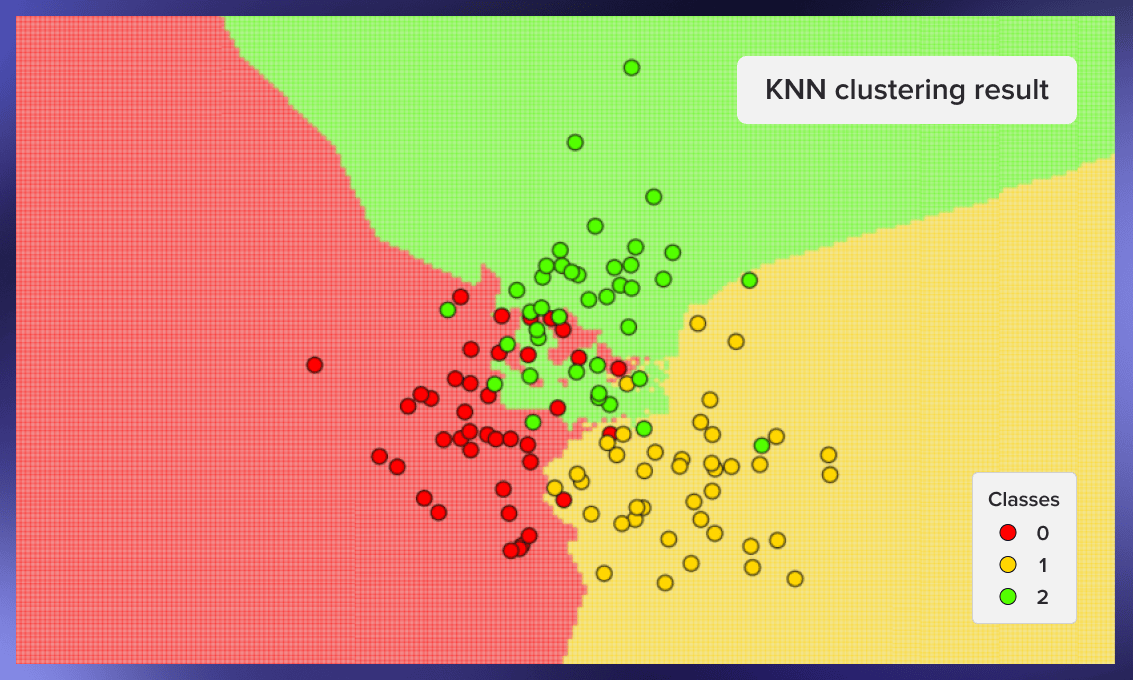
为了创建这些图形，我们可以使用以下代码：

def knn_prediction_visualisation(
    points: np.ndarray,
    classes: np.ndarray,
    num_neighbors: int
) -> None:
    x_min, x_max = points[:, 0].min() - 1, points[:, 0].max() + 1
    y_min, y_max = points[:, 1].min() - 1, points[:, 1].max() + 1
    step = 0.05


    # Prepare a mesh grid of the plane to cluster
    mesh_test_x, mesh_test_y = np.meshgrid(
        np.arange(x_min, x_max, step), np.arange(y_min, y_max, step)
    )
    points_test = np.stack([mesh_test_x.ravel(), mesh_test_y.ravel()], axis=1)
    # Predict clusters and prepare the results for the plotting
    classes_predicted = classify_knn(points, classes, points_test, num_neighbors)
    mesh_classes_predicted = classes_predicted.reshape(mesh_test_x.shape)


    # Plot the results
    fig, ax = plt.subplots(figsize=(5, 5), dpi=150)
    ax.pcolormesh(mesh_test_x, mesh_test_y, mesh_classes_predicted,
                  shading='auto', cmap='prism', alpha=0.4)
    scatter = ax.scatter(x=points[:, 0], y=points[:, 1], c=classes,
                         edgecolors='black', cmap='prism')
    legend = ax.legend(*scatter.legend_elements(), loc="lower left", title="Classes")
    ax.set_title("KNN clustering result")
    ax.set_xticks([])
    ax.set_yticks([])


    plt.show()

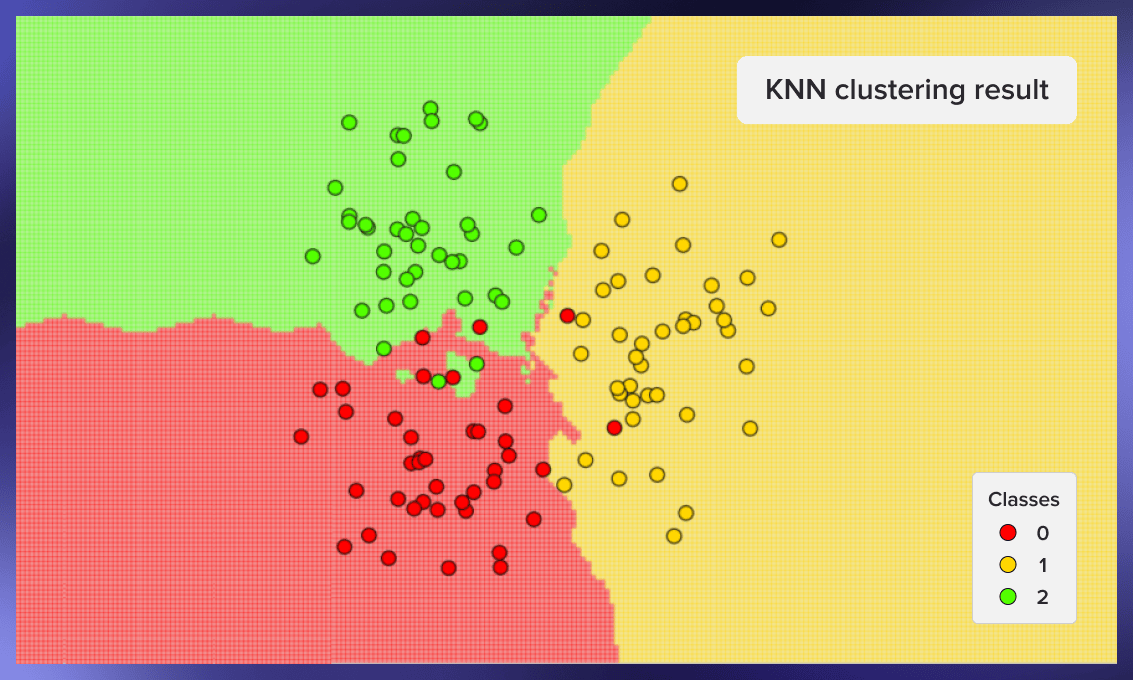
knn_prediction_visualisation(points, classes, 3)

下面是其他一些聚类的例子--第一个来自种子59 ，第二个来自种子0xdeadbeef ，第三个来自种子777：

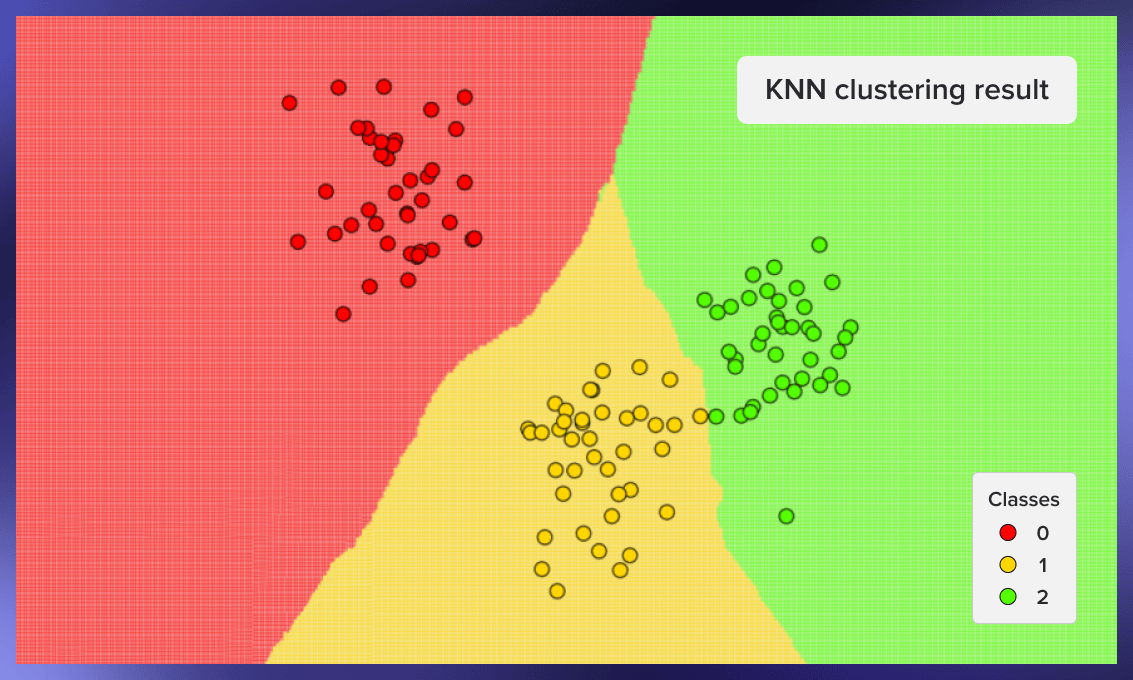
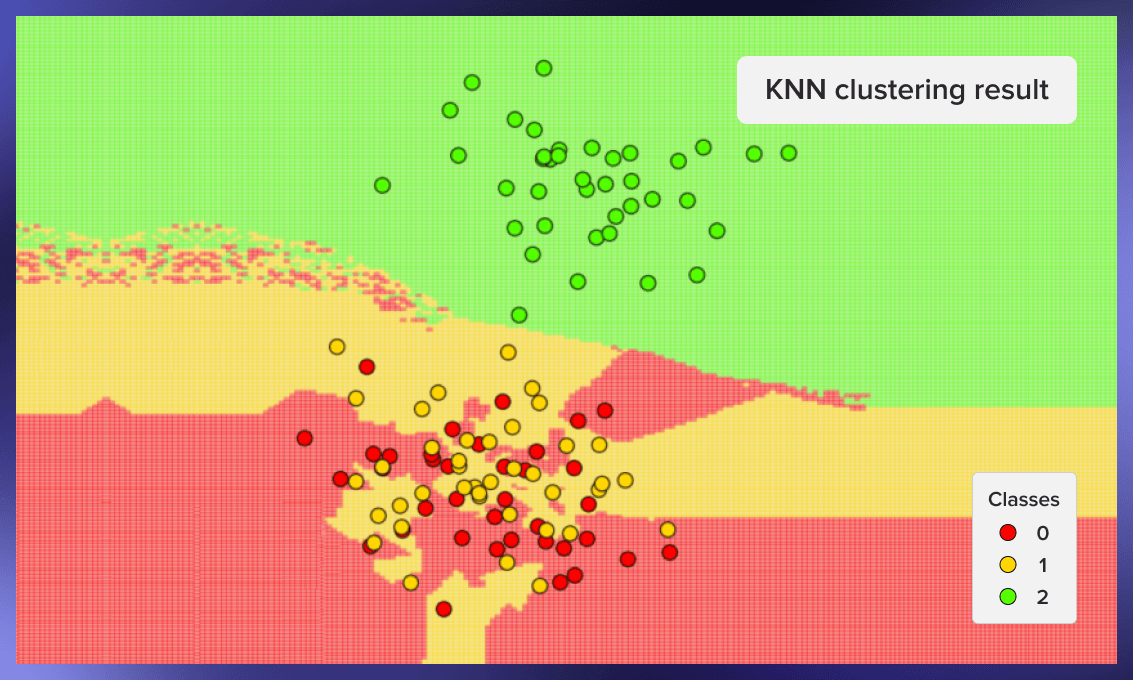
kNN的优点和缺点

kNN的主要优点是开发速度快，解释简单：

• 它可以用于分类和回归问题。
• kNN很容易理解和实现，不需要训练期。
• 研究人员不需要对两个例子的相似性或不相似性有最初的假设。
• K-近邻只在对数据集进行查询后建立模型。
• 该算法可以在推理时间内快速有效地进行比对，这对大型数据集来说特别有用。

然而，该算法也有其弱点：

• kNN比其他分类算法更耗费内存，因为它需要你加载整个数据集来运行计算，这增加了计算时间和成本。
• k-近邻算法在更复杂的任务上表现得更差，比如文本分类。
• 它需要在每个维度上进行特征缩放（规范化和标准化）。

实际应用

用于сar制造的K-近邻方法

一个汽车制造商设计了一个新的卡车和轿车的原型。为了确定其成功的机会，该公司必须找出市场上目前哪些车辆与原型车最相似。他们的竞争对手是他们的 "最近的邻居"。为了识别它们，汽车制造商需要输入数据，如价格、马力、发动机尺寸、轴距、车身重量、油箱容量等，并对现有车型进行比较。kNN算法根据复杂的多特征原型与类似竞争对手产品的接近程度对其进行分类。

电子商务中的kNN

K-近邻是冷启动网店推荐系统的一个很好的解决方案，但随着数据集的增长，通常需要更先进的技术。该算法可以选择特定客户喜欢的商品，或者根据客户行为数据预测他们的行为。例如，kNN可以快速判断一个新访客是否可能进行交易。

kNN在教育方面的应用

另一个kNN的应用是根据学生的行为和课堂出勤率对学生群体进行分类。在k-近邻分析的帮助下，有可能确定哪些学生有可能辍学或提前挂科。这些见解将使教育者和课程管理者能够及时采取措施，激励和帮助他们掌握材料。

经验之谈

kNN算法是流行的、有效的，并且相对容易实现和解释。它可以有效地解决复杂的多变量案例的分类和回归任务。尽管出现了许多先进的替代方案，但它仍然保持着在最佳ML分类器中的地位。