数据结构和算法

---

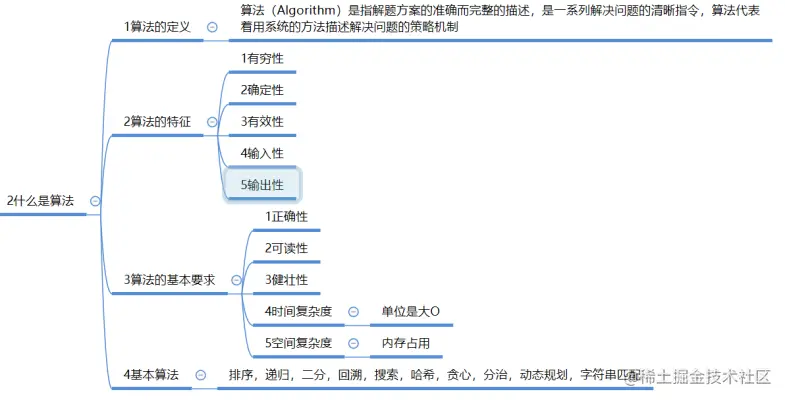
一,算法复杂度

1,时间复杂度是指执行算法所需要的计算工作量
2,空间复杂度是指执行算法所需要的内存空间
3,算法复杂度常用大O符号表示
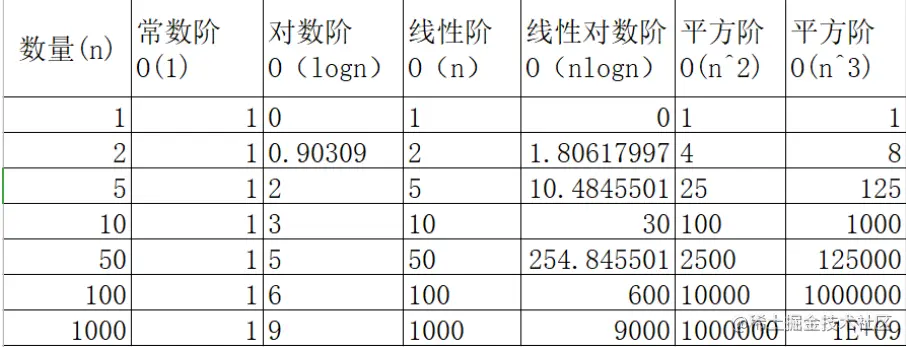
4,不同算法复杂度的差异

---

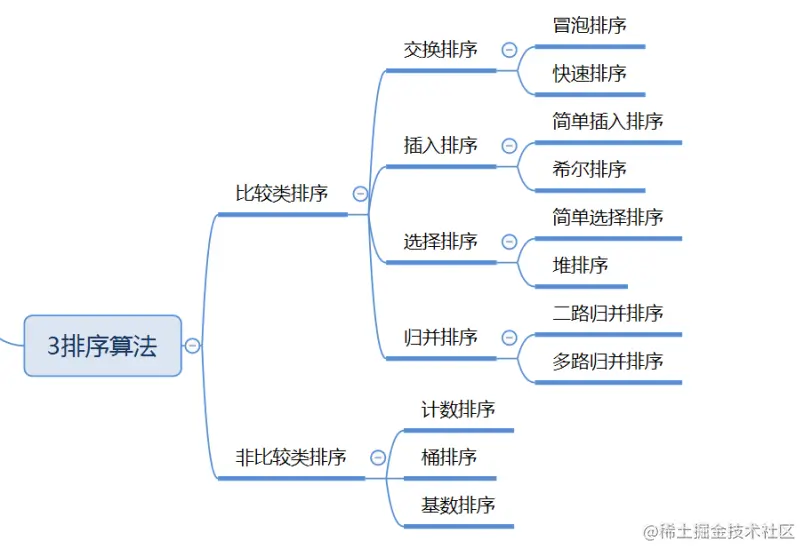
排序算法

选择排序算法

1,选择排序是一种简单直观的排序算法 

2,算法过程

   - 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，
   - 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
   - 以此类推，直到所有元素均排序完毕
3,算法效率,O: 是N的2次方

---

算法实现分解

分解1:从未被排序的数组中,找到最小的元素

int[] arrs = {8,6,1,7,2,5,4,12,9};
//遍历数组找到最小的元素的位置
int minValue = arrs[0]; //假设第一个元素是最小值
for(int i=0;i<arrs.length;i++) {
//判断当前位置的值是否比最小值
if(arrs[i] < minValue) {
//如果小，那么则取代原有的最小值
minValue = arrs[i];
    }
}
System.out.println("最小值是:"+minValue);

分解2:将最小值和未排序的数组的第一个元素互换

int[] arrs = {8,6,1,7,2,5,4,12,9};
//遍历数组找到最小的元素的位置
int minPosition = 0;
for(**int** i=0;i<arrs.length;i++) {
//判断当前位置的值是否比最小值
if(arrs[i] < arrs[minPosition]) {
//保存最小值所在的位置
minPosition = i;
    }
}
System.***out***.println("最小值是:"+arrs[minPosition]);
//实现交换
int temp = arrs[0];
arrs[0] = arrs[minPosition];
arrs[minPosition] = temp;
//输出交换后的结果
for (int i = 0; i < arrs.length; i++) {
System.out.print(arrs[i]+",");
}

分解3:将未排序的数组,分别执行分解1和分解2的操作,每次数组的起始位置都递增,直到排序完毕

int[] arrs = {8,6,1,7,2,5,4,12,9};
		//遍历数组找到最小的元素的位置
		int start = 0;//未排序的数组起始位置
		int minPosition = start;//设置最小元素为未排序元素首位
		for(int i=start;i<arrs.length;i++) {
			//判断当前位置的值是否比最小值
			if(arrs[i] < arrs[minPosition]) {
				//保存最小值所在的位置
				minPosition = i;
			}
		}
		System.out.println("最小值是:"+arrs[minPosition]);
		//实现交换
		int temp = arrs[start];
		arrs[start] = arrs[minPosition];
		arrs[minPosition] = temp;
		
		start = 1;
		minPosition = start;//设置最小元素为未排序元素首位
		for(int i=start;i<arrs.length;i++) {
			//判断当前位置的值是否比最小值
			if(arrs[i] < arrs[minPosition]) {
				//保存最小值所在的位置
				minPosition = i;
			}
		}
		System.out.println("最小值是:"+arrs[minPosition]);
		//实现交换
		temp = arrs[start];
		arrs[start] = arrs[minPosition];
		arrs[minPosition] = temp;
		
		start = 2;
		minPosition = start;//设置最小元素为未排序元素首位
		for(int i=start;i<arrs.length;i++) {
			//判断当前位置的值是否比最小值
			if(arrs[i] < arrs[minPosition]) {
				//保存最小值所在的位置
				minPosition = i;
			}
		}
		System.out.println("最小值是:"+arrs[minPosition]);
		//实现交换
		temp = arrs[start];
		arrs[start] = arrs[minPosition];
		arrs[minPosition] = temp;
		//输出交换后的结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i]+",");
		}

分解4:使用循环进行start的自增操作,并且循环执行分解1和分解2的操作

		int[] arrs = {8,6,1,7,2,5,4,12,9};
		//在最外层套一个循环，将start递增
		for (int start = 0; start < arrs.length; start++) {
			//遍历数组找到最小的元素的位置
			int minPosition = start;//设置最小元素为未排序元素首位
			for(int i=start;i<arrs.length;i++) {
				//判断当前位置的值是否比最小值
				if(arrs[i] < arrs[minPosition]) {
					//保存最小值所在的位置
					minPosition = i;
				}
			}
			System.out.println("最小值是:"+arrs[minPosition]);
			//实现交换
			int temp = arrs[start];
			arrs[start] = arrs[minPosition];
			arrs[minPosition] = temp;
		}
		
		//输出交换后的结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i]+",");
		}

冒泡排序

1,冒泡排序是一种简单的排序方法,它重复的走访过要排序的数列,一次比较两个元素,如果他们顺序错误就把他们交换过来

---

2,冒泡排序过程

    - 首先在未排序数组的首位开始，和后面相邻的数字进行比较，如果前面一个比后面一个大那么则进行交换。
    - 接下来在将第二个位置的数字和后面相邻的数字进行比较，如果大那么则进行交换，直到将最大的数字交换的数组的尾部。
    - 然后再从排序的数组的首位开始，重复前面两部将最大的数字交换到未排序数组的尾部（交换到尾部的数字是已经排好序)
    - 如此反复，直到排序完毕
3,这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的末端。

---

算法实现分解

分解1:将第一个数字和后面相邻的数字进行比较,如果大则进行交换

int[] arrs = {8,6,1,7,2,5,4,12,9};
		//判断大小
		if(arrs[0]>arrs[1]) {
			//如果大，则进行交换
			int temp = arrs[0];
			arrs[0] = arrs[1];
			arrs[1] = temp;
		}
		//输出结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i]+",");
		}

分解2:通过比较交换,将最大的数字交换到数组尾部

int[] arrs = { 8, 6, 1, 7, 2, 5, 4, 12, 9 };
		for (int i = 0; i < arrs.length - 1; i++) {
			// 判断大小
			if (arrs[i] > arrs[i + 1]) {
				// 如果大，则进行交换
				int temp = arrs[i];
				arrs[i] = arrs[i + 1];
				arrs[i + 1] = temp;
			}
		}
		// 输出结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i] + ",");
		}

分解3:重复执行分解1和分解2,将最大的数组换到未排序的数组尾部,直到排序结束

int[] arrs = { 8, 6, 1, 7, 2, 5, 4, 12, 9 };
		//////////////////////////
		//// 第一个轮交换，将数组中最大的数字交换到数组最后
		for (int i = 0; i < arrs.length - 1; i++) {
			// 判断大小
			if (arrs[i] > arrs[i + 1]) {
				// 如果大，则进行交换
				int temp = arrs[i];
				arrs[i] = arrs[i + 1];
				arrs[i + 1] = temp;
			}
		}
		//////////////////////////
		////第二个轮交换，将数组中最大的数字交换到数组倒数第二位置
		for (int i = 0; i < arrs.length - 2; i++) {
			// 判断大小
			if (arrs[i] > arrs[i + 1]) {
				// 如果大，则进行交换
				int temp = arrs[i];
				arrs[i] = arrs[i + 1];
				arrs[i + 1] = temp;
			}
		}
		//////////////////////////
		//// 第二个轮交换，将数组中最大的数字交换到数组倒数第三位置
		for (int i = 0; i < arrs.length - 3; i++) {
			// 判断大小
			if (arrs[i] > arrs[i + 1]) {
				// 如果大，则进行交换
				int temp = arrs[i];
				arrs[i] = arrs[i + 1];
				arrs[i + 1] = temp;
			}
		}
		// 输出结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i] + ",");
		}

分解4:利用循环代替重复操作

		int[] arrs = { 8, 6, 1, 7, 2, 5, 4, 12, 9 };
		for (int j = 1; j < arrs.length; j++) {
			//////////////////////////
			//// 第一个轮交换，将数组中最大的数字交换到数组最后
			for (int i = 0; i < arrs.length - j; i++) {
				// 判断大小
				if (arrs[i] > arrs[i + 1]) {
					// 如果大，则进行交换
					int temp = arrs[i];
					arrs[i] = arrs[i + 1];
					arrs[i + 1] = temp;
				}
			}
		}
		// 输出结果
		for (int i = 0; i < arrs.length; i++) {
			System.out.print(arrs[i] + ",");
		}