支持向量机
最大化间隔
原始代价函数
max∣∣w∣∣2 s.t. yi(wxi+b)≥1
约束条件表示所有样本都在两条线外
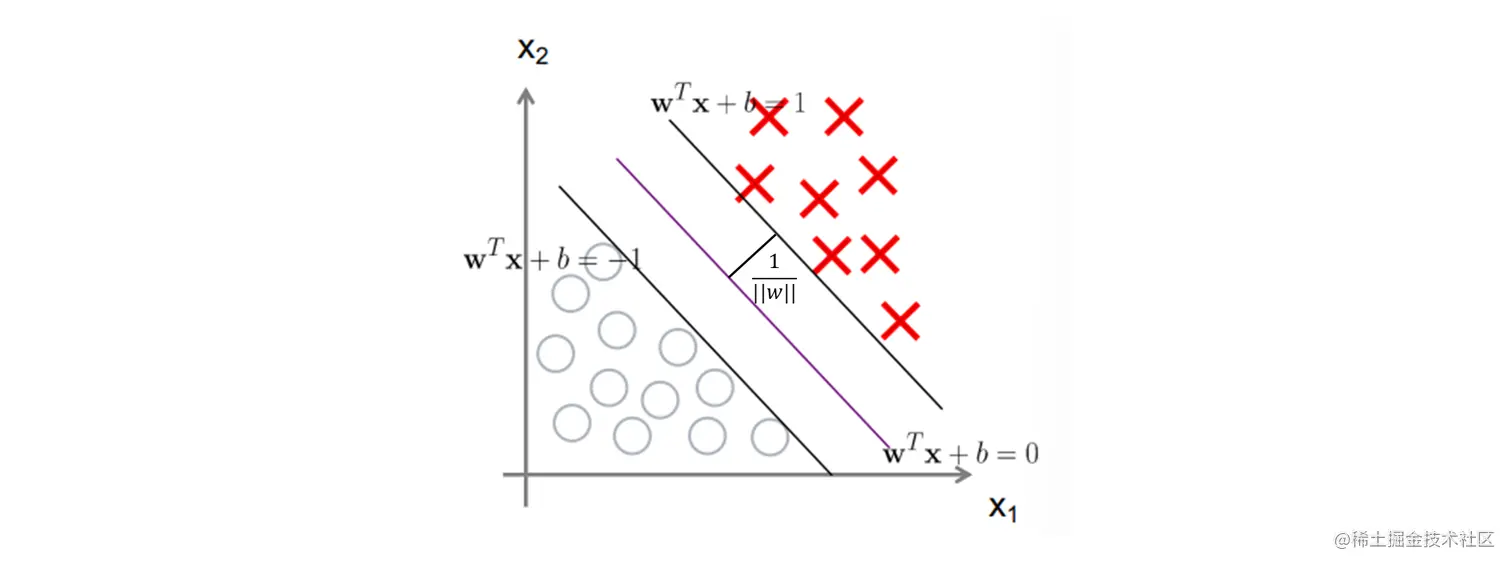
拉格朗日函数
要计算最大化间隔, 可以转成拉格朗日乘子法求极值
L=2∣∣w∣∣2+i=1∑mαi(1−yi(wxi+b))
其中 经验风险 为
i=1∑mαi(1−yi(wxi+b))
结构风险 为
2∣∣w∣∣2
经验风险用来度量预测模型与训练数据的误差, 结构风险用来避免 过拟合
判决函数
拉格朗日法求得模型参数 w 和 b 后得到判决函数
f(xi,w)={1−1wxi+b≥1wxi+b≤−1
SVM 优化
将拉格朗日函数转换成计算(称为原始代价函数的 最大最小对偶 )
αmax(w,bminL)
先对 w 和 b 求导
∂w∂L=w−i=1∑mαiyixi=0
∂b∂L=−i=1∑mαiyi=0
计算得到 w 代入拉格朗日函数中
w,bminL=21i=1∑mj=1∑mαiαjyiyjxixj−i=1∑mαiyi((j=1∑mαjyjxj)xi+b)+i=1∑mαi=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxixj
再利用拉格朗日乘子法求 α 极大 (又称为 αi 的 二次规划 )
αmaxL s.t. i=1∑mαiyi=0
计算得到 w 的最优解
w∗=i=1∑mαi∗yixi
再选择一个 αi∗>0 来计算 b∗
b∗=yi−i=1∑mαi∗yixixj
得到判决函数
f(x)=sign(wx+b)=sign(i=1∑mαiyixix+b)
软间隔
没办法完美的区分在两条线外时
max∣∣w∣∣2+Ci=1∑mξi s.t. yi(wxi+b)≥1−ξi
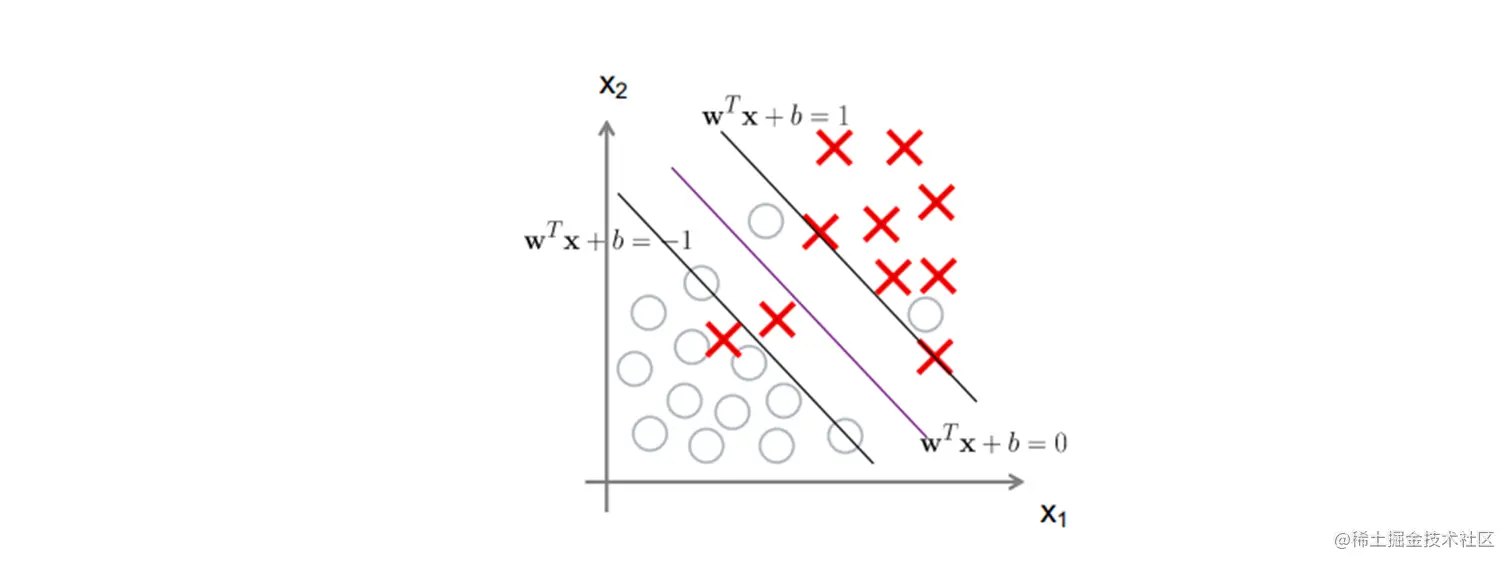
Hinge 损失
{ξi=1−yi(wxi+b)ξi≥0
当 yi=1 (正例) 时, wx+b≤1, 则 0≤1−yi(wx+b)≤1
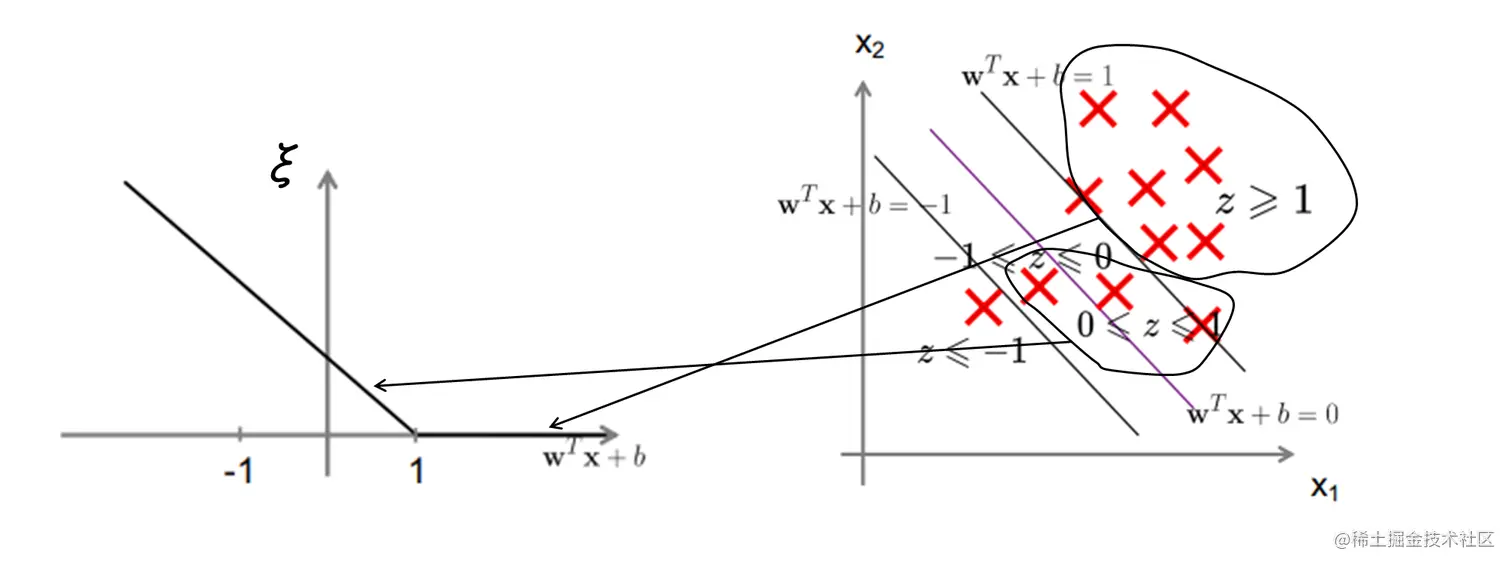
当 wx+b≥1 时, ξi=0 , 表示惩罚(误差)为 0
ξ=max(0,1−yi(wx+b))
拉格朗日函数
L=2∣∣w∣∣2+i=1∑mαi(1−yi(wxi+b))+Ci=1∑mξi−i=1∑mμiξi
代价函数
θminCi=1∑m[y(i)cost1(θx(i))+(1−y(i))cost0(θx(i))]+21i=1∑nθj2
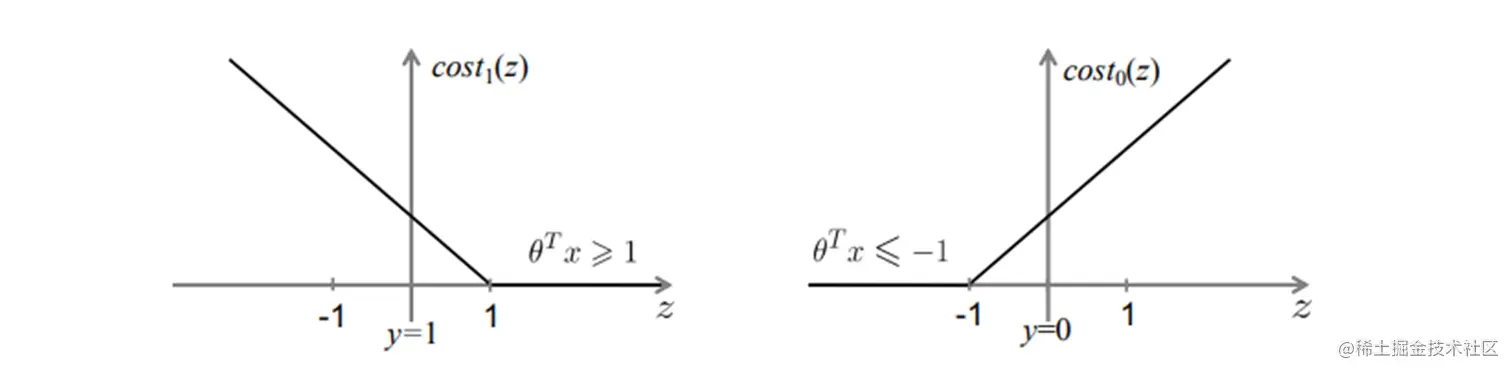
核函数
将非线性可分问题转变为 线性可分 问题
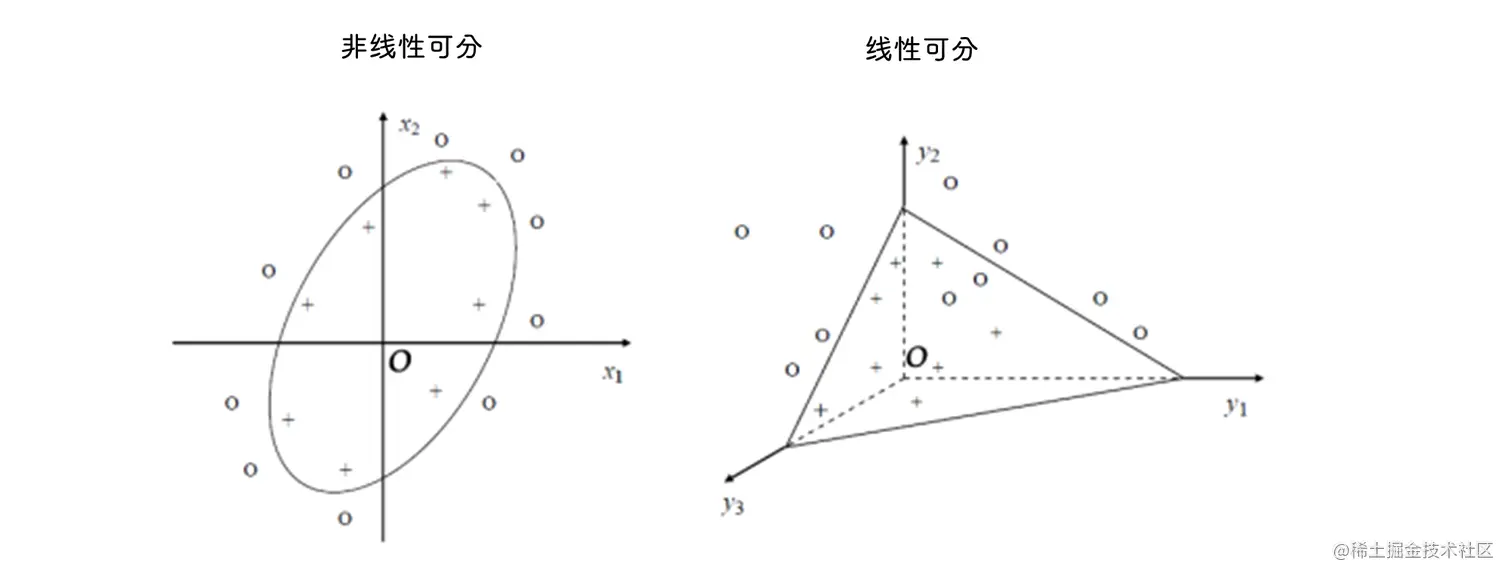
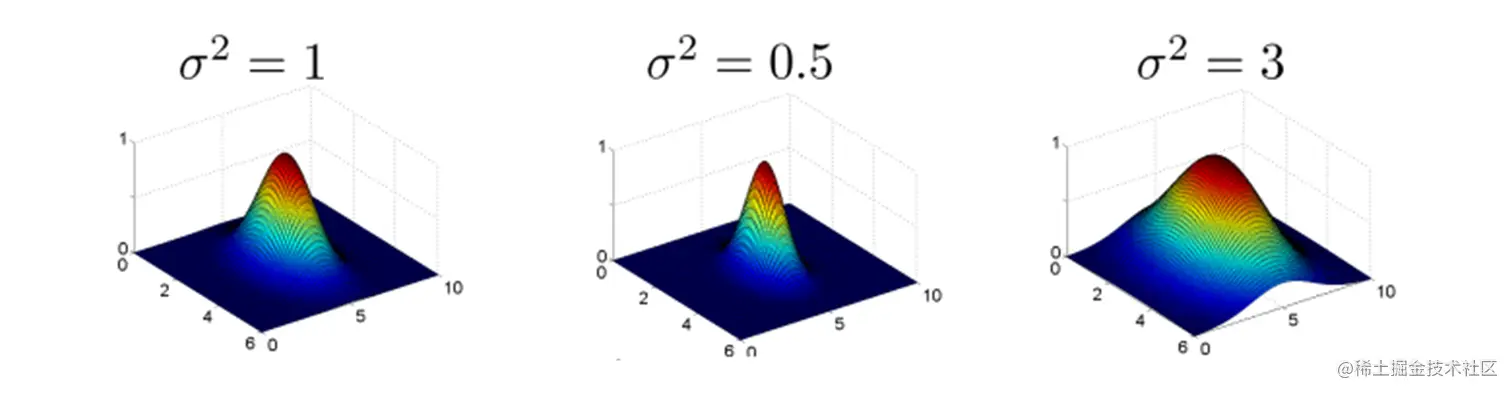
高斯径向基函数
K(x,y)=exp(2σ2−∣∣x−y∣∣2)=exp(−2σ2∑k=1n(xk−yk)2)
s = sum((x1 - x2).^2);
sim = exp(-s / 2 / sigma^2);
支持向量回归(SVR)
f(x) 与 y 的差异大于 e 时才计算损失
w,bmin21∣∣w∣∣2+Ci=1∑mmax(0,∣f(xi)−y∣−e)