索引介绍

索引是存储引擎用于快速定位到记录的一种存储结构，索引优化是针对大数据量查询性能优化的最有效的手段，合适的索引能够对查询性能提高几个数量级。也是程序员操作数据库最直接的优化方案。

但是索引也不是性能优化的“伸腿瞪眼丸”，不是说使用了索引就一定能够提高查询性能，相反如果不恰当的使用索引反而会影响整个表的性能。

索引是如何工作的？

索引的工作模式就跟我们平常看一本书，书前面的目录一样，找到我们关心的目录，然后根据页码直接定位到具体的位置。索引在数据库里面工作的模式也是如此，如果我们要查询一个我们关心的数据，去整个数据库表中搜索势必会很慢，而在我们针对这个数据建立的索引目录搜索，拿到了数据地址后就可以直接找到这个数据。

如：现在有一张表，表里面有一千万条记录，其中有个字段为account，每一行对应一个数据地址。

id account ...... 存储在磁盘上的物理地址
1 123456 ...... 0x1238983
2 322124 ...... 0x4231323
3 323222 ...... 0x4424343
..... ..... ......
10000000 232443 ..... 0x4343434

在没有建立索引的情况下，要查询最后一行account=232443这条记录，就等从头开始便利到尾，执行全表扫描一千万次，这样效率就非常低下。

如果我们对account建立了索引，比如B+索引，只需要两次磁盘IO就可以找到对应的物理地址；如果等值查询则hash索引只需要一次就可以找到对应的物理位置。因此根据数据和使用场景选择合适的索引是非常重要的，如果创建不符合要求的所有反而会带来额外的性能负担，如，我们要对account做法范围查询，但是建立了hash索引，这样就会导致索引失效，并且在插入和更新的时候要同时插入更新索引带来额外的开销。

id	account	......	存储在磁盘上的物理地址
1	123456	......	0x1238983
2	322124	......	0x4231323
3	323222	......	0x4424343
.....	.....	......
10000000	232443	.....	0x4343434

索引优点：

索引能大大减少数据库服务扫描的数据量
能够避免建立临时表
将随机的IO变为顺序IO

索引类型

MySQL中索引有很多种类型，为了适应不同业务场景查询需求，划分维度也不同。可以根据数据结构划分，物理存储角度划分，逻辑角度划分等。

数据结构划分

B-Tree（B+Tree)索引：B-Tree是数据库最常用的索引，B-Tree分为最开始的B-Tree和升级后的B+Tree。B-Tree的结构是一个N叉树结构，类似二叉搜索树。B-Tree在树上每个节点都有存储数据值，而B+Tree只有在叶子节点存储数据值并且有序的。

Hash索引：hash索引底层是一个Hash表，不存储具体的索引值，存储的是数据值得hash值与实际地址的映射关系。

物理存储划分

聚簇索引：聚簇索引是将数据和索引值存储在一起，找到了聚簇索引就找到了数据，使得数据与主键索引更加紧凑能够减少查询次数。普通索引存储的是主键索引（聚簇索引）的值。

非聚簇索引：非聚簇索引是将数据和索引分开存储，在存储模式上主键索引和普通所以与数据的关系是一样。

逻辑角度划分

普通索引：建立的单列索引，可以重复。

唯一索引：无能重复的普通索引。

主键索引：唯一索引+行记录唯一性标识索引，在使用聚簇索引存储的时候该索引会作为聚簇索引存在。

组合索引：多个列组成的索引。

全文索引：全文索引是一种特殊类型的索引，它查找的是文本中的关键词，而不是直接比较索引中的值。全文搜索和其他几类索引的匹配方式完全不一样。它有许多需要注意的细节，如停用词、词干和复数、布尔搜索等。全文索引更类似于搜索引擎傲的事情，而不是简单的WHERE 条件匹配。在相同的列上同时创建全文索引和基于值的B-Tree 索引不会有冲突，全文索引适用于MATCH AGAINST 操作，而不是普通的WHERE条件操作。

Hash索引

MySQL的Memory存储引擎是支持Hash索引的，但是像常用的InnoDB和MyISAM不支持该类型的。

Hash索引的存储结构：

Hash索引内部采用hash表，存储的对索引列计算的一个hash码，不会存储具体的数据。

如有以下数据：

id name age 地址（行号）
123 张三 16 0x1
345 李四 20 0x2
642 王五 19 0x3

现在对name列创建hash索引，创建过程中会对每个name进行一次hash计算得出hash的key也就是hash值。

hash(张三) = 2323、hash(李四) = 2458、hash(王五) = 7365（ps：示例数据，非真实数据）

hash表：

hash值地址（行号）
2323 0x1
2458 0x2
2323 0x3

注意：hash表的hash值是有顺序，从小到大，方便计算结果的时候进行索引。

此时要查询name=张三的行，则根据查询条件对张三做hash计算得出hash值为2323最后直接定位到行号为0x1的记录。

以上步骤是参考《高性能MySQL第3版》里面的。

这里我有一点疑问，就是真的有存储这个hash值吗，在书中有这样一句话注意每个槽的编号是顺序的，但是数据行不是。这句话的意思是编号有序是否就代表了每个hash槽的编号做了具体的存储，如果按照我们通常hash算法+数组的实现是不会存储这个hash槽的值，会直接用一个数组的下标作为hash值，数组值来直接保存具体的索引值地址，hash函数结算结果就是数组的下标。不过无论是否存储，至少hash查找是能够支持O(1)的查找的。

如果是有具体的存储hash值，即使hash值是有序的，那么我们在对索引值hash后查询的时候不也得在这个有序的hash表中查询具体的地址，这样就丢失了hash算法O(1)查找的时间复杂度。

id	name	age	地址（行号）
123	张三	16	0x1
345	李四	20	0x2
642	王五	19	0x3

hash值	地址（行号）
2323	0x1
2458	0x2
2323	0x3

Hash冲突：

MySQL处理hash冲突的时候也是按照经典的链表法处理的，即将发生了冲突的值用链表保存起来，因此如果发生了大量的hash冲突，查询速度肯定也是会退化的。

如上图所示：在一个足够长的数组中，张三和王五通过hash函数计算出来的hash值也就是数组下标都为2323，则此时它们会以链表的形式存储，如要查找王五的记录，第一步hash(王五)=2323，去下标2323的地方找，发现第一个是张三，然后不匹配继续往后找，再找到王五，从而得到了具体的存储地址0x3。因此如果hash冲突非常严重的情况下，就会形成一个非常长的链表，hash索引对其的查找就会退化成表冲突的索引值全部扫描。

具体hash算法的实现和优化可以参考以下Java里面的HashMap的实现。

hash索引的限制：

以下内容来自《高性能MySQL第3版》5.1.1索引类型-hash索引

哈希索引只包含哈希值和行指针，而不存储字段值，所以不能使用索引中的值来避免读取行。不过，访问内存中的行的速度很快，所以大部分情况下这一点对性能的影响井不明显。

哈希索引数据井不是按照索引值顺序存储的，所以也就无法用于排序。

哈希索引也不支持部分索引列匹配查找，因为哈希索引始终是使用索引列的全部内容来计算哈希值的。例如，在数据列（A,B ）上建立哈希索引，如果查询只有数据列A,则无撞使用该索引。

哈希索引只支持等值比较查询，包括＝、IN （）、＜＝＞（注意。和〈＝〉是不同的操作）。也不支持任何范围查询，例如WHERE price> 100。

访问哈希索引的数据非常快，除非有很多哈希冲突（不同的索引列值却有相同的哈希值）。当出现哈希冲突的时候，存储引擎必须遍历链表中所有的行指针，逐行进行比较，直到找到所有符合条件的行。

如果哈希冲突很多的话，一些索引维护操作的代价也会很高。例如，如果在某个选择性很低（哈希冲突很多）的列上建立哈希索引，那么当中删除一行时，存储引擎需要遍历对应哈希值的链表中的每一行，找到井删除对应行的引用，冲突越多，代价越大。

模拟hash索引

介绍Hash索引的时候有说道我们常用的InnoDB和MyISAM存储引擎都是不支持hash索引的，但是如果我们又想要使用hash算法来提高我们的查询等效率的话，就可以参考hash索引的实现，进行对使用这些存储引擎的数据模拟hash索引。

如：在《高性能MySQL第3版》中有一个例子非常适合这个场景。

当我们在数据库中存有url这种类型的长文本数据的时候，要对这类型的数据进行检索，我们可以有两种方案。

第一种方案就是对这个字段建立索引，一般都是B-Tree索引，但是这种方案会有个问题，因为一般的url这种长文本类型的数据，长度很难固定，而且一般都很长，如果对其建立B-Tree索引会占用很大的空间。

第二种方案就是对这个字段的数据增加其对应的hash值字段，然后对这个长文本检索的时候，检索前做一次hash计算，最后用计算出来的hash值与新增的hash字段的值进行索引，得到后再比较具体的值，这样性能会提升很多。

示例如下：

mysql> select * from ts_url;
+-----------------------+
| url                   |
+-----------------------+
| http://www.mysql.com  |
| http://www.baidu.com  |
| http://www.sougou.com |
+-----------------------+
3 rows in set (0.00 sec)

正常执行查询：mysql> SELECT id FROM ts_url where url = 'www.mysql.com';

在家了hash值后的数据

mysql> select * from ts_url;
+-----------------------+------------+
| url                   | url_crc    |
+-----------------------+------------+
| http://www.mysql.com  | 1560514994 |
| http://www.baidu.com  | 3500265894 |
| http://www.sougou.com | 2078973688 |
+-----------------------+------------+
3 rows in set (0.00 sec)

查询：mysql> SELECT * FROM ts_url where url_crc = CRC32(url) AND url = 'www.mysql.com'; 这样查询的效率会很高，因为我们对其的hash值建立索引。可能有人会好奇，我们查询条件中已经有了url_crc列的查询了为什么最后还是要加上url='xxx'的查询，这是因为通过CRC32函数计算出来的hash值会存在冲突，如果存在冲突的情况，就可以用后面的查询条件来保证结果的正确性。

B Tree

B Tree是Balance Tree的简称，中文称为多路平衡查找树。其中几个关键字多路、平衡、查找。在MySQL中分为B-Tree和B+Tree

多路：B树不像二叉树，只有左右节点，为了保证尽可能多存数据节点，降低树的高度，减少磁盘IO次数从而被设计成多路的树，每一个树节点都存储了多个子节点的引用。
平衡：B树是一个绝对平衡的的树，所有的叶子节点都在同一高度。
查找：B树的存储，在B树上每一个节点都代表了一个范围，其子节点能够能够根据都是基于这个范围创建，如上面根节点范围为10,20，那么它的左节点就小于范围的起始值，中间节点在范围内，右节点的值大于范围最大值，这样在查询的时候就能够很快索引。

简单步骤：

在上面图中，如果我们要查找15，则只需要在根节点通过二分查找或者其它算法找到其节点P1，然后进入P1就可以找到对应的值，经历两次IO。

实际步骤：

实际中B Tree中节点是以页为单位存储的，就是上面图中的page-x，每一页的大小默认为16KB，一次IO实际就是将一页加载到内存中，然后由该页里面的数据在内存中计算得出子节点页的位置再加载到内存中，从而得出结果。

B Tree的存储

一页能存多少数据呢？

MySQL的一页大小为16KB，可以通过show global status like 'innodb_page_size'; 语句来查看。也可以进行修改。

这里做个简单计算，16KB = 16384 B，如果我们存储int类型。

一个int类型数据占用4字节，一个指向下一页的指针为6字节，那么存储一个int类型数据节点则需要(4+6=10)字节的数据。

那么一页的16KB就可以存储16384/10=1638.4，舍去小数也是能存储1638个int类型节点的数据，这还只是一页的数量。

每一个int类型的节点又指向了一个子页，则高度为2的B Tree就可以存储 16381638 = 2683044 个节点，通常一颗B Tree的层数控制在3层，为了减少IO次数，则最终能够得到 16381638*1638 = 4394826072。一个三层，每页大小为16KB的B Tree可以存储43亿的int类型数据，当然这里只说了一颗B Tree只存储int类型数据，在数据库中实际存储的是一条记录，计算方式不能这样算。

也就是说即使我们在数据量达到了43亿的int数据里面检索一个值，也最多只需要两次IO即可。

MySQL具体的存储数据量估计在下面介绍完B+Tree的特性后有说明。

MySQL一页大小为什么要设置为16KB？

第一个原因是因为16KB正好是4KB的倍数，在操作系统中对磁盘的操作都是以页为基础单位操作的，这里的页是磁盘的单位，不是上面说的B Tree的节点页，一次IO操作根据文件系统的不同一次性会加载一页，而操作系统中一页正好为4KB，有的操作系统也会一次性加载多页，如1KB，4KB，8KB等；因此设置成16KB的原因它是4的倍数，这样能够保证每次IO都是一块完整的数据，避免因为造成多次IO，比如如果大小为17，则读取数据的时候就会多一次IO，并且多读的这个数据库所占数据比又很少，得不偿失。比如Oracle和SqlServer这些数据库的页大小都是8KB也是这个原因。

第二个原因也是考虑操作系统的特性，就是局部性原理，这里是大小设置，主要考虑到的是空间局部性原理。空间局部性原理指的是，一旦程序访问了某个存储单元，在不久之后，其附近的存储单元也将被访问，即程序在一段时间内所访问的地址，可能集中在一定的范围之内，这是因为指令通常是顺序存放、顺序执行的，数据也一般是以向量、数组、表等形式簇聚存储的。这也就是为什么数据紧凑存储，减少文件碎片会提高访问速度的原因。也就是说在操作系统一次性操作磁盘页大小为4KB的时候，直接将页大小设置为16KB也会将临近的页加载进内存，这样就减少了磁盘IO。

页大小也不是设置的越大越好，因为越大可能加载进内存的数据大多数是不需要的，造成了不必要的浪费，适量即可。

B-Tree

B-Tree的特点在于，它的每个节点里面都会存储索引所在行的指针。由于这个存储特性会造成两个重要问题：

数据查找的时候是一个相对不稳定的情况，比如我们要查找10和15这两条数据，那么10可以能就一次IO就能够找到，而15要两次IO，这个取决于数据的存储特性。
对扫表遍历效率低下，这个也是我认为为什么MyQL要用B+Tree来做索引的原因。对树这种数据结构熟悉的同学都知道，对一棵树要进行遍历是一件很麻烦的事情，像二叉树就分为了前序、中序、后序遍历，更别说这种n叉树的遍历，涉及到回溯等相关算法，会产生很多不必要的性能浪费。
数据指针冗余，我们看到对每一个字段的索引，它都得存储一个具体行的数据指针，如表字段有id、name建立了索引，则id索引树和name索引树里面都会存储大量的相同指针地址，这会导致什么问题呢，就是数据迁移的时候，需要修改所有的索引树上的数据指针。

可以看到，B Tree树是一个好树（好的数据结构），但是在我们实际数据库应用中，还存在不满足的缺陷，因此就有了应运而生的B+Tree，来解决这些问题。

B+Tree

InnoDB聚簇索引存储结构：

B+Tree相对于B-Tree的优化点：

从上面图中可以看到，B+Tree相对于B-Tree主要有两个优化，一是非叶子不存储数据，而是叶子结点是有序的并且用链表相互连接。这样就很好的解决了B-Tree留下的问题：

查询性能不稳定：在B+Tree中规定了只有叶子结点才存储数据，因此无论是查询一个多简单的值，都必须索引到叶子结点，IO次数=树的深度。

表扫描低下：由于所有数据都存在叶子节点，是以链表且有序存储的。数据就是天然的有序，而且链表是线性数据结构，因此在遍历和排序方面就能达到最高的性能。

数据指针冗余：这个在InnoDB中很好的解决了这个问题，因为它是聚簇索引，每个非主键索引都是存储的主键值，主键索引和数据存储在一起，因此无论怎么迁移数据，索引都是跟着数据走的，不存在批量修改数据地址的问题。这就相当于文件系统的相对路径和绝对路径存储。

并且B+Tree相对于B-Tree优化了上面的三个点外，还有就是由于其非叶子节点不存数据的特性，因此在相同的数据类型索引情况下，B+Tree可以比B-Tree存储更多的索引。

B+Tree的非叶子节点不存储数据，只有叶子节点存储数据，并且叶子节点之间是一个有序的链表。叶子节点存储的数据具体值，要分为主键索引和非主键索引和存储引擎的区别。

不同存储引擎对B+Tree的存储：

在InnoDB中，索引是使用的聚簇索引，即主键索引所在地址就是数据域所在。那么此时非主键索引存储的就是主键的值，如上面非主键索引所示。在查找数据的时候，主键索引找到了索引值就找到了数据行，而非主键索引找到了索引后还得根据存储的主键值去主键索引处找到数据，这种模式也称为回表。非主键索引就一定要产生回表嘛？ 这个不是一定的，在非主键索引中如果select选择的列都满足索引值，则用不着回表，如select id,name 如果id和name都是建立索引并用作了查询条件，则此时对于B+Tree来说找到了id和name的索引树值就已经满足了返回要求，没必要再去查询整个数据行了，也就不用回表了。

在MyISAM中，主键索引和非主键索引的数据区域存储的都是实际数据行的地址，因为MyISAM的索引和数据是分开存储的分别是.MYI文件和.MYD文件也就是说它并不会产生回表。

MyISAM存储结构：

B+Tree相对于B-Tree的优点？

我们可以看到B+Tree相对于B-Tree的改动主要在于两点：

一、非叶子节点不存储数据，所有数据存储在叶子节点，并固定树的高度。

非叶子节点不存储数据解决了B-Tree的查询不稳定问题，在相同索引的查询下它们的IO次数是相同的。并且使得数据存储更加聚集，极大的提高了索引的存储数量。

二、叶子节点之间用链表相连接，并保持有序。

用链表相连接叶子节点，也就相当于用链表连接了索引数据，而链表属于是线性数据结构，在元素遍历方面有着天然的优势，解决了B-Tree遍历树的劣势，同时维护了叶子节点为有序排列，这在范围查询有着很大的优势如between n and m，只要找到了起始点n就可以线性遍历到m取出数据。

InnoDB中B+Tree索引能存多少数据

操作系统的文件系统以页为基础存储单位，一页为4KB，MySQL中InnoDB的页大小为16KB；可以通过show variables like 'innodb_page_size';语句查看。

InnoDB的索引页既可以存放数据也可以存放索引，根据B+Tree的特性B+树中叶子节点存放数据，非叶子节点存放键值+指针。那么我们要计算实际存储的数据量，只需要计算聚簇索引中主索引的叶子节点数量即可。

假设我们数据库中一行记录占用空间大小为1KB，那么一页可以存储16条记录，聚簇索引的记录条数就等于叶子节点数量*16。

假设表中的索引为bigint，长度为8B，指针在InnoDB源码中为6B，则存储一个bigint类型的索引，需要占用8+6=14B。则一页16KB可以存储16384/14=1170 个索引。

现在得出，一页可以存储1170个索引值，可以存储16条数据。

则一颗高为2的树，1170*16=18720 条记录，1170为根节点存储的主索引，每条主索引都有一个指针指向一页数据，一页可存储16条数据。

那么用相同的算法，不难算出高位3层的B+Tree可以存储：1170117016=21902400条数据。结果也符合实际使用的数量级，千万级。

经历两次IO就可以从千万级数据中找出结果

参考：终极面试：InnoDB 中B+Tree索引树有多高，以及能存多少行数据？ | 码农网

扩展

为什么要选用B Tree作为索引的存储结构，用平衡二叉搜索树不行吗？

平衡二叉搜索树的定义为：节点的子节点高度差不能超过1,如上图中的节点20，左节点高度为1，右节点高度0，差为1，左子树所有节点小于根节点，右子树的所有节点大于根节点。它的搜索模式也是根据根节点索引左子树或者右子树，相对于线性存储也有着较高的搜索效率，但是为什么没有使用二叉树搜索树呢？

磁盘读写次数过多。在上面可以看到一颗7节点的二叉树，查询效率在最差的情况下要进行两次IO，二叉树决定了其指针只有左右子树，存储数据有限，如果再大量数据的情况下，会造成二叉树过高，造成多次磁盘IO，严重影响效率。

同样存在查询不稳定的情况，如上面查询10和查询3的IO次数完全不一样，如果采用B+Tree的叶子结点存储数据的形式，会极度的增加树的高度。

存储数据过少，上面说道了二叉树决定了它的局限性，只能有两个分支，能够存储的数据太少。而操作系统和磁盘交互是以页为单位，一页4KB加载进内存发现才一两个节点数据，极大的造成了浪费。

聚簇索引中存在的回表问题是否是设计缺陷？

我认为这不是缺陷，这是一种综合考虑后的结果。

前面介绍了聚簇索引和非聚簇索引的区别就在于，主索引是否跟数据存在一起，在InnoDB中由于只有主索引跟数据存储在一起，其它普通索引叶子结点存储了主索引的值，导致普通索引检索数据的时候，先检索到了普通索引后，还得去聚簇索引中根据主索引的值找到具体数据造成回表。而MyISAM的非聚簇索引中主索引和普通索引的叶子节点存储的都是数据的地址引用，找到了索引后就直接找到了数据，不会产生回表。

看似非聚簇索引查询效率要略高于聚簇索引一筹，但是这个也是相对而言的。

如果在频繁使用主索引查询的情况下聚簇索引理所当然效率更高，频繁使用普通索引查询的情况下MyISAM要更胜一筹（ps：这个只是根据原来分析出来的结果，实际谁快谁慢这个没有一定的）。

注意上面只说了查询，如果在频繁更新的情况下，InnoDB的聚簇索引就要高一大截了，比如现在有一条主键为1数据，对给数据建立了10个普通索引。如果这条数据存储地址发生了改变，在聚簇索引中只需要改变以下主索引对存储地址引用即可，而在非聚簇索引中则需要更新11个索引的叶子节点（1个主索引+10个普通索引）。

为了减少InnoDB的聚簇索引回表次数，MySQL退出了索引下推策略，借助非索引判断条件来减少回表次数

索引下推：

以前网上找的两种图，找不到出处了，借用一下：

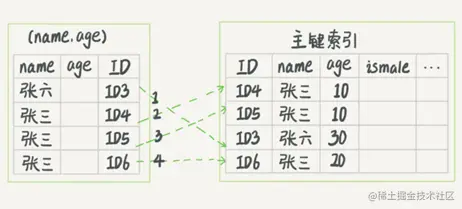
select * from user where name like '张%' AND age = 10;

当我们执行sql的时候，如果没有索引下推策略的时候，执行步骤为：

一、name索引树种找出主键值；二、去主索引上检索到数据；三、检索结果再根据 age=10进行过滤。回表次数为4。

有了索引下推策略：

一、name索引树种找出主键值；二、从过滤结果根据 age=10进行筛选；三、去主索引上检索到数据；回表次数为2。

从上面对比可以看到，所谓的索引下推就是在进行索引查找的同时提前判断是否可以进行where条件再过滤，缩小索引检索结果，减少回表次数。

MySQL索引原理总结