三角函数的加法定理及证明

hexu1985
1,457 阅读1分钟

三角函数的加法定理及证明

两个角α\alpha、β\beta的和或者差的三角函数，可以用α\alpha、β\beta角的三角函数的代数式来表示。

sin⁡(α+β)=sin⁡α⋅cos⁡β+cos⁡α⋅sin⁡β(1)\sin(\alpha + \beta) = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta \qquad\qquad (1)
sin⁡(α−β)=sin⁡α⋅cos⁡β−cos⁡α⋅sin⁡β(2)\sin(\alpha - \beta) = \sin \alpha \cdot \cos \beta - \cos \alpha \cdot \sin \beta \qquad\qquad (2)
cos⁡(α+β)=cos⁡α⋅cos⁡β−sin⁡α⋅sin⁡β(3)\cos(\alpha + \beta) = \cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta \qquad\qquad (3)
cos⁡(α−β)=cos⁡α⋅cos⁡β+sin⁡α⋅sin⁡β(4)\cos(\alpha - \beta) = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \qquad\qquad (4)
tan⁡(α+β)=tan⁡α+tan⁡β1−tan⁡α⋅tan⁡β(5)\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \cdot \tan \beta} \qquad\qquad (5)
tan⁡(α−β)=tan⁡α−tan⁡β1+tan⁡α⋅tan⁡β(6)\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \cdot \tan \beta} \qquad\qquad (6)

这一组公式也叫做三角函数的加法定理。还有叫“和差化积公式”或“和角公式（sum of angles formula）”的。

下面给出这组公式的证明，证明按照(4)→(3)→(1)→(2)→(5)→(6)(4) \rightarrow (3) \rightarrow (1) \rightarrow (2) \rightarrow (5) \rightarrow (6)的顺序给出。

证明：

我们首选证明公式(4)，证明思路是通过余弦定理和直角坐标系的两点间距离公式导出。

如下图：

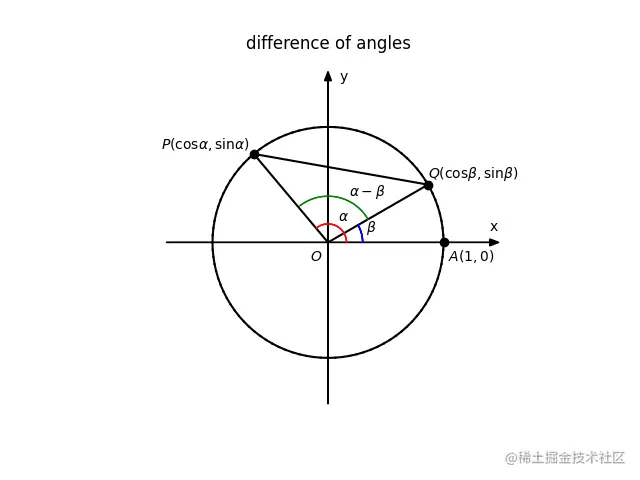
difference_of_angles.png

设PP、QQ是单位圆上的两点，∠AOP=α\angle AOP = \alpha，∠AOQ=β\angle AOQ = \beta，∠QOP=α−β\angle QOP = \alpha - \beta， 那么有，PP点的坐标为(cos⁡α,sin⁡α)(\cos \alpha, \sin \alpha)，QQ点的坐标为(cos⁡β,sin⁡β)(\cos \beta, \sin \beta)。 根据余弦定理有

∣PQ∣2=∣OP∣2+∣OQ∣2−2∣OP∣⋅∣OQ∣cos⁡(α−β)(7)|PQ|^{2} = |OP|^{2} + |OQ|^{2} - 2|OP| \cdot |OQ| \cos (\alpha - \beta) \qquad\qquad (7)

其中∣OP∣=∣OQ∣=1|OP| = |OQ| = 1，所以(7)式可以化简为

∣PQ∣2=2−2cos⁡(α−β)(8)|PQ|^{2} = 2 - 2 \cos (\alpha - \beta) \qquad\qquad (8)

再根据两点间的距离公式有

∣PQ∣=(cos⁡α−cos⁡β)2+(sin⁡α−sin⁡β)2(9)|PQ| = \sqrt{(\cos \alpha - \cos \beta)^{2} + (\sin \alpha - \sin \beta)^{2}} \qquad\qquad (9)

将(9)式两边取完全平方并化简

∣PQ∣2=(cos⁡α−cos⁡β)2+(sin⁡α−sin⁡β)2=cos⁡2α−2cos⁡α⋅cos⁡β+cos⁡2β+sin⁡2α−2sin⁡α⋅sin⁡β+sin⁡2β=2−2(cos⁡α⋅cos⁡β+sin⁡α⋅sin⁡β)(10)\begin{aligned} |PQ|^{2} & = (\cos \alpha - \cos \beta)^{2} + (\sin \alpha - \sin \beta)^{2} \\ & = \cos ^{2} \alpha - 2 \cos \alpha \cdot \cos \beta + \cos ^{2} \beta + \sin ^{2} \alpha - 2 \sin \alpha \cdot \sin \beta + \sin ^{2} \beta \\ & = 2 - 2 (\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta) \qquad\qquad (10) \end{aligned}

将(8)式代入(10)式，并化简就有

cos⁡(α−β)=(cos⁡α⋅cos⁡β+sin⁡α⋅sin⁡β)\cos (\alpha - \beta) = (\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta)

公式(4)得证。

通过(4)式，将β\beta换成−β-\beta，加上诱导公式可得出公式(3)

cos⁡(α+β)=cos⁡(α−(−β))=cos⁡α⋅cos⁡(−β)+sin⁡α⋅sin⁡(−β)=cos⁡α⋅cos⁡β−sin⁡α⋅sin⁡β\begin{aligned} \cos (\alpha + \beta) & = \cos (\alpha - (-\beta)) \\ & = \cos \alpha \cdot \cos (-\beta) + \sin \alpha \cdot \sin (-\beta) \\ & = \cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta \end{aligned}

同样的方式可以证明公式(1)

sin⁡(α+β)=cos⁡(π2−(α+β))=cos⁡((π2−α)−β)=cos⁡(π2−α)⋅cos⁡β+sin⁡(π2−α)⋅sin⁡β=sin⁡α⋅cos⁡β+cos⁡α⋅sin⁡β\begin{aligned} \sin(\alpha + \beta) & = \cos(\frac{\pi}{2} - (\alpha + \beta)) \\ & = \cos((\frac{\pi}{2} - \alpha) - \beta) \\ & = \cos(\frac{\pi}{2} - \alpha) \cdot \cos \beta + \sin(\frac{\pi}{2} - \alpha) \cdot \sin \beta \\ & = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta \end{aligned}

然后由公式(1)推出公式(2)

sin⁡(α−β)=sin⁡(α−(−β))=sin⁡α⋅cos⁡(−β)+cos⁡α⋅sin⁡(−β)=sin⁡α⋅cos⁡β−cos⁡α⋅sin⁡β\begin{aligned} \sin(\alpha - \beta) & = \sin (\alpha - (-\beta)) \\ & = \sin \alpha \cdot \cos (-\beta) + \cos \alpha \cdot \sin (-\beta) \\ & = \sin \alpha \cdot \cos \beta - \cos \alpha \cdot \sin \beta \end{aligned}

由公式(1)和公式(3)推出公式(5)

tan⁡(α+β)=sin⁡(α+β)cos⁡(α+β)=sin⁡α⋅cos⁡β+cos⁡α⋅sin⁡βcos⁡α⋅cos⁡β−sin⁡α⋅sin⁡β=(sin⁡α⋅cos⁡β+cos⁡α⋅sin⁡β)/(cos⁡α⋅cos⁡β)(cos⁡α⋅cos⁡β−sin⁡α⋅sin⁡β)/(cos⁡α⋅cos⁡β)=tan⁡α+tan⁡β1−tan⁡α⋅tan⁡β\begin{aligned} \tan(\alpha + \beta) & = \frac{\sin(\alpha + \beta)}{\cos (\alpha + \beta)} \\ & = \frac{\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta}{\cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta} \\ & = \frac{(\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta)/(\cos \alpha \cdot \cos \beta)}{(\cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta)/(\cos \alpha \cdot \cos \beta)} \\ & = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \cdot \tan \beta} \end{aligned}

同样的方式，由公式(2)和公式(4)推出公式(5)

tan⁡(α−β)=sin⁡(α−β)cos⁡(α−β)=sin⁡α⋅cos⁡β−cos⁡α⋅sin⁡βcos⁡α⋅cos⁡β+sin⁡α⋅sin⁡β=(sin⁡α⋅cos⁡β−cos⁡α⋅sin⁡β)/(cos⁡α⋅cos⁡β)(cos⁡α⋅cos⁡β+sin⁡α⋅sin⁡β)/(cos⁡α⋅cos⁡β)=tan⁡α−tan⁡β1+tan⁡α⋅tan⁡β\begin{aligned} \tan(\alpha - \beta) & = \frac{\sin(\alpha - \beta)}{\cos (\alpha - \beta)} \\ & = \frac{\sin \alpha \cdot \cos \beta - \cos \alpha \cdot \sin \beta}{\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta} \\ & = \frac{(\sin \alpha \cdot \cos \beta - \cos \alpha \cdot \sin \beta)/(\cos \alpha \cdot \cos \beta)}{(\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta)/(\cos \alpha \cdot \cos \beta)} \\ & = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \cdot \tan \beta} \end{aligned}

至此，加法定理的6个公式证明完毕。■\blacksquare

avatar
文章
阅读
粉丝