详解决策树-CART算法【十分钟机器学习系列笔记】

持续创作，加速成长！这是我参与「掘金日新计划 · 10 月更文挑战」的第20天，点击查看活动详情

视频作者：简博士 - 知乎 (zhihu.com)；简博士的个人空间_哔哩哔哩_bilibili

链接：【合集】十分钟 机器学习 系列视频 《统计学习方法》_哔哩哔哩_bilibili

原书：《统计学习方法》李航

 

基尼指数

ID3算法通过信息增益求特征、C4.5通过信息增益比求特征，而在CART算法中，是通过基尼指数来选择最优特征的。

 

假设有$K$个类，样本点属于第$k$类的概率为$p_{k}$，概率分布的基尼指数定义为

显然，这就是样本点被错分的概率期望并进行加权，权重为$p_{k}$。

 

对于二分类问题来说，如果样本点属于第一类的概率是$p$，那么第二类的概率就行$1-p$，代入到基尼指数为

如果对给定的样本集合$D$，可以分为两个子集$C_{1}$和$C_{2}$

其中，$C_{k}$表示$k$类样本的个数，$\begin{aligned} \frac{|C_{1}|}{|D|}\end{aligned}$就是$p$的经验值

CART算法生成二叉决策树是通过基尼指数挑选特征，但其实基尼指数可以用到多分类问题中

如果给定的样本集合$D$，可以分为$K$个子集：$C_{1},C_{2},\cdots ,C_{K}$，其基尼指数

其中，$\begin{aligned} \frac{|C_{k}|}{|D|}\end{aligned}$就是$p_{k}$的经验值

 

对于特征$A$条件下，样本集$D$的基尼指数为

这里就是选定了特征$A$，并且将数据集中按照特征分成了两个数据集，再分别求它们对应的基尼指数

 

例：用基尼指数的最小化来选出最优特征

设有10个水蜜桃，其中5个好吃，5个不好吃，那么我们可以计算整个数据集的基尼指数

假设，甜度大于0.2的有6个桃子，其中5个好吃，1个不好吃，甜度小于等于0.2的有4个桃子，都不好吃

分别计算$D_{1},D_{2}$的基尼指数

计算甜度特征下的基尼指数

假设，有5个硬桃子，其中2个好吃，3个不好吃，5个软桃子中，有3个好吃，2个不好吃。

 

分别计算$D_{1},D_{2}$的基尼指数

计算甜度特征下的基尼指数

通过比较可以看出

因此按照甜度分类时，我们选择硬度作为根节点

 

CART分类算法

如果输出变量是离散的，对应的就是分类问题；如果输出变量是连续的，对应的就是回归问题

 

分类树算法

输入：数据集$D$，特征集$A$，停止条件阈值$\epsilon$

输出：分类决策树

1. 从根节点出发，构建二叉树。

2. 计算现有特征下对数据集$D$基尼指数，选择最优特征

    - 在特征$A_{g}$下，对其可能取的每个值$a_{g}$，根据样本点对$A_{g}=a_{g}$的测试为“是”或“否”，将$D$分割成$D_{1}$和$D_{2}$两部分，计算$A_{g}=a_{g}$时的基尼指数

    - 选择基尼指数最小的那个值作为该特征下的最优切分点

    - 计算每个特征下的最优切分点，并比较在最优切分下每个特征的基尼指数，选择基尼指数最小的那个特征，即最优特征

3. 根据最优特征与最优切分点，从现结点生成两个子结点，将训练集依照特征分配到两个子结点中去

4. 分别对两个子结点递归地调用上述步骤，直至满足停止条件（比如结点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值（样本基本属于同一类），或者密友更多特征），即生成CART决策树

 

例：利用CART构建分类树

 

 

训练集$D$，特征集分别是$A_{1}$年龄，$A_{2}$是否有工作，$A_{3}$是否有自己的房子，$A_{4}$信贷情况。类别为$y_{1}=$是，$y_{2}=$否

先用基尼指数的最小化选出最优特征

 

选择年龄$A_{1}$这个特征，由于有三个分类，根据CART算法规定，我们需要将其改为二分类

设青年$A_{11}$，中年$A_{12}$，老年$A_{13}$

 

划为青年和非青年，计算基尼指数

同理以中年和非中年分类，以老年和非老年分列

青年和老年基尼指数最小，都可以作为最优划分点，我们选择青年

 

选择工作$A_{2}$这个特征

设有工作$A_{21}$，无工作$A_{22}$

 

计算基尼指数

 

选择房子$A_{3}$这个特征

设有房子$A_{31}$，无房子$A_{32}$

 

计算基尼指数

 

选择信贷情况$A_{4}$这个特征

设非常好$A_{41}$，好$A_{42}$，一般$A_{43}$三个特征值

 

计算基尼指数

一般的基尼指数最小，作为最优划分点

 

对比四个特征得到的基尼指数

 

特征值	基尼指数
年龄	0.44
工作	0.32
房子	0.27
信贷情况	0.32

 

因此我们选择房子，绘制二叉树

 

 

 

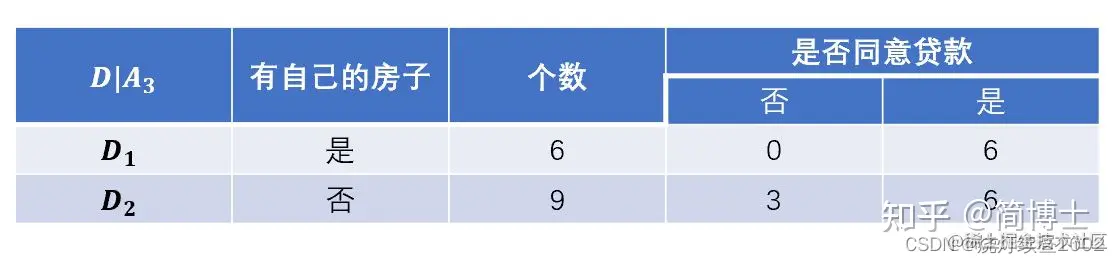
可以发现有房子的都同意贷款，因此这是一个叶结点。继续对无房子的数据集进行统计，按照年龄。工作、信贷情况来分类

 

在无房子数据集内，以年龄特征分类

 

年龄	个数	不同意贷款	同意贷款
青年	4	3	1
中年	2	2	0
老年	3	1	2

 

在无房子数据集内，以工作特征分类

 

工作	个数	不同意贷款	同意贷款
有工作	3	0	3
无工作	6	6	0

 

在无房子数据集内，以信贷情况特征分类

 

信贷情况	个数	不同意贷款	同意贷款
非常好	1	0	1
好	4	2	2
一般	4	4	0

 

显然房子作为特征的基尼指数为$0$，因此我们可以由房子继续构建二叉树

 

 

回归树算法

由于是有监督的回归模型，因此我们应当对输入数据集进行划分，而不是划分输出

 

假设将输入空间划分成$M$个单元，$R_{1},R_{2},\cdots ,R_{M}$，并在每个单元$R_{m}$上有一个固定的输出值$c_{m}$，回归树模型可以表示为

这里的$f(x)$就是CART回归树模型，$c_{m}$代表输出的类，$I(x \in R_{m})$就是指示性函数

我们通过平方误差最小化来找到最优切分点。选择第$x^{(j)}$个变量和取值$s$，分别作为切分变量和切分点，并定义两个区域

最小化平方误差就可以表示为

这个公式意味着，将输出变量按照输入变量分为了两类，然后要求出来每次分类后的各个分类的平方误差最小值之和，也就意味着整体的最小平方误差，平方误差最小，意味着分类和实际最吻合。其中

$\hat{c_{i}}$就是每个区域输出变量的平均值

 

该算法停止可以认为划分到合适就停止，也可以整个都划分完，没有多余的点

 

例：利用CART构建回归树。$甜度 \in (0,1),好吃程度\in (0,10)$

 

甜度	0.05	0.15	0.25	0.35	0.45
好吃程度	5.5	7.6	9.5	9.7	8.2

 

我们指定甜度为输入，好吃程度为输出

以甜度$s=0.1$进行划分

可以将表格里的连续数据划分为$R_{1}$和$R_{2}$两类

$R_{1}$类是

 

甜度	0.05
好吃程度	5.5

 

$R_{2}$类是

 

甜度	0.05	0.15	0.25	0.35	0.45
好吃程度	5.5	7.6	9.5	9.7	8.2

 

可得

 

以甜度$s=0.2$进行划分，平方误差和为$3.53$

以甜度$s=0.3$进行划分，平方误差和为$9.13$

以甜度$s=0.4$进行划分，平方误差和为$11.52$

 

因此我们选定$s=0.1$作为最优划分点，同时输出模型为

当然我们还可以对$s>0.1$区域进行回归划分，这就要取决于你的停止条件，如果说是继续分成三类，那么就可以按照相同的思路进行计算。

通过对连续变量进行划分，就可以转换为离散的变量来进行计算，那么就和之前的分类树模型也是相通的方法

 

剪枝算法

根据剪枝前后的损失函数来决定是否剪枝，剪枝后，如果损失函数减小，则意味着可以剪枝。

$C(T)$反映的是代价，是对训练数据的预测误差（比如基尼指数、平方误差），也就是模型的拟合能力；$|T|$反映的是模型的复杂度，体现的是泛化能力，$|T|$表示子树上叶结点的概述，叶结点越多，模型越复杂

$\alpha$是一个决定拟合和泛化综合效果的参数

• 当$\alpha=0$时，损失函数仅由拟合决定，不考虑对未知数据的预测能力，所以这样得到的是一棵最完整的决策树，泛化能力弱

• 当$\alpha=+\infty$时，得到的是单结点树，对于任何数据的泛化能力都很强，但拟合效果差

 

显然$\alpha$的选取决定了整个决策树的样子

 

$\alpha$可以从$0$取到$+\infty$，我们将这个区间分成多个小区间，即

这时，令每一个$\alpha$仅对应着一棵决策树。接着，我们把这些$\alpha$按照左闭右开的形式划成小区间，即

总共有$n$个区间，每个小区间都对应着一个决策树，我们记作

这里$T_{0}$就代表着$\alpha=0$时完整的决策树，意味着没有剪枝。然而我们要找的是最优的决策树，其对应的$\alpha_{i}$使得损失函数$C_{\alpha}(T_{i})$最小

 

假设我们有一棵子树，叫做$T_{t}$，那么剪枝前的损失函数可以写成

剪枝后变成一个叶结点，也就意味着此时$|T|=1$，那么损失函数可以写成

当$\alpha$充分小，甚至$\alpha=0$时，显然有

当$\alpha$充分大，甚至$\alpha \to +\infty$时，显然有

因此在$[0,+\infty)$之间一定存在一个$\alpha$，使得

在该$\alpha$情况下，可得

 

这里我们要先明确一点

Breiman等人证明：可以用递归的方法对树进行剪枝，将α从小到大排列，$0=α0<α1<⋯<αn<+∞$，产生一系列的区间，剪枝得到的子树序列对应着区间$α∈[αi,αi+1)，i=0,1,...,n$的最优子树序列$\{T_0,T_1,T_2,...,T_n\}$,序列中的子树是嵌套的（即$T_1$是$T_0$的子树、$T_2$是$T_1$的子树）。

作者：猎人yy

链接：机器学习篇：（一）决策树_猎人yy的博客-CSDN博客

有说李航书中有写，但我好像看漏了……

这也告诉我们，每次一定可以只减一个结点，因为上面的$\alpha$大于等于下面的$\alpha$

这里有个疑问，根据这个原理，是否我们只需要计算每一个枝条最下面的叶结点的$\alpha$，然后对比，谁小剪谁

实际上这个$g(t)$表示剪枝的阈值，即对于某一结点$\alpha$，当总体损失函数中的参数$\alpha= g(t)$时，剪和不剪总体损失函数是一样的（这可以在书中（5.27）和（5.28）联立得到）。这时如果$\alpha$稍稍增大，那么不剪的整体损失函数就大于剪去的。即$\alpha$大于$g(t)$该剪，剪了会使整体损失函数减小；$\alpha$小于$g(t)$不该剪，剪了会使整体损失函数增大。

（请注意上文中的总体损失函数，对象可以是以$\alpha$为根的子树，也可以是整个CART树，对$\alpha$剪枝前后二者的总体损失函数增减是相同的。）

对于同一棵树的结点，$\alpha$都是一样的，当$\alpha$从0开始缓慢增大，总会有某棵子树该剪，其他子树不该剪的情况，即$\alpha$超过了某个结点的$g(t)$，但还没有超过其他结点的$g(t)$。这样随着$\alpha$不断增大，不断地剪枝，就得到了$n+1$棵子树，接下来只要用独立数据集测试这$n+1$棵子树，试试哪棵子树的误差最小就知道那棵是最好的方案了。

作者：Zergzzlun - 知乎 (zhihu.com)

链接：cart树怎么进行剪枝？ - 知乎 (zhihu.com)

因此对于CART算法生成的一个很大的决策树，其剪枝只是剪出了$n+1$个子树，告诉我们应该如果要剪枝，那么剪枝的顺序应该是什么，即从1到n+1

 

步骤

输入：CART算法生成的完整决策树

输出：最优决策树$T_{\alpha}$

1. 设$k=0,T=T_{0}$也就是从完整的决策树出发

    $k$表示迭代次数，这里从$0$开始，也就意味着还没开始迭代，那么树也是完整的，从这里开始出发。

2. 设$\alpha=+\infty$，因为后面我们要比较大小，当损失函数小的时候可以剪枝。

3. 自下而上的对各个内部结点$t$计算$C(T_{t}),|T_{t}|$，以及

    $g(t)=\frac{C(t)-C(T_{t})}{|T_{t}|-1},\alpha=\min (\alpha,g(t))$

    这里$g(t)$代表了在这个结点对应的$\alpha$值；$C(t)$代表了单结点时的误差；$C(T_{t})$代表了子树时的误差

   

    注意：此处的预测误差与我们之前所介绍的预测错误率不同，它还可以包括平方损失、基尼指数等。为了简便，后面例题中，我们还是以预测错误率来计算。

4. 自下而上的方位内部结点$t$，如果有$g(t)=\alpha$，则进行剪枝，并对叶结点$t$以多数表决法决定类，得到数$T$

5. 接着增加迭代次数，继续调用，最终采用交叉验证法在子树$T_{0},T_1,T_{2},\cdots ,T_{n}$中选取最优子树$T_{\alpha}$

 

例题

 

 

设$k=0,T=T_{0}$，从完整的决策树开始，设置$\alpha=+\infty$，又有

因为内部节点有三个，我们可以把$T_{0},T_{1},T_{2}$分别对应$t=0,t=1,t=2$，对于$C(t)$代表了单结点时的预测误差，这里因为我们选用的是预测错误率来计算

 

第一次迭代

对于$T_{0}$子树而言，一共有17个样本点，其中8个正类，9个负类，如果按照多数表决来设置单结点的话，那么应该设为负类，这样误判的个数就为8，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{0})$，可以看出在$T_{0}$子树中，对应的6个叶子结点里，只有从左数第2个结点有1个误判。 因此

代入计算

取

对于$T_{1}$子树而言，一共有9个样本点，其中7个正类，2个负类，如果按照多数表决来设置单结点的话，那么应该设为正类，这样误判的个数就为2，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{1})$，可以看出在$T_{1}$子树中，没有误判。因此

代入计算

取

对于$T_{2}$子树而言，一共有8个样本点，其中7个正类，1个负类，如果按照多数表决来设置单结点的话，那么应该设为负类，这样误判的个数就为1，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{2})$，可以看出在$T_{2}$子树中，对应的2个叶结点中，没有误判，因此

代入计算

取

可以看出，$g(2)=g(1)=\alpha=\frac{1}{17}$，因此不妨对内部节点$T_{2}$子树剪枝

 

 

第二次迭代

对于$T_{0}$子树而言，一共有17个样本点，其中8个正类，9个负类，如果按照多数表决来设置单结点的话，那么应该设为负类，这样误判的个数就为8，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{1})$，这里就发生了一些不一样，可以看出在$T_{0}$子树中，对应的三个叶结点里，对于$T_{1}$结点而言，由于这里拿正类结点替代，那么误判个数就变成了2个，因此：

代入计算

取

注意：在第二次迭代中，此时的$\alpha$是第一轮中的结果，也就是$\frac{1}{17}$

对于$T_{0}$子树而言，一共有9个样本点，其中7个正类，2个负类，如果按照多数表决来设置单结点的话，那么应该设为正类，这样误判的个数就为2，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{1})$，可以看出在$T_{1}$子树中，由于第一个叶结点属于正类，误判了1个。 因此：

 

个人理解，这里也是加权过的，即

$C(T_{1})=\frac{9}{17}\times \frac{1}{9}=\frac{1}{17}$

 

代入计算

取

可以看出，这里的$T_{1}$子树对应的$\alpha$是最小值，意味着对$T_{1}$剪枝

 

 

第三次迭代

对于$T_{0}$子树而言，一共有17个样本点，其中8个正类，9个负类，如果按照多数表决来设置单结点的话，那么应该设为负类，这样误判的个数就为8，同时还要乘以这棵子树中样本点占总体的权重。 因此

接着求$C(T_{1})$，这里就发生了一些不一样，可以看出在$T_{0}$子树中，对应的两个叶结点里，对于$T_{1}$结点而言，由于这里拿正类结点替代，那么误判个数就变成了3个，因此：

代入计算

取

$T_{0}$子树对应的不是最小$\alpha$，因此不剪枝，同时根节点满足两个叶结点的停止条件，剪枝结束