---

本文从两方面进行解释：数学和编码方面。总有一个角度能让你更好理解。

数学解释

熵 Entropy

熵用于计算一个离散随机变量的信息量。对于一个概率分布$X$，$X$的熵就是它的不确定性。 用大白话来说，假设你预测一个东西，有时候结果会出乎意料，熵就表示出乎意料的程度。熵越大你越不容易预测对，事情就越容易出乎意料。

离散型概率分布$X$的熵定义为自信息的平均值：

注意： 熵的单位可以是比特（bits）也可以是奈特（nats）。二者区别在于前者是用$\log_2$计算，后者是用$\log_e$计算。我们这里是用$\log_2$计算。

举个栗子算一下熵。

两个城市明天的天气状况如下：

现在有两个事件：

• A市明天的天气状况
• B市明天的天气状况

$H(A)=-0.8 \times \log 0.8-0.15 \times \log 0.15-0.05 \times \log 0.05=0.884$

$H(B)=-0.4 \times \log 0.4-0.3 \times \log 0.3-0.3 \times \log 0.3=1.571$

可以看到B的熵比A大，因此B城市的天气具有更大的不确定性。

交叉熵 Cross-Entropy

交叉熵用于度量两个概率分布间的差异性信息。 再用大白话说一下，比如你认为一件事有六成概率能成功，实际上你去做的时候你又八成概率能成功。这时候结果出乎意料的程度就是交叉熵。

交叉熵的数学定义：

举个栗子算一下交叉熵。

改了一下表头。 现在还是有两个事件：

• $P$实际A城市明天的天气状况
• $Q$你以为的A城市的天气状况

$H(P,Q)=-0.8 \times \log0.4-0.15 \times \log0.3 - 0.05 \times \log 0.3 = 1.405$

KL散度 Kullback-Leibler divergence

KL散度又称相对熵、信息增益，相对于交叉熵来说，是从另一个角度计算两个分布的差异程度。相对于分布X，分布Y有多大的不同？这个不同的程度就是KL散度。

注意，KL散度是不对称的，也就是说X关于Y的KL散度 不等于 Y关于X的KL散度。

若 $A$ 和 $B$ 为定义在同一概率空间的两个概率测度，定义 $A$ 相对于 $B$ 的相对熵为

举个栗子算一下KL散度。

还是用这个例子：

现在还是有两个事件：

• $P$实际A城市明天的天气状况
• $Q$你以为的A城市的天气状况

$D(P \|Q) = 0.8 \times \log(0.8 \div0.4) + 0.15 \times \log(0.15 \div 0.3) + 0.05 \times \log(0.0.5\div 0.3) =0.521$

熵、KL散度和交叉熵的关系

我们从上边三个例子中可以看到：

• A城市明天实际天气状况的熵$H(A)=0.884$
• A城市明天实际天气状况和你预测的天气状况的交叉熵为$H(P,Q)=1.405$
• A城市明天实际天气状况和你预测的天气状况的KL散度为$D(P \|Q) =0.521$

然后我们可以发现：$0.884+0.521=1.405$

这里可以引出一个结论

从编码的角度解释

注意：下边这个举的例子是能整除的情况下，不能整除的情况下是算不出来的。

能整除的例子

假设我们现在有一条消息皮皮卡皮，皮卡丘。

让我们对这条消息统计一下：

字	皮	卡	丘	，
数量	4	2	1	1
比例	$\frac{4}{8}$	$\frac{2}{8}$	$\frac{1}{8}$	$\frac{1}{8}$

画个哈夫曼树：

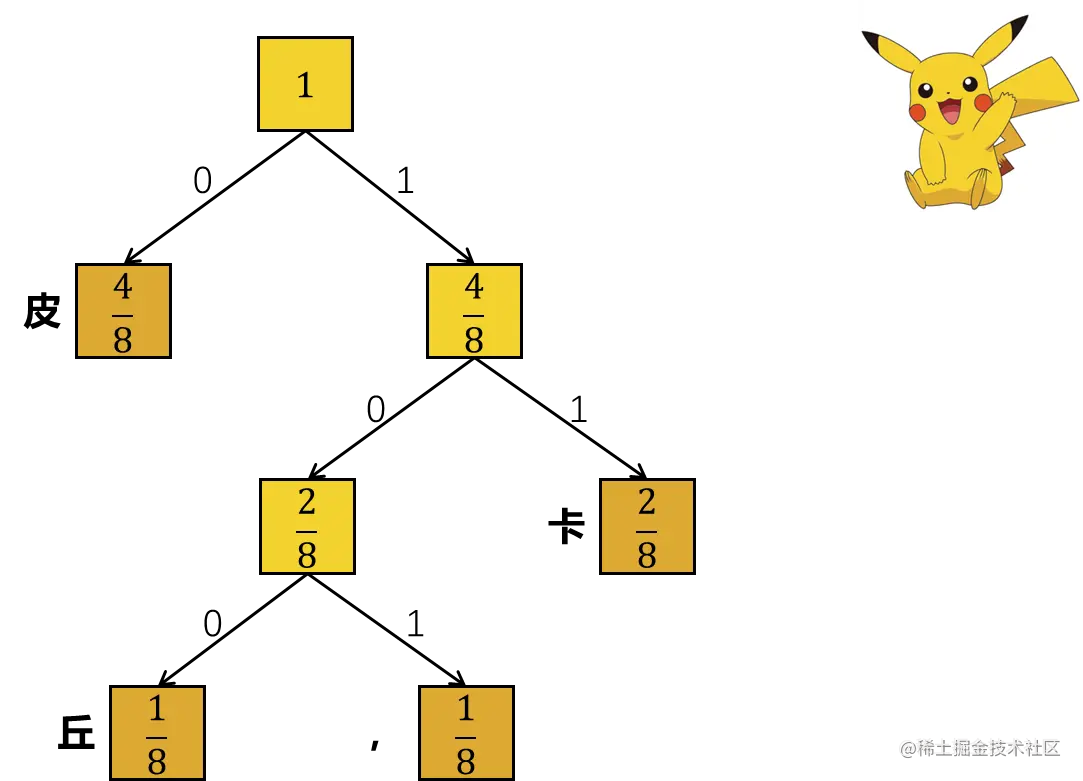
字	皮	卡	丘	，
数量	4	2	1	1
比例	$\frac{4}{8}$	$\frac{2}{8}$	$\frac{1}{8}$	$\frac{1}{8}$
哈夫曼编码	0	11	100	101
编码长度	1	2	3	3

最短编码平均长度：

$\frac{4}{8} \times 1+\frac{2}{8} \times 2+\frac{1}{8} \times 3+\frac{1}{8} \times 3=1.75$

上述编码的熵：

$-\frac{4}{8} \times \log \frac{4}{8}-\frac{2}{8} \times \log \frac{2}{8}-\frac{1}{8} \times \log \frac{1}{8}-\frac{1}{8} \times \log \frac{1}{8}=1.75$

从编码角度看，一串编码的熵等于它的最短编码平均长度。

字	皮	卡	丘	，
数量	4	2	1	1
比例	$\frac{4}{8}$	$\frac{2}{8}$	$\frac{1}{8}$	$\frac{1}{8}$
哈夫曼编码	0	11	100	101
错误的哈夫曼编码	11	0	100	101

如果你编码时候写错了

现在的平均编码长度是：

$\frac{4}{8} \times 2+\frac{2}{8} \times 1+\frac{1}{8} \times 3+\frac{1}{8} \times 3=2$

此时交叉熵为：

$-\frac{4}{8} \times \log \frac{2}{8}-\frac{2}{8} \times \log \frac{4}{8}-\frac{1}{8} \times \log \frac{1}{8}-\frac{1}{8} \times \log \frac{1}{8}=2$

使用错误的编码时候，编码平均长度就是交叉熵。

而KL散度呢？

$\frac{4}{8} \times \log(\frac{4}{8}\div\frac{2}{8})+\frac{2}{8} \times \log (\frac{2}{8} \div \frac{4}{8})+\frac{1}{8} \times \log (\frac{1}{8} \div \frac{1}{8})+\frac{1}{8} \times \log (\frac{1}{8} \div \frac{1}{8})=0.25$

KL散度就是错误编码平均长度和正确编码平均长度的差异。

不能整除的例子

注意：你看，不能整除的情况下是算不出来的。

假设我们现在有一条消息皮卡皮卡，皮卡皮，皮卡丘。

让我们对这条消息统计一下：

字	皮	卡	丘	，
数量	5	4	1	2
比例	$\frac{5}{12}$	$\frac{4}{12}$	$\frac{1}{12}$	$\frac{2}{12}$

画个哈夫曼树：

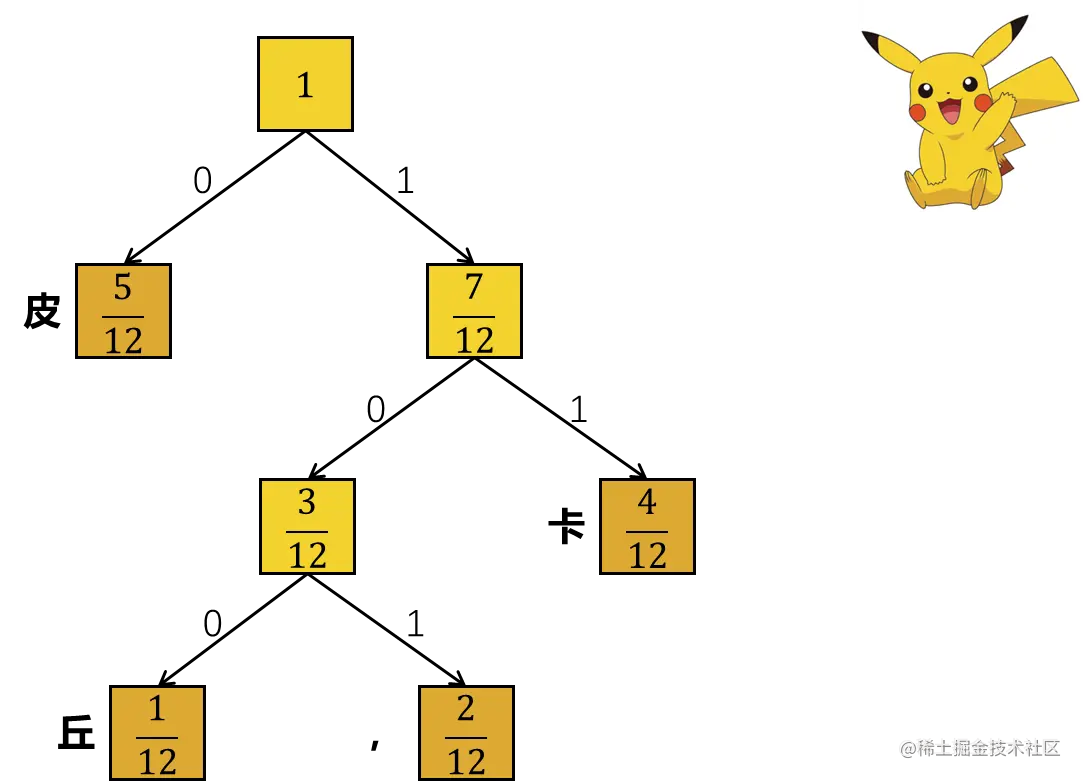
字	皮	卡	，	丘
数量	5	4	2	1
比例	$\frac{5}{12}$	$\frac{4}{12}$	$\frac{2}{12}$	$\frac{1}{12}$
哈夫曼编码	0	11	101	100
编码长度	1	2	3	3

最短编码平均长度：

$\frac{5}{12} \times 1 +\frac{4}{12} \times 2+\frac{2}{12} \times 3+\frac{1}{12} \times 3 = 1.83$

上述编码的熵：

$-\frac{5}{12} \times \log\frac{5}{12} -\frac{4}{12} \times \log\frac{4}{12}-\frac{2}{12} \times \log\frac{2}{12}-\frac{1}{12} \times \log\frac{1}{12} = 1.78$

后边不算了。可以看到不能整除情况下因为一些误差是不相等的。