word2vec过程详解

本文将对文章word2vec Parameter Learning Explained ——Xin Rong进行解读

摘要

word2vec是一种词嵌入模型，对单词进行one-hot编码得到的序列数据训练，得到 $d$ 维空间上的词向量，从而得到降维的效果。word2vec核心思想是根据多类分类任务构建模型，而词嵌入只是其中的一个副产物。word2vec包含两个模型，分别为CBOW(Continuous Bag-of-Word Model)和SG(skip-gram Model)。两种模型的思路一样，但损失函数稍微有点不一样。在看本文前，需要的前提知识：

了解一些经典的机器学习流程。
了解损失函数和梯度下降法的含义。
了解one-hot编码。
了解多分类任务，softmax交叉熵损失的意义。
了解稀疏概念。
了解条件概率。

一个机器学习模型的构建流程关键在于：

定义输入数据的类型。
定义计算过程。
定义损失函数。
定义参数更新方法。

1 Continuous Bag-of-Word Model

CBOW模型是基于上下文对中心词进行预测，首先基于one-hot编码对单词进行数据化，再投入到模型训练，得到的模型参数为降维后的词向量。

符号	说明
$V$	词典单词数
$N$	隐藏元个数(降维维度 $d$ )

1.1 One-word context

我们先讨论一个单词的任务。一个单词的任务主要思想是：降维后的词向量需要保持单词在词典中的位置信息。首先我们贴上一张过程图，随后对图的过程进行详解。

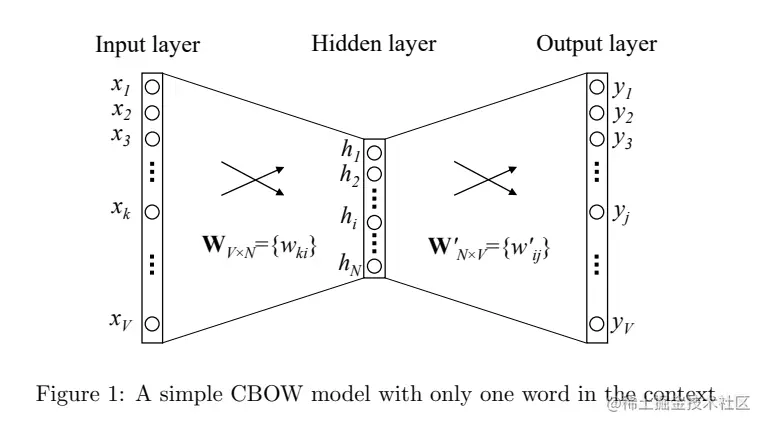
Step1、定义输入模型的数据(one-hot编码)

给定一个单词 $\mathbf{x}$ =“真香”，假设词典中单词数为 $V$ 个，假设 $\mathbf{x}$ 位于词典中第二个词，则根据one-hot编码可得， $\mathbf{x}=[0,1,0,0,\cdots,0]$ ，第二个位置编码为1，其他为0。目的是将 $X$ 进行降维。

Step2、前向计算，定义两个将向量进行"稠密化"的矩阵。

第一次计算：定义Input $\rightarrow$ Hidden的矩阵 $W$ ，定义 $W$ 矩阵维度为 $V\times N$ 。

\mathbf{h}=\mathbf{W}^{T} \mathbf{x}=\mathbf{W}_{(k,)}^{T}:=\mathbf{v}_{w_{I}}^{T}

其中 $\mathbf{v}_{w_{I}}^{T}$ 定义为降维后的单词向量，原文的意思是“is the vector representation of input word”，为了更直观的看出计算过程，将以"真香"为例，计算过程如下：

h=W^T\mathbf{x}=\left[ \begin{matrix} w_{11}& w_{12}& \cdots& w_{1N}\\ w_{21}& w_{22}& \cdots& w_{2N}\\ \vdots& \vdots& \ddots& \vdots\\ w_{V1}& w_{V2}& \cdots& w_{VN}\\ \end{matrix} \right] ^T\left[ \begin{array}{c} 0\\ 1\\ \vdots\\ 0\\ \end{array} \right] =\left[ \begin{matrix} w_{11}& w_{21}& \cdots& w_{V1}\\ w_{12}& w_{22}& \cdots& w_{V2}\\ \vdots& \vdots& \ddots& \vdots\\ w_{1N}& w_{2N}& \cdots& w_{VN}\\ \end{matrix} \right] \left[ \begin{array}{c} 0\\ 1\\ \vdots\\ 0\\ \end{array} \right] =\left[ \begin{array}{c} w_{21}\\ w_{22}\\ \vdots\\ w_{2N}\\ \end{array} \right]

即：

h^T=\mathbf{v}_{w_{I}}=\left[ \begin{matrix} w_{21}& w_{22}& \cdots& w_{2N}\\ \end{matrix} \right]

第二步计算：定义Hidden $\rightarrow$ Output的矩阵 $W'$ ，定义 $W'$ 矩阵维度为 $N\times V$ ，该矩阵的意义是将 $h$ 映射为和一开始输入one-hot变量一样长度为 $V$ 的向量进行输出，从而可以定义交叉熵损失函数。将以"真香"为例，计算过程为：

u=W'^Th=\left[ \begin{matrix} w_{11}'& w_{12}'& \cdots& w_{1V}'\\ w_{21}'& w_{22}'& \cdots& w_{2V}'\\ \vdots& \vdots& \ddots& \vdots\\ w_{N1}'& w_{N2}'& \cdots& w_{NV}'\\ \end{matrix} \right] ^T\left[ \begin{array}{c} w_{21}\\ w_{22}\\ \vdots\\ w_{2N}\\ \end{array} \right] =\left[ \begin{matrix} w_{11}'& w_{21}'& \cdots& w_{N1}'\\ w_{12}'& w_{22}'& \cdots& w_{N2}'\\ \vdots& \vdots& \ddots& \vdots\\ w_{1V}'& w_{2V}'& \cdots& w_{NV}'\\ \end{matrix} \right] \left[ \begin{array}{c} w_{21}\\ w_{22}\\ \vdots\\ w_{2N}\\ \end{array} \right] =\left[ \begin{array}{c} \sum\limits_{k=1}^N{w_{2k}w_{k1}'}\\ \sum\limits_{k=1}^N{w_{2k}w_{k2}'}\\ \vdots\\ \sum\limits_{k=1}^N{w_{2k}w_{kN}'}\\ \end{array} \right] _{V\times 1}=\left[ \begin{array}{c} u_1\\ u_2\\ \vdots\\ u_V\\ \end{array} \right]

化简上式，即为：

u_{j}=\mathbf{v}_{w_{j}}^{\prime T} \mathbf{h}

其中 $\mathbf{v}_{w_{j}}$ 是 $W'$ 的第 $j$ 列

第三步计算：定义Output的激活函数softmax。注意我们的任务是一个分类任务，而不是一个词嵌入任务，因此我们需要将第二步计算得到的 $u_j$ 进行softmax映射，得到总和为1的数值，定义得到的最终输出为：(此处需要了解softmax交叉熵损失函数具体参考简单的交叉熵损失函数，你真的懂了吗？ - 知乎 (zhihu.com))

p\left(w_{j} \mid w_{I}\right)=y_{j}=\frac{\exp \left(u_{j}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)} \tag{1}

(注意此处是一个单词的模型)还是以"真香"为例，我们输入 $\mathbf{x}$ =“真香”， $\mathbf{x}=[0,1,0,0,\cdots,0]$ 。

从图中可以看出，输出层有 $V$ 个 $y$ 值，根据多分类任务的思想，我们取最大的 $y_j$ ，输出结果则为成功分类到第 $j$ 类。
因此word2vec构建的模型可以看作是 $V$ 类分类任务( $V$ 是词典中的单词数)。
为了保持降维后的词向量是拥有在词典中的位置信息的，因此word2vec模型的目标是最大化 $y_2$ (因为"真香"位于第二个位置)。

那么有人就可能问了，输入一个词，构建一个模型分类识别出是这个词，那不是多此一举吗？

答：并不是多此一举，word2vec的目标产物并不是最终层的输出，而是模型的副产物，中间隐藏层 $W_{V\times N}$ 和 $W_{N\times V}'$ ，如输入”真香“，训练得到的对应模型参数W后，我们可以计算

W^T\mathbf{x}

从而查询“真香"对应的词向量为

h^T=\mathbf{v}_{w_{I}}=\left[ \begin{matrix} w_{21}& w_{22}& \cdots& w_{2N}\\\end{matrix} \right]

Step3、损失函数，从上述我们可以知道word2vec模型实际是一个分类任务，首先我们将公式(1)进行转化，带入 $u_j$ 的实际值，得到：

p\left(w_{j} \mid w_{I}\right)=\frac{\exp \left(\mathbf{v}_{w_{j}}^{\prime}{ }^{T} \mathbf{v}_{w_{I}}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(\mathbf{v}_{w_{j^{\prime}}}{ }^{T} \mathbf{v}_{w_{I}}\right)}

定义损失函数 $E$ 为：

\begin{aligned} \max p\left(w_{O} \mid w_{I}\right) &=\max y_{j^{*}} \\ &=\max \log y_{j^{*}} \\ &=u_{j^{*}}-\log \sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right):=-E, \end{aligned}

其中 $j^{*}$ 为输入词在词典的真实位置，如真香的位置是2，因此 $j^{*}=2$ ，从损失函数的定义可以看出，以真香为例，我们想要最大化 $y_2$ 。

Step4、方向传播参数更新：word2vec模型采用梯度下降法进行参数更新，由于本文是对word2vec的过程详解，主导过程的详解，因此将不详细进行推导，有兴趣的同学可以去看原文。

1.2 Multi-word context

本节我们将讨论多个单词的模型。在1.1节中，我们讨论了一个单词的模型，在一个单词模型中，word2vec只使用了单词在词典的位置信息。由于一个单词不可能是独立出现的，而是随着句子出现的，因此我们还可以利用单词在句子中的位置：即上下文。如将对句子"螺蛳粉真香啊"进行训练，首先对句子进行分词，分为"螺蛳粉"，”真香“，”啊"，我们假设"螺蛳粉"在词典的第1个位置，“啊”在第3个位置(这样假设是为了我写one-hot编码得到的向量)。同样，我们先贴一张过程图。

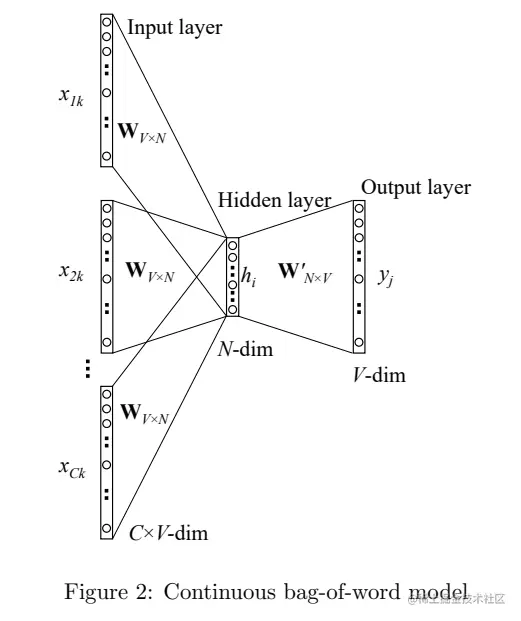
Step1、定义输入模型的数据(one-hot编码)

"螺蛳粉"： $\mathbf{x_1}=[1,0,0,0,\cdots,0]$
”真香“： $\mathbf{x_2}=[0,1,0,0,\cdots,0]$
”啊"： $\mathbf{x_3}=[0,0,1,0,\cdots,0]$

和一个单词模型(输入和输出目标一样)，不一样的是：模型目标为输入 $\mathbf{x_1}$ , $\mathbf{x_3}$ ，预测中心词 $\mathbf{x_2}$

Step2、和一个单词模型的Step1大致一样，不同的是在隐藏层中，我们将对得到的值进行平均化操作

\begin{aligned} \mathbf{h}&=\frac{1}{2}\mathbf{W}^T\left( \mathbf{x}_1+\mathbf{x}_3 \right)\\ &=\frac{1}{2}\left( \mathbf{v}_{w_1}+\mathbf{v}_{w_3} \right) ^T\\ \end{aligned}

Step3、由于是分类"真香"，因而和一个单词模型的损失函数一样，目标是让 $y_2$ 值最大化

\begin{aligned} E &=-\log p\left(w_{O} \mid w_{I, 1}, \cdots, w_{I, C}\right) \\ &=-u_{j^{*}}+\log \sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right) \\ &=-\mathbf{v}_{w_{O}}^{\prime}{ }^{T} \cdot \mathbf{h}+\log \sum_{j^{\prime}=1}^{V} \exp \left(\mathbf{v}_{w_{j}}^{\prime}{ }^{T} \cdot \mathbf{h}\right) \end{aligned}

Step4、同样为反向传播，梯度下降法。

2 Skip-Gram Model

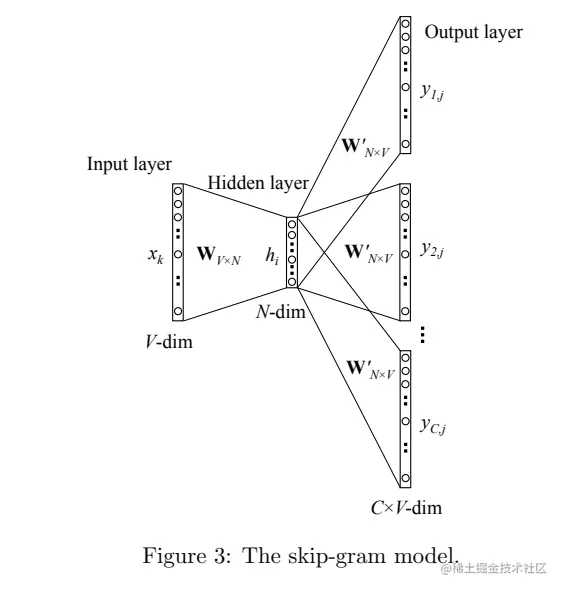
Skip-Gram Model 的思想是利用中心词预测上下文，具体操作是对损失函数进行修改。同样以句子"螺蛳粉真香啊"举例，首先对句子进行分词，分为"螺蛳粉"，”真香“，”啊"。我要预测出”真香“的上下文，即预测出”螺蛳粉“，”啊“。

因此模型修改为模型目标为输入中心词 $\mathbf{x_2}$ ，预测上下文 $\mathbf{x_1}$ , $\mathbf{x_3}$ ，根据one-hot编码信息，和下图对应的位置，我们需要对 $y_{11}$ 和 $y_{23}$ 最大化(因为 $y_{1,j}$ 对应的是 $\mathbf{x_1}$ ， $y_{2,j}$ 对应的是 $\mathbf{x_3}$ )。

其他过程类似，对应的损失函数修改为：

\begin{aligned} E &=-\log p\left(w_{O, 1}, w_{O, 2}, \cdots, w_{O, C} \mid w_{I}\right) \\ &=-\log \prod_{c=1}^{C} \frac{\exp \left(u_{c, j_{c}^{*}}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)} \\ &=-\sum_{c=1}^{C} u_{j_{c}^{*}}+C \cdot \log \sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right) \end{aligned}

存在的缺陷

word2vec模型的参数量很大，如 $2$ 万个词的词典，降维设定为 $256$ 维，则 $W$ 矩阵将有 $20000×256$
损失函数计算量过大，因为word2vec实际上是一个分类任务，如果是 $2$ 万个词的词典，将对应 $2$ 万类的分类模型，计算Softmax中的 $\sum_{j^{\prime}=1}^{V} \exp \left(\mathbf{v}_{w_{j^{\prime}}}{ }^{T} \mathbf{v}_{w_{I}}\right)$ 将变得十分困难。

目前word2vec采用的两种加速方法：Hierarchical Softmax，Negative Sampling。均是解决Softmax中的问题，有兴趣的同学自行了解。

Word2Vec过程详解(极易理解)