本项目代码已托管至github,将会随着博客实时更新进度
每一节的工程我都会创建一个新的分支,分支名由这一节的数字决定。
前言
上一节中我们已经实现了一个简单的光栅化,但是这其实是完全不足够的,一个合理的三角形光栅化过程值得开一整节去叙述。
但这一节讲的将不仅仅是光栅化的过程,严格意义上讲,三角形光栅化基本上就是寻找三角形并且对一些属性插值的过程。但实际上图形渲染管线还有很多杂七杂八的步骤,我也将在这一节中进行讨论。
一般来说,MVP变换到光栅化,中间还应当有一个裁剪的步骤。而光栅化后就是着色,也是我们fragment shader工作的地方。着色后需要一个深度测试检测遮挡,用来判断哪些面是应该渲染的,当然着色后可能会有很多种不同的测试,但是我们这里先只讨论深度测试。
所有的测试都完成后会进入屏幕后处理阶段,可以做一些滤镜的效果,也可以做知名的RayMarching算法来构建诸如大气散射体积云等效果,当然也可以什么都不做直接渲染出图像。
除此之外还需要一些简单的抗锯齿,而抗锯齿并不是一个固定的阶段,他可能发生在上述任何一个阶段,需要看具体算法而定。
其中,着色与屏幕后处理我们将在后续单独开新章节讲述,测试也许也会专门开章节吧。在这里我们将主要讲述的内容是裁剪、光栅化与深度测试。
封装Vertex类
因为我们马上就会需要用到大量的插值算法,而每个顶点上存储的所有属性都将会被插值。
我们目前只是用到了法线颜色和坐标,我们后面马上就会引入深度和纹理坐标等属性,为了不让我们重复花费时间在给每个属性插值上面,我们先抽象一个vertex类:
#pragma once
#include "myEigen.hpp"
#include "tgaimage.h"
namespace rst {
struct Vertex
{
myEigen::Vector4f vertex;
TGAColor vertexColor;
myEigen::Vector4f normal;
Vertex& operator=(const Vertex& v) {
vertex = v.vertex;
vertexColor = v.vertexColor;
normal = v.normal;
return *this;
}
};
inline Vertex lerp(const Vertex& v1, const Vertex& v2, const float t) {
return Vertex{
lerp(v1.vertex, v2.vertex, t),
ColorLerp(v1.vertexColor, v2.vertexColor, t),
lerp(v1.normal, v2.normal, t)
};
}
}
可以看到我们这里用到了一个颜色的插值函数,原本的tgaimage.h里并没有这个函数,这是我自己加的:
struct TGAColor {
std::uint8_t bgra[4] = { 0,0,0,0 };
std::uint8_t bytespp = { 0 };
TGAColor() = default;
TGAColor(const std::uint8_t R, const std::uint8_t G, const std::uint8_t B, const std::uint8_t A = 255) : bgra{ B,G,R,A }, bytespp(4) { }
TGAColor(const std::uint8_t* p, const std::uint8_t bpp) : bytespp(bpp) {
for (int i = bpp; i--; bgra[i] = p[i]);
}
std::uint8_t& operator[](const int i) { return bgra[i]; }
inline TGAColor operator+(const TGAColor& color) const {
return TGAColor(bgra[2] + color.bgra[2], bgra[1] + color.bgra[1], bgra[0] + color.bgra[0], bgra[3] + color.bgra[3]);
}
inline TGAColor operator*(const TGAColor& color) const {
return TGAColor(bgra[2] * color.bgra[2], bgra[1] * color.bgra[1], bgra[0] * color.bgra[0], bgra[3] * color.bgra[3]);
}
inline TGAColor operator*(const float t) const {
return TGAColor(bgra[2] * t, bgra[1] * t, bgra[0] * t, bgra[3] * t);
}
};
inline TGAColor ColorLerp(const TGAColor& color1, const TGAColor& color2, float t) {
return color1 * (1 - t) + color2 * t;
}
注意TGAColor类里存储的是bgra而非rgba,不要写反了。
基本上就这样就差不多了,记得修改下三角形类里的成员,都改成新的vertex类。
这样我们后续想给顶点添加属性只需要在这个类里修改就可以。
在光栅化之前
在上一节的MVP变换中,其实我们的处理是有一些问题的的,但是我们选择的测试用例并没有暴露出这些问题。
简单来说我们一直强调只有视椎体、正交视体或者是正交投影后的正则视体才可以被渲染,但是我们并没有实质上做剔除或者是裁剪操作,在最后的正则视体空间内,我们将坐标的xy映射到屏幕空间的对应坐标后,并没有对z值操作就直接就光栅化了坐标点。这样虽然正则视体x方向和y方向上的物体确确实实被排除了(被映射到了不属于屏幕空间范围内的坐标),但是近裁剪平面跟远裁剪平面以外的物体并没有被剔除或者裁剪,还是会被渲染到屏幕空间上。
所以我们现在最需要做的就是裁剪与剔除:
裁剪(Clip)与剔除(Cull)
注意:我们现在模拟的阶段对应的是GPU渲染管线上的裁剪,而非应用程序阶段的视椎体剔除。一般来说,物体在从cpu发送到gpu之前,我们会先在cpu内对每个物体造一个包围盒,再用包围盒跟视椎体进行计算,剔除那些包围盒都不跟视椎体有任何交叉的物体以减少draw call,而gpu端的剔除粒度更细,面对的对象是那些构成物体的图元。
注意区分裁剪与剔除这两个概念,剔除指的是将一个三角形,或者更准确地说一个图元完全删去。比如完全不在我们的视椎体内的三角形图元,或者物体背面的三角形图元需要被剔除。但是裁剪特指对于那些一部分在视体外,一部分在视体内的那种图元,我们需要对它们进行“裁剪”。
不过其实混用这两个概念应该也没事。。。大家应该都知道彼此在说什么。
裁剪与剔除其实是与MVP变换高度关联的步骤,也可以把这一小章节当做是对于上一节的补充。
虽然说裁剪与剔除看似只是为了加速我们的渲染流程,但实际上如果完全不做裁剪,我们渲染的图像肯定会出错误。大家回忆一下这玩意儿:
可以看出z在透视矩阵变换后变成了一个反比例函数,而x和y则乘以n再除以z,这意味着
1.z为0的时候计算会出错误。
2.n为0时会丢失所有坐标信息。
3.反比例函数则意味着位于摄像机后面的物体的z坐标反而被映射到了一个比摄像机前物体z坐标区间更小的区间,摄像机背后的物体也会被渲染出来。
对于2,我们只需要规定近裁剪平面不能与相机重合就行,最起码也得跟相机有那么一点距离,就像unity里的near clip plane最小值不能为0一样。
而对于1和3,我们只能通过裁剪那些近平面后的图元才能做到正确渲染想要的图像。
对于3发生的原因我们马上就会讨论到。
裁剪位于渲染管线的位置
现在最广泛运用的应该就是齐次坐标裁剪。
这个名词可能有些让人困惑,这就不得不提MVP变换中被我们一笔带过的那个过程了。
我们之前说过,透视投影矩阵会导致坐标的w变成了变换前的z值,想要继续走下一步需要先把坐标每项都除以w,也就是做“透视除法”。
但这里有大学问,做透视除法前的坐标可以看到是一个不折不扣的四维坐标,而它所在的空间被我们称作齐次裁剪空间,或者裁剪空间。我们所说的齐次坐标裁剪也就是在这个空间内进行。当裁剪完毕后,我们才会做透视除法,将空间转换为我们之前说的正则视体,或者简写称作CVV(canonical view volume),而CVV所在的坐标被我们称作NDC(normalized device coordinates),也就是归一化设备坐标。注意透视除法并没有把我们的空间变换到哪个新空间,只是变换到了归一化设备坐标系上。
那么是不是我们在裁剪空间就能一下裁剪完所有三角形呢?
应该也可以,但是判断一个三角形和一个box的裁剪非常复杂,比方说想象一个三角形三个顶点都在立方体外,却从中间穿过了立方体的情况,我们应该如何判断呢?
所以我在我的光栅器中简化问题,在齐次空间只做近远平面的裁剪,在屏幕空间再裁剪那些经过映射后跑出屏幕外的顶点。
所以我们先把渲染管线的顺序给分清:
void rasterizer::draw(std::vector<std::shared_ptr<rst::Triangle>>& TriangleList)
{
Transform projection = Perspective(zneardis, zfardis, fovY, aspect);
Transform mv = Camera(eye_pos, gaze_dir, view_up) * Modeling(myEigen::Vector3f(0),
myEigen::Vector3f(1),
myEigen::Vector3f(rotateAxis), theta);
Transform viewport = Viewport(width, height);
for (const auto& t : TriangleList)
{
Triangle NewTriangle = *t;
//Model Space -> World Space -> Camera Space
std::array<myEigen::Vector4f, 3> vert
{
(mv(t->vertex[0].vertex)),
(mv(t->vertex[1].vertex)),
(mv(t->vertex[2].vertex))
};
auto cameraSpacePos = vert;
//BackCulling
if (backCulling) {
}
//Transform Normal
auto normalMV = mv;
normalMV.toNormal();
std::array<myEigen::Vector4f, 3> normal
{
(normalMV(t->vertex[0].normal)),
(normalMV(t->vertex[1].normal)),
(normalMV(t->vertex[2].normal))
};
//Camera Space -> Homogeneous Clipping Space
for (auto& v : vert)
{
v = projection(v);
}
//Homogeneous Clipping
for (auto& v : vert)
{
}
//Homogeneous Clipping Space -> Canonical View Volume(CVV)
for (auto& v : vert)
{
v /= v.w;
}
//Canonical View Volume(CVV) -> Screen Space
for (auto& v : vert)
{
v = viewport(v);
}
for (size_t i = 0; i < 3; i++)
{
NewTriangle.setVertexPos(i, vert[i]);
NewTriangle.setColor(i, t->vertex[i].vertexColor);
NewTriangle.setNormal(i, normal[i]);
}
//Viewport Clipping
auto NewVert = clip_Cohen_Sutherland(NewTriangle, cameraSpacePos);
for (size_t i = 0; i < NewVert.size() - 2; i++)
{
rasterize_edge_walking(Triangle(NewVert[0], NewVert[1 + i], NewVert[2 + i]), cameraSpacePos);
}
}
}
为什么不在CVV内做裁剪?
经过上述的讲解,很容易想到的就是我们可以在NDC下对CVV进行裁剪,毕竟CVV是正则视体嘛,一个立方体想做些计算想想就很容易。
但是可惜的是不行。
做透视除法前,我们的z坐标变换前与变换后还是一个简单的线性关系:
但是做了透视除法后一切都不一样了,他们变成了一个反比例函数的关系:
这个过程使得我们之前说的问题3被暴露了出来,感兴趣的可以画画函数曲线,其中n和f都小于0。
画了函数曲线的话就可以看出,位于摄像机后面的物体的z坐标反而被映射到了一个比摄像机前物体z坐标区间更小的区间里,这给我们的裁剪算法反而带来了更多的麻烦,所以我们选择齐次坐标裁剪。
齐次坐标裁剪
我的软件光栅器中齐次坐标裁剪的方式仅供参考,并不代表实际的GPU是怎么处理裁剪系统的。实际的GPU应该只会严格裁剪近远平面的图元来确保光栅化结果正确,而对于屏幕空间即xy平面上,GPU会给一个比我们屏幕空间大得多的矩形来做裁剪判断,这样除非是越界得特别过分的图元,不然不会被裁剪。对于GPU来说,做一些复杂的裁剪算法,还不如让它用蛮力多算几个像素来的快。
齐次裁剪空间其实是一个四维空间,比较不太容易想象。但是我们可以通过这个式子来大致想象一下
因为我们所要得到的透视除法后的空间是CVV,是一个xyz区间皆在[-1, 1]内的正则立方体,我们可以反推得出x,y,z各自的取值范围:
其中w为物体透视变换前的z值。而变换前的z值显然需要在近远平面区间内,所以直接得出w的取值范围。(别忘了n和f都是负值)
既然是不等式,那么w的取值范围非常重要,w必须确定是负值还是正值,不然得出的式子肯定不一样,所以我们在这个阶段需要做的就是近远平面的裁剪,将w锁定在负值上。
//Homogeneous Clipping
for (auto& v : vert)
{
if (v.w > -zneardis || v.w < -zfardis) return;
}
Cohen-Sutherland算法
三角形的裁剪->线段的裁剪->顶点的裁剪
我们接着在屏幕空间处理那些超出屏幕的三角形,这里我们会用到编码裁剪算法
科恩-苏泽兰算法 - 维基百科,自由的百科全书 (wikipedia.org)
可以参考一下这个算法的内容,wiki里的介绍写的非常好,我建议直接看他的原文:
需要注意的是,这个裁剪需要对边,也就是线段进行裁剪,而我们三角形使用的是顶点来表示,我们定义一下线段类:
struct Line
{
Vertex v1;
Vertex v2;
bool isNull = false;
Line() :isNull(true){}
Line(const Vertex& v1, const Vertex& v2) :v1(v1), v2(v2) {}
};
我们照着一步一步来:
首先我们将三角形化成三个线段,并在clip_line函数里对每条线段的两个顶点进行编码
std::vector<myEigen::Vector4f> rasterizer::clip_Cohen_Sutherland(const Triangle& t)
{
auto v = t.vertex;
std::array<Line, 3> line
{
Line(v[0], v[1]),
Line(v[1], v[2]),
Line(v[2], v[0])
};
line[0] = clip_line(line[0]);
line[1] = clip_line(line[1]);
line[2] = clip_line(line[2]);
}
Line rasterizer::clip_line(const Line& line)
{
Vertex v[2];
v[0] = line.v1, v[1] = line.v2;
int code[2];
code[0] = 0, code[1] = 0;
const int left = 1;
const int right = 2;
const int bottom = 4;
const int top = 8;
for (size_t i = 0; i < 2; i++)
{
if (v[i].vertex.x < 0) code[i] = code[i] | 1;
if (v[i].vertex.x > width) code[i] = code[i] | 2;
if (v[i].vertex.y < 0) code[i] = code[i] | 4;
if (v[i].vertex.y > height) code[i] = code[i] | 8;
}
...
return Line(v[0], v[1]);
}
然后观察这个空间的编码结果来看看怎么对顶点进行裁剪:
很显然如果一条线段的两个顶点在同一侧,那么编码上总会有一个数字是相同的,即按位与运算结果不为0,这条线段将被丢弃。
否则将顶点与0001(左),0010(右), 0100(下), 1000(上)做按位与运算,结果不为零就说明在哪一个区域,我们将插值出新的顶点。
因为我们已经排除了两个顶点在同一侧的情况,所以如果顶点在左侧,那么另一个顶点一定在他右边,且我们可以直接求出插值权重weight=(左边界x - 左顶点x)/(右边界x-左边界x)来计算裁剪后的新顶点。
对于其他区域同理。
我们需要构建一个while大循环来给每一个顶点的两个坐标都进行类似的裁剪,while的退出条件即为两个顶点最终都被裁剪到0000这个区域内或者两个顶点在同一侧,所以循环中的clip_vert函数我们需要实时对编码进行更新:
Line rasterizer::clip_line(const Line& line,
const std::array<myEigen::Vector4f, 2>& clipSpacePos)
{
Vertex v[2];
v[0] = line.v1, v[1] = line.v2;
int code[2];
code[0] = 0, code[1] = 0;
const int left = 1;
const int right = 2;
const int bottom = 4;
const int top = 8;
auto vert1 = v[0];
auto vert2 = v[1];
for (size_t i = 0; i < 2; i++)
{
if (v[i].vertex.x < 0) code[i] = code[i] | 1;
if (v[i].vertex.x > width) code[i] = code[i] | 2;
if (v[i].vertex.y < 0) code[i] = code[i] | 4;
if (v[i].vertex.y > height) code[i] = code[i] | 8;
}
while (code[0] != 0 || code[1] != 0)
{
if ((code[0] & code[1]) != 0) return Line();
vert1 = clip_vert(vert1, vert2, code[0], code[1], 0, width, 0, height, { clipSpacePos[0], clipSpacePos[1] });
vert2 = clip_vert(vert2, vert1, code[1], code[0], 0, width, 0, height, { clipSpacePos[1], clipSpacePos[0] });
}
return Line(vert1, vert2);
}
然后我们来着手实现这个clip_vert函数对顶点进行裁剪并且实时更新编码值。
需要注意的是,我们的顶点经过裁剪后都是落到边界直线上,但是我们更新编码值的方法并没有界定落到边上的顶点如何给定编码,那么我们该怎么做呢?
解决方案很简单,我们以这条线段为例。
这条线段两个顶点不在同一侧,所以不会被提前删掉,进入第一次顶点裁剪。
先对(x1,y1)进行左裁剪,裁剪后落到左边界这条直线上,我们可以给x坐标加0.001,他就进入了1000区域,而不是落在便捷上了。
那么在下一次循环中这两个顶点就会落到同一侧,while循环就会结束,并返回一条空线段。
static Vertex clip_vert(const Vertex& _v1, const Vertex& _v2, int& code1, const int& code2,
const int leftBound, const int rightBound, const int bottomBound, const int topBound,
const std::array<myEigen::Vector4f, 2>& clipSpacePos)
{
const int left = 1;
const int right = 2;
const int bottom = 4;
const int top = 8;
auto v1 = _v1;
auto& v2 = _v2;
if ((left & code1) != 0)
{
float lerpNumber = (leftBound - v1.vertex.x) / (v2.vertex.x - v1.vertex.x);
v1 = perspectiveLerp(_v1, _v2, lerpNumber, clipSpacePos[0], clipSpacePos[1]);
v1.vertex = lerp(_v1.vertex, _v2.vertex, lerpNumber);
v1.vertex.x += 0.001f;
}
else if ((right & code1) != 0)
{
float lerpNumber = (v1.vertex.x - rightBound) / (v1.vertex.x - v2.vertex.x);
v1 = perspectiveLerp(_v1, _v2, lerpNumber, clipSpacePos[0], clipSpacePos[1]);
v1.vertex = lerp(_v1.vertex, _v2.vertex, lerpNumber);
v1.vertex.x -= 0.001f;
}
else if ((bottom & code1) != 0)
{
float lerpNumber = (bottomBound - v1.vertex.y) / (v2.vertex.y - v1.vertex.y);
v1 = perspectiveLerp(_v1, _v2, lerpNumber, clipSpacePos[0], clipSpacePos[1]);
v1.vertex = lerp(_v1.vertex, _v2.vertex, lerpNumber);
v1.vertex.y += 0.001f;
}
else if ((top & code1) != 0)
{
float lerpNumber = (v1.vertex.y - topBound) / (v1.vertex.y - v2.vertex.y);
v1 = perspectiveLerp(_v1, _v2, lerpNumber, clipSpacePos[0], clipSpacePos[1]);
v1.vertex = lerp(_v1.vertex, _v2.vertex, lerpNumber);
v1.vertex.y -= 0.001f;
}
code1 = 0;
if (v1.vertex.x < leftBound) code1 = (code1 | left);
if (v1.vertex.x > rightBound) code1 = (code1 | right);
if (v1.vertex.y < bottomBound) code1 = (code1 | bottom);
if (v1.vertex.y > topBound) code1 = (code1 | top);
return v1;
}
注意一下我们用到的这个插值函数不是我们之前定义的lerp函数,这是因为如果在屏幕空间上对三维或者四维空间中的三角形进行插值的时候需要做透视矫正。
若想详细了解,请往下翻到透视矫正这一小节。
我们的顶点和线段裁剪完后,发送给主函数的是顶点的数组,我们现在需要把他们装成一个个的三角形:
std::vector<Vertex> rasterizer::clip_Cohen_Sutherland(const Triangle& t,
const std::array<myEigen::Vector4f, 3>& clipSpacePos)
{
auto v = t.vertex;
std::array<Line, 3> line
{
Line(v[0], v[1]),
Line(v[1], v[2]),
Line(v[2], v[0])
};
line[0] = clip_line(line[0], { clipSpacePos[0], clipSpacePos[1] });
line[1] = clip_line(line[1], { clipSpacePos[1], clipSpacePos[2] });
line[2] = clip_line(line[2], { clipSpacePos[2], clipSpacePos[0] });
for (size_t i = 0; i < 2; i++)
{
if (line[i].isNull)
{
if (i == 0) {
line[i].v1 = line[2].v2;
line[i].v2 = line[1].v1;
}
else if (i == 1)
{
line[i].v1 = line[0].v2;
line[i].v2 = line[2].v1;
}
else if (i == 2)
{
line[i].v1 = line[1].v2;
line[i].v2 = line[0].v1;
}
}
}
std::vector<Vertex> newVert;
newVert.reserve(3);
if (fabs(line[2].v2.vertex.x - line[0].v1.vertex.x) < 0.0001f && fabs(line[2].v2.vertex.y - line[0].v1.vertex.y) < 0.0001f)
{
newVert.emplace_back(line[0].v1);
}
else
{
newVert.emplace_back(line[2].v2);
newVert.emplace_back(line[0].v1);
}
if (fabs(line[0].v2.vertex.x - line[1].v1.vertex.x) < 0.0001f && fabs(line[0].v2.vertex.y - line[1].v1.vertex.y) < 0.0001f)
{
newVert.emplace_back(line[1].v1);
}
else
{
newVert.emplace_back(line[0].v2);
newVert.emplace_back(line[1].v1);
}
if (fabs(line[1].v2.vertex.x - line[2].v1.vertex.x) < 0.0001f && fabs(line[1].v2.vertex.y - line[2].v1.vertex.y) < 0.0001f)
{
newVert.emplace_back(line[2].v1);
}
else
{
newVert.emplace_back(line[1].v2);
newVert.emplace_back(line[2].v1);
}
return newVert;
}
让我们看看结果:
大功告成!看起来是没有什么问题。不过旋转方向跟上一节的相反了,这不是我代码哪里写错了,是因为我现在才发现上一节做gif的时候图片顺序搞反了。。。导致上一节的旋转方向是反的,因为是“倒放”。
背面剔除
很多时候,如果一个三角形背对着我们的时候,我们可以直接把他们剔除掉,因为大部分时候,我们处理的模型都是闭合模型,所以只需要渲染三角形朝向外面的面,对于三角形朝向内部的面我们直接剔除,可以大大减小算力。
这个做起来很简单,如果三角形顶点绕序是逆时针的话,我们用顶点依次相减得出两个三角形内部向量,再叉乘得到的法向量应该是指向摄像机的,我们再将三角形任意一个点跟摄像机位置连成一个向量,这两个向量点积得出的结果应该是负数,若不是负数则意味着是背面,需要剔除。
顶点绕序是顺时针的话反过来就行了。
相机空间的相机坐标是(0, 0, 0),显然最适合做背面剔除,而且三角形光栅化可能会改变顶点顺序,所以相机空间做背面剔除无疑是非常合适的:
void rasterizer::TurnOnBackCulling()
{
this->backCulling = true;
}
void rasterizer::TurnOffBackCulling()
{
this->backCulling = false;
}
...
//BackCulling
if (backCulling) {
auto v1 = vert[1] - vert[0];
auto v2 = vert[2] - vert[1];
auto v = myEigen::crossProduct(myEigen::Vector3f(v1.x, v1.y, v1.z), myEigen::Vector3f(v2.x, v2.y, v2.z));
auto gaze = myEigen::Vector3f(vert[0].x, vert[0].y, vert[0].z);
if (vertexOrder == TriangleVertexOrder::counterclockwise)
{
if (myEigen::dotProduct(v, gaze) >= 0) return;
}
else
{
if (myEigen::dotProduct(v, gaze) <= 0) return;
}
}
但是背面剔除是一个需要选择开启的功能,因为他对模型提出了闭合的要求,如果对于像草、树叶这些不闭合的模型来说,我们不能开启背面剔除,否则草只能看到一个面,我们绕到背面去看草就消失了,这肯定是不对的。而且为了演示方便,这一节里我也不会开启背面剔除。
三角形光栅化
接下来我们要做的就是给三角形内部进行填色,我们将不只是满足于之前的线框渲染模式,我们将渲染出实心三角形。
三角形光栅化,说白了就是两个步骤,第一步是如何找到需要被光栅化的点,第二部是给需要被光栅化的点插值出需要的颜色、法线等属性。
Edge Walking
Edge Walking是一种常用于CPU软光栅的一种算法,有的人会把他称作扫描线算法,因为确实很像一根扫描线在上下来回扫描。
因为线段可以当做点的集合。那么我们不再计算孤立的一个点是否在三角形内,而是用水平的线来代替点。然后找到这条线与三角形的两个交点,自然两个交点中间的所有点都是我们这条线上的在三角形内部的点了。然后我们将线段往上移动一个像素再重复上述操作,直到三角形被“扫描”完全为止,这里的线段我们称之为“扫描线”。
我们先把三角形以y坐标第二大的顶点为界分为两个部分,上三角形和下三角形。
void rasterizer::rasterize_edge_walking(const Triangle& m)
{
Triangle t = m;
if (t.vertex[0].vertex.y > t.vertex[1].vertex.y)
std::swap(t.vertex[0], t.vertex[1]);
if (t.vertex[0].vertex.y > t.vertex[2].vertex.y)
std::swap(t.vertex[0], t.vertex[2]);
if (t.vertex[1].vertex.y > t.vertex[2].vertex.y)
std::swap(t.vertex[1], t.vertex[2]);
}
这样我们给三角形的顶点按从下到上排了个序,分界线就在vertex[2].vertex.y这根线上。
然后再对每个分割出来的三角形从下到上做扫描线,求出扫描线同三角形边相交的点。
这里求交点其实不需要靠什么直线方程来解决,可以直接通过线性插值来得到交点的坐标以及颜色等等。线性插值的系数t可通过当前扫描线的y坐标得到。
然后用这两个点给线段中的每一个像素再进行一次线性插值。这里给出下半部分三角形的代码:
float longEdge = t.vertex[2].vertex.y - t.vertex[0].vertex.y;
if (longEdge == 0) { return; }
//scan the bottom triangle
for (int y = std::ceil(t.vertex[0].vertex.y - 0.5f); y < std::ceil(t.vertex[1].vertex.y - 0.5f); y++)
{
float shortEdge = t.vertex[1].vertex.y - t.vertex[0].vertex.y;
float shortLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / shortEdge;
float longLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / longEdge;
Vertex shortVertex = lerp(t.vertex[0], t.vertex[1], shortLerp);
Vertex longVertex = lerp(t.vertex[0], t.vertex[2], longLerp);
if (shortVertex.vertex.x > longVertex.vertex.x)
std::swap(shortVertex, longVertex);
for (int i = std::ceil(shortVertex.vertex.x - 0.5f); i < std::ceil(longVertex.vertex.x - 0.5f); i++)
{
float lerpNumber = ((float)i + 0.5f - shortVertex.vertex.x) / (longVertex.vertex.x - shortVertex.vertex.x);
Vertex pixel = lerp(shortVertex, longVertex, lerpNumber);
image.set(i, y, pixel.vertexColor);
}
}
一定要注意精度问题!切记我们用屏幕中心的点的坐标来当做实际位置进行线性插值,但是image.set()里传入的两个int类型的坐标为像素左下角的坐标,一定要分清楚这个, 不然要么渲染相邻三角形的时候可能会出现缝隙,要么我们以后做抗锯齿的时候会很痛苦。
我们一般认为一个像素的中心在三角形内,那么这个像素就在三角形内。但如果三角形的边缘刚好穿过像素中心呢?从我们的代码可以看出来,一条扫描线穿过时,如果起点正好在像素中心,那么我们认为这个像素也在三角形内,但是终点如果在像素中心,那么我们认为这个像素不在三角形内。而如果是切割三角形的那条线穿过像素中心的话,我们认为这个像素属于下面那个三角形。看起来挺随意,但是可不能乱来,这都是有讲究的,我们在介绍另一种光栅化算法的时候将会着重提到具体的规则。
再加上渲染上半部分三角形的代码:
//scan the top triangle
for (int y = std::ceil(t.vertex[1].vertex.y - 0.5f); y < std::ceil(t.vertex[2].vertex.y - 0.5f); y++)
{
float shortEdge = t.vertex[2].vertex.y - t.vertex[1].vertex.y;
float shortLerp = ((float)y + 0.5f - t.vertex[1].vertex.y) / shortEdge;
float longLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / longEdge;
Vertex shortVertex = lerp(t.vertex[1], t.vertex[2], shortLerp);
Vertex longVertex = lerp(t.vertex[0], t.vertex[2], longLerp);
if (shortVertex.vertex.x > longVertex.vertex.x)
std::swap(shortVertex, longVertex);
for (int i = std::ceil(shortVertex.vertex.x - 0.5f); i < std::ceil(longVertex.vertex.x - 0.5f); i++)
{
float lerpNumber = ((float)i + 0.5f - shortVertex.vertex.x) / (longVertex.vertex.x - shortVertex.vertex.x);
Vertex pixel = lerp(shortVertex, longVertex, lerpNumber);
image.set(i, y, pixel.vertexColor);
}
}
当然为了代码简洁我们肯定需要试着将这两个for循环合并到一起,不过这样又不是不能跑,我懒得写在一起,就先这样了,看看渲染结果:
看着挺对的,可实际上对吗?
我们的插值其实并不对,还记得我们说过透视变换不是线性变换吗?那么屏幕空间的线性插值怎么能跟正常三维空间透视变换前的三角形的线性插值相提并论呢?
2D空间下的透视矫正插值
这里引用一张虎书的插图,来直观地理解为什么屏幕空间的线性插值不正确:
这两张图都是4x4的正方形平面,被分割成了平均的16块。
左边那张图显然符合我们的生活常识,即使这些方格实际上都是一样大的,但是因为近大远小的关系看起来应该是左边这样扭曲过的,而右边的是直接用屏幕空间的线性插值顶点位置出来的结果。这显然不对,因为他把正方形经过透视投影变换而成的梯形当作原始图形来线性插值了,而我们想要的结果是透视投影前先做线性插值,再做透视投影变换。
这显然是做不到的,因为我们线性插值前需要先找到屏幕空间应该被光栅化的像素,怎么可能先线性插值再变换到屏幕空间呢?
所以我们需要从屏幕空间的像素坐标反推出它在透视投影变换前位于相机空间的哪个点,找出一个映射关系。
大家可以借鉴一下这篇文章的推导过程:
我这里直接给出他的结果
m是屏幕空间下我们想要光栅化的像素的插值权重,n是这个像素对应到相机空间中的点的实际插值权重,Z1和Z2分别是我们要插值的两个坐标在相机空间下的深度值。
其中我们知道相机空间下的深度值在透视投影后变成了齐次裁剪空间中坐标的w值,所以我们可以只传递裁剪空间下的w值来计算。
inline Vertex perspectiveLerp(const Vertex& v1, const Vertex& v2, const float t,
const myEigen::Vector4f& v1c, const myEigen::Vector4f& v2c)
{
float correctLerp = t * v2c.w / ((1 - t) * v1c.w + t * v2c.w);
return lerp(v1, v2, correctLerp);
}
完整的透视校正下的EdgeWalking的代码如下:
void rasterizer::rasterize_edge_walking(const Triangle& m, const std::array<myEigen::Vector4f, 3>& clipSpacePos)
{
Triangle t = m;
auto csp = clipSpacePos;
if (t.vertex[0].vertex.y > t.vertex[1].vertex.y)
std::swap(t.vertex[0], t.vertex[1]); std::swap(csp[0], csp[1]);
if (t.vertex[0].vertex.y > t.vertex[2].vertex.y)
std::swap(t.vertex[0], t.vertex[2]); std::swap(csp[0], csp[2]);
if (t.vertex[1].vertex.y > t.vertex[2].vertex.y)
std::swap(t.vertex[1], t.vertex[2]); std::swap(csp[1], csp[2]);
float longEdge = t.vertex[2].vertex.y - t.vertex[0].vertex.y;
if (longEdge == 0) { return; }
//scan the bottom triangle
for (int y = std::ceil(t.vertex[0].vertex.y - 0.5f); y < std::ceil(t.vertex[1].vertex.y - 0.5f); y++)
{
float shortEdge = t.vertex[1].vertex.y - t.vertex[0].vertex.y;
float shortLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / shortEdge;
float longLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / longEdge;
Vertex shortVertex = lerp(t.vertex[0], t.vertex[1], shortLerp);
Vertex longVertex = lerp(t.vertex[0], t.vertex[2], longLerp);
Vertex shortVertexC = perspectiveLerp(t.vertex[0], t.vertex[1], shortLerp, csp[0], csp[1]);
Vertex longVertexC = perspectiveLerp(t.vertex[0], t.vertex[2],longLerp, csp[0], csp[2]);
if (shortVertex.vertex.x > longVertex.vertex.x)
std::swap(shortVertex, longVertex);
for (int i = std::ceil(shortVertex.vertex.x - 0.5f); i < std::ceil(longVertex.vertex.x - 0.5f); i++)
{
float lerpNumber = ((float)i + 0.5f - shortVertex.vertex.x) / (longVertex.vertex.x - shortVertex.vertex.x);
Vertex pixel = perspectiveLerp(shortVertex, longVertex, lerpNumber, shortVertexC.vertex, longVertexC.vertex);
image.set(i, y, pixel.vertexColor);
}
}
//scan the top triangle
for (int y = std::ceil(t.vertex[1].vertex.y - 0.5f); y < std::ceil(t.vertex[2].vertex.y - 0.5f); y++)
{
float shortEdge = t.vertex[2].vertex.y - t.vertex[1].vertex.y;
float shortLerp = ((float)y + 0.5f - t.vertex[1].vertex.y) / shortEdge;
float longLerp = ((float)y + 0.5f - t.vertex[0].vertex.y) / longEdge;
Vertex shortVertex = lerp(t.vertex[1], t.vertex[2], shortLerp);
Vertex longVertex = lerp(t.vertex[0], t.vertex[2], longLerp);
Vertex shortVertexC = perspectiveLerp(t.vertex[1], t.vertex[2], shortLerp, csp[1], csp[2]);
Vertex longVertexC = perspectiveLerp(t.vertex[0], t.vertex[2], longLerp, csp[0], csp[2]);
if (shortVertex.vertex.x > longVertex.vertex.x)
std::swap(shortVertex, longVertex);
for (int i = std::ceil(shortVertex.vertex.x - 0.5f); i < std::ceil(longVertex.vertex.x - 0.5f); i++)
{
float lerpNumber = ((float)i + 0.5f - shortVertex.vertex.x) / (longVertex.vertex.x - shortVertex.vertex.x);
Vertex pixel = perspectiveLerp(shortVertex, longVertex, lerpNumber, shortVertexC.vertex, longVertexC.vertex);
image.set(i, y, pixel.vertexColor);
}
}
}
我们输出一下结果:
怎么感觉废了半天劲没啥变化?
让我们在GeoGebra计算器套件里看一下这个式子的函数图像
Z1与Z2的差值越大,这个函数就越“凸”,也就是矫正与否的差别越大,而我们的三角形一是因为初始z值都是-2,在旋转中也拉不开太大距离。二是因为透视矫正在矫正顶点颜色插值的时候也不是很明显。所以我们的图像看起来与之前相差无几。可以使用photoshop叠图试试,或者加一行
if (fabs(correctLN - 0.5) < 0.05)pixel.vertexColor = TGAColor(255, 255, 255, 0);
把三角形的分割线中点与顶点的线段给画出来,再打开ps叠图,可以看到确实矫正后的中点判断比屏幕空间直接插值的结果有一个偏移量。
我的debug模式下渲染71帧时间差不多5.8秒左右,看起来这个算法确实不错,我们现在已经可以像这个表情包里一样说"I know opengl"了。
Edge Equation
我们这里还要介绍一种更广泛运用在GPU硬件上的算法。也就是Edge Equation。GAMES101作业框架中用的也是这种方法。
Edge Walking虽然也很好用,但他其实在GPU时代已经被淘汰了,虽然我们的软光栅确实还有Edge Walking的一席之地,但不要忘了我们做软光栅不是为了做软光栅,而是为了更深刻地理解一些渲染基础知识。那么我们一定需要了解Edge Equation,或者说,一定需要了解三角形的重心坐标插值。
Edge Equation判断点是否在三角形内的方法比较简单粗暴,直接计算出三角形三条边的方程,即Ax+By+C=0,然后把点的坐标直接代进去,因为直线会把屏幕分割成两个部分, 我们将代入出来的结果跟0比较,就可以知道点在哪个部分了。
然后我们把点的坐标代入三条直线方程,得出来的结果都大于0或者都小于0即代表点是否在三角形的内部。
GAMES101中闫令琪老师给了一个向量叉乘的算法,其实跟Edge Equation是等价的,算是换了一种方式理解直线方程。
当然我们需要做一个包围盒把三角形包起来,再遍历包围盒里的点,不然一个可能只占十几个像素的三角形我们都要遍历屏幕的每个像素的话就太扯淡了:
void rasterizer::rasterize_edge_equation(const Triangle& m, const std::array<myEigen::Vector4f, 3>& clipSpacePos)
{
int boundingTop = std::ceil(std::max({ m.vertex[0].vertex.y, m.vertex[1].vertex.y, m.vertex[2].vertex.y }));
int boundingBottom = std::floor(std::min({ m.vertex[0].vertex.y, m.vertex[1].vertex.y, m.vertex[2].vertex.y }));
int boundingRight = std::ceil(std::max({ m.vertex[0].vertex.x, m.vertex[1].vertex.x, m.vertex[2].vertex.x }));
int boundingLeft = std::floor(std::min({ m.vertex[0].vertex.x, m.vertex[1].vertex.x, m.vertex[2].vertex.x }));
for (int y = boundingBottom; y < boundingTop; y++)
{
for (int x = boundingLeft; x < boundingRight; x++)
{
if (insideTriangle(m, (float)x + 0.5, (float)y + 0.5))
{
}
}
}
}
static bool insideTriangle(const Triangle& m, const float x, const float y)
{
myEigen::Vector4f v1 = m.vertex[0].vertex;
myEigen::Vector4f v2 = m.vertex[1].vertex;
myEigen::Vector4f v3 = m.vertex[2].vertex;
float side1 = (v2.y - v1.y) * x + (v1.x - v2.x) * y + v2.x * v1.y - v1.x * v2.y;
float side2 = (v3.y - v2.y) * x + (v2.x - v3.x) * y + v3.x * v2.y - v2.x * v3.y;
float side3 = (v1.y - v3.y) * x + (v3.x - v1.x) * y + v1.x * v3.y - v3.x * v1.y;
return (side1 >= 0 && side2 >= 0 && side3 >= 0) || (side1 <= 0 && side2 <= 0 && side3 <= 0);
}
这时我们就需要注意到三角形的边缘绘制问题了,如果一个三角形的边缘刚好经过了像素的中心,那这个像素算在三角形里吗?
闫令琪老师说不用特殊处理,对,但是也不对。
我们现在接触的目前还只是不透明物的渲染,如果涉及到半透明物体的渲染的时候。如果一对相邻三角形的临边穿过了像素中心点,我们如果对两个三角形都认为这个像素算在三角形里的话,会导致两个三角形在这个顶点的颜色叠加在一起,也就是overdraw了,图像渲染得不正确。
而如果我们认为这样的像素不在三角形里的话,很明显连不透明物体的渲染都会出问题,两条三角形的临边会看起来挖了洞一样。
所以不能摆烂不作处理,我们需要规定一个规则来规范边缘像素的所有权。
Top-Left Rules
这个规则是directx3D的处理规则,我们可以参考他们的规则来做。
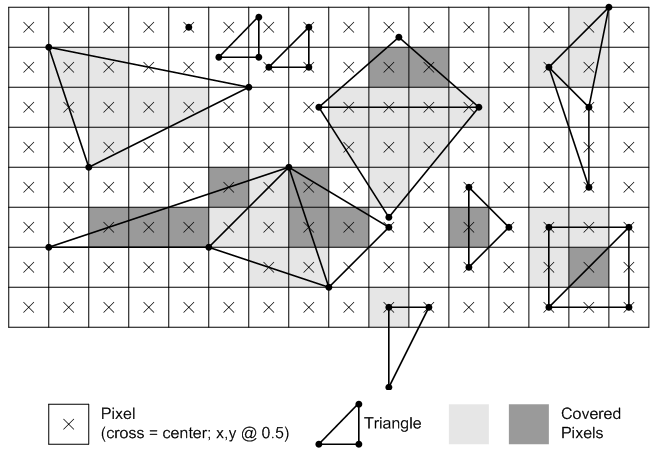
对于一条边跨过像素中心的情况,我们规定,如果这条边不是水平的,那么如果这条边是三角形“左边”的边,那么就属于三角形内。
如果这条边水平,那么如果这条边是三角形“上边”的边,那么就属于三角形内。
如何判断这条边是在topleft还是在bottomright呢?根据三角形的绕序来决定。
如果三角形绕序是逆时针的,那么可想而知,假设这条边的两个顶点分别为v1和v2,如果v1的y值大于v2的y值就说明这条边是三角形的“左”边,如果y值相同,那么v1的x值大于v2的x值就说明这条边是三角形的“上”边。
在实际代码中,我们的rules函数可以直接返回一个bias来影响判断:
static int TopLeftRules(const float side, const myEigen::Vector4f& v1, const myEigen::Vector4f& v2,
const rst::TriangleVertexOrder& Order)
{
if (Order == TriangleVertexOrder::counterclockwise) {
if (fabs(side) < 1e-6) {
return ((v1.y > v2.y) || (v1.y == v2.y && v1.x > v2.x)) ? 0 : -1;
} else { return 0; }
}
else
{
if (fabs(side) < 1e-6) {
return ((v1.y < v2.y) || (v1.y == v2.y && v1.x < v2.x)) ? 0 : -1;
}
else { return 0; }
}
}
bool rasterizer::insideTriangle(const Triangle& m, const float x, const float y)
{
myEigen::Vector4f v1 = m.vertex[0].vertex;
myEigen::Vector4f v2 = m.vertex[1].vertex;
myEigen::Vector4f v3 = m.vertex[2].vertex;
float side1 = (v2.y - v1.y) * x + (v1.x - v2.x) * y + v2.x * v1.y - v1.x * v2.y;
float side2 = (v3.y - v2.y) * x + (v2.x - v3.x) * y + v3.x * v2.y - v2.x * v3.y;
float side3 = (v1.y - v3.y) * x + (v3.x - v1.x) * y + v1.x * v3.y - v3.x * v1.y;
side1 += TopLeftRules(side1, v1, v2, vertexOrder);
side2 += TopLeftRules(side2, v2, v3, vertexOrder);
side3 += TopLeftRules(side3, v3, v1, vertexOrder);
return (side1 >= 0 && side2 >= 0 && side3 >= 0) || (side1 <= 0 && side2 <= 0 && side3 <= 0);
}
三角形重心坐标系插值
判断完毕了那些像素点需要被光栅化后,我们下一步就是插值出每个像素点的属性值,不同于edge walking两次线性插值的是,edge equation中使用三角形重心坐标来插值。
数学上定义了三角形重心坐标系,我们来回顾一下相关知识。
这里借用虎书的插图
想象这么一个坐标系,基向量为c-a和b-a,原点为a,那么点p可以这么表示:
我们把括号里的项拆出来
令α=1-β-γ,
那么我们定义一个三角形内的任何一个点p都可以用一个关于顶点A、B、C的线性组合来表示
其中α、β和γ都在(0, 1)范围内时才满足在三角形内的条件。
至于β和γ满足以下线性变换方程:
如果我们定义了二维矩阵就可以傻瓜式写出代码了,但是我们数学库里没定义这玩意儿。。。
所以直接求出结果代入吧:
我们直接转换成代码:
"rasterizer.cpp"
void rasterizer::rasterize_edge_equation(const Triangle& m, const std::array<myEigen::Vector4f, 3>& clipSpacePos)
{
int boundingTop = std::ceil(std::max({ m.vertex[0].vertex.y, m.vertex[1].vertex.y, m.vertex[2].vertex.y }));
int boundingBottom = std::floor(std::min({ m.vertex[0].vertex.y, m.vertex[1].vertex.y, m.vertex[2].vertex.y }));
int boundingRight = std::ceil(std::max({ m.vertex[0].vertex.x, m.vertex[1].vertex.x, m.vertex[2].vertex.x }));
int boundingLeft = std::floor(std::min({ m.vertex[0].vertex.x, m.vertex[1].vertex.x, m.vertex[2].vertex.x }));
for (int y = boundingBottom; y < boundingTop; y++)
{
for (int x = boundingLeft; x < boundingRight; x++)
{
if (insideTriangle(m, (float)x + 0.5, (float)y + 0.5))
{
Vertex pixel = barycentricLerp(m, myEigen::Vector2f(x + 0.5, y + 0.5));
image.set(x, y, pixel.vertexColor);
}
}
}
}
"geometry.cpp":
Vertex barycentricLerp(const Triangle& t, const myEigen::Vector2f& pixel)
{
Vertex v1 = t.vertex[0]; Vertex v2 = t.vertex[1]; Vertex v3 = t.vertex[2];
float xa = v1.vertex.x; float ya = v1.vertex.y;
float xb = v2.vertex.x; float yb = v2.vertex.y;
float xc = v3.vertex.x; float yc = v3.vertex.y;
float x = pixel.x; float y = pixel.y;
float gamma = ((ya - yb) * x + (xb - xa) * y + xa * yb - xb * ya) /
((ya - yb) * xc + (xb - xa) * yc + xa * yb - xb * ya);
float beta = ((ya - yc) * x + (xc - xa) * y + xa * yc - xc * ya) /
((ya - yc) * xb + (xc - xa) * yb + xa * yc - xc * ya);
float alpha = 1 - beta - gamma;
return v1 * alpha + v2 * beta + v3 * gamma;
}
这样还差最后一步,就是透视矫正。
重心坐标下的透视矫正插值
我们之前讨论的是2D空间下的透视矫正,用于处理EdgeWalking中两次线性插值的情况算是刚好合适,但是现在我们处理的是重心坐标插值,那么我们该怎么计算重心坐标在透视投影前后的alpha,beta与gamma之间的关系呢?
我们再来深入浅出一下透视投影发生了什么:
简化一下公式
现在我们假设一个点P(x, y, z)和一个三角形,顶点为ABC,则满足重心坐标方程:
方程两边左乘透视矩阵:
我们将这些向量从第三行“切”开,变成两个方程:
直接把下面那个式子代入上边:
这样我们透视后的alpha、beta和gamma值与透视前的alpha、beta和gamma的关系就出来了
直接开写:
Vertex barycentricPerspectiveLerp(const Triangle& t, const myEigen::Vector2f& pixel
, const std::array<myEigen::Vector4f, 3>& v)
{
Vertex v1 = t.vertex[0]; Vertex v2 = t.vertex[1]; Vertex v3 = t.vertex[2];
float xa = v1.vertex.x; float ya = v1.vertex.y;
float xb = v2.vertex.x; float yb = v2.vertex.y;
float xc = v3.vertex.x; float yc = v3.vertex.y;
float x = pixel.x; float y = pixel.y;
float g = ((ya - yb) * x + (xb - xa) * y + xa * yb - xb * ya) /
((ya - yb) * xc + (xb - xa) * yc + xa * yb - xb * ya);
float b = ((ya - yc) * x + (xc - xa) * y + xa * yc - xc * ya) /
((ya - yc) * xb + (xc - xa) * yb + xa * yc - xc * ya);
float a = 1 - b - g;
float W = 1.0f / (a / v[0].w + b / v[1].w + g / v[2].w);
float beta = (b / v[1].w) * W;
float gamma = (g / v[2].w)* W;
float alpha = 1.0f - beta - gamma;
return v1 * alpha + v2 * beta + v3 * gamma;
}
输出结果:
一模一样,但是同样是72帧花了8秒往上,显然对于单线程CPU来说这个算法更慢,而对于高度并行的GPU来说,这种逻辑简单,计算归结到每个像素内的算法显然比先给三角形一分为二,再用扫描线移动的EdgeWalking更加合适。
深度测试
目前为止我们只是对于一个三角形进行操作,一旦有多个三角形,我们就不得不思考一下遮挡关系的问题了。
一般来说深度测试在着色阶段的后面,可能会有点奇怪,如果先深度测试再着色不就能避免很多overdraw的问题了吗?
能避免,但也会带来其他问题。渲染效率上提升幅度确实很大,但是涉及到透明物体渲染,或者着色阶段的fragment shader编写中更改了深度信息,那么我们先进行深度测试就会导致渲染出错误的图像。
但是确实先做深度测试能带来渲染效率上的大提升,所以GPU硬件中已经集成了early-z的算法,可选择开启与否。
画家算法与其局限性
画家算法就像他的名字一样好理解,怎么画出三角形的遮挡关系?答:从远及近给三角形排个序,先画远的再画近的。
看似粗暴,但是真的有用。但是对于一些复杂遮挡关系就没辙,比如下图:
你说这种怎么给三角形排个先后画的顺序呢?
而且传统的算法中对于三角形的前后排序涉及到空间分割的数据结构,一般是使用BSP树对三角形排序,对于三角形相互穿过的情况进行裁剪,但如果场景很大,或者物体动的很快的情形就不适用,即使是BSP树也会显得很慢,在如今我们无论是软光栅还是硬光栅,普遍使用的方法就是Z-Buffer。
Z-Buffer
Z-Buffer说起来非常简单,创建一个Buffer来存储每个像素的深度值,当某个像素被覆盖时,将会与Z-Buffer里存储的当前像素已有深度值进行测试,如果离摄像机更近则覆盖上去,更远就什么也不做。
我们直接写一下代码,其实可以直接参考下tgaimage里data这个类似帧缓冲的实现:
rasterizer::rasterizer(const std::string& f, const TGAImage& img)
:filename(f), image(img), width(img.width()), height(img.height()),
zneardis(0.1f), zfardis(50), fovY(45), aspect(1)
{
...
z_buffer.resize(img.width() * img.height());
std::fill(z_buffer.begin(), z_buffer.end(), -std::numeric_limits<float>::infinity());
}
int rasterizer::get_index(int x, int y)
{
return y * width + x;
}
void rasterizer::rasterize_edge_equation(const Triangle& m, const std::array<myEigen::Vector4f, 3>& clipSpacePos)
{
...
Vertex pixel = barycentricPerspectiveLerp(m, myEigen::Vector2f(x + 0.5, y + 0.5), clipSpacePos);
if (pixel.vertex.z > z_buffer[get_index(x, y)])
{
image.set(x, y, pixel.vertexColor);
z_buffer[get_index(x, y)] = pixel.vertex.z;
}
}
EdgeEquation中的实现就是这样,EdgeWalking中的实现其实也一模一样,根本没几行代码的事。
看看结果(EdgeWalking):
我传入的三角形是games101作业2中的三角形数据,传入顺序是先传前面的三角形,再传后面的三角形,但是结果依然给出了正确的遮挡关系,说明深度测试正确起效果了。
结语
这一节很多内容比我想象的难一点,稍微做的晚了一些,而且依然有点缺憾,我后面也许会再出几篇文章补充一下。
首先是齐次坐标裁剪,我们并没有实现完整的齐次坐标裁剪,而是将其一部分工作转移到了屏幕空间进行,Cohen-Sutherland算法应该是完全可以拓展到3维或者4维的,这一点我写的时候没有考虑清楚,后续会再出一篇文章详细讲讲齐次坐标裁剪。
然后是深度测试的精度问题,我们忽略掉了很多事情,真正的Zbuffer储存在GPU上不同位数会有迥异的表现,而且我们处理的深度值没有做过任何变换,直接传入了原始的NDC坐标,会触及到一些浮点数精度之类的问题,也许这个也可能会再出篇文章讲讲深度测试的精度。
当然还是先出下一节为主,下一节不出意外的话应该是做纹理映射,我们会提前引入一个读取obj文件的头文件,届时应该可以看看我们渲染器的表现如何了。