卷积神经网络及经典模型（3） 误差和优化器

构建好网络结构后就要开始训练了，对于一个模型来说，评估函数和代价函数可以说是模型的”眼睛“，因为通过评估函数可以量化模型的预测结果，通过代价函数可以量化模型预测结果的好坏，只有量化后才能使用优化器去优化模型。在分类问题中，softmax是常用的评估函数，对应的损失函数为交叉熵函数。

1. SoftMax函数

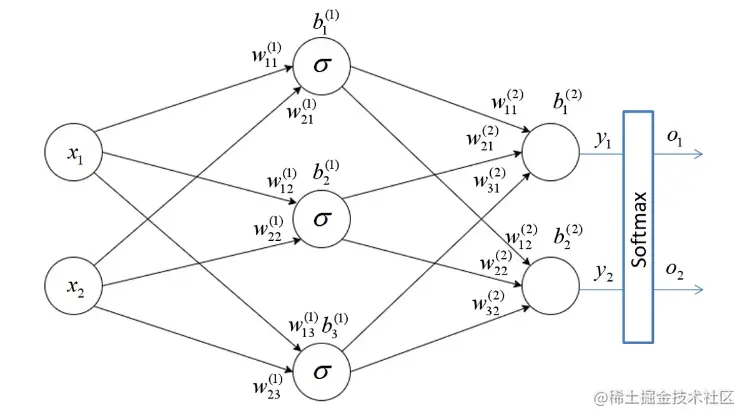
计算误差之前需要先进行前向传播得到输出，对于分类问题，也就代表每个类别的预测结果，如上图所示的一个神经网络，和普通神经网络不同的是，输出之前还经过了Softmax，经其好处是经过Softmax函数处理后的输出节点概率和为1，计算方法为$：\frac{e^{y_i}}{\sum_je^{y_i}}$,对于上面的网络，计算公式为$：O_1=\frac{e^{y_1}}{e^{y_1}+e^{y_2}}$ $：O_2=\frac{e^{y_2}}{e^{y_1}+e^{y_2}}$

2. 误差的计算

3. 权重的更新

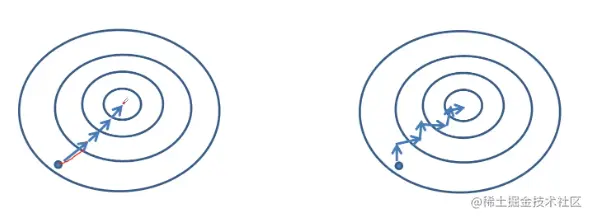
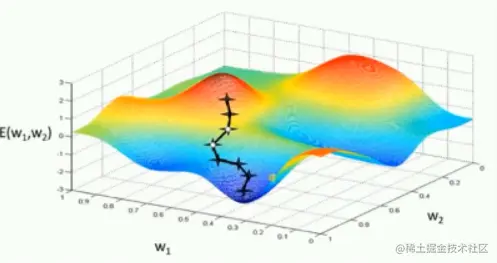
计算得到误差后，求偏导得到梯度即可进行反向传播，更新权重。但是这有一个问题，若使用整个样本集进行求解则损失梯度指向全局最优方向（如下图左），这是没问题的。但是在实际应用中往往不可能一次性将所有数据载入，内存(算力也不够)，比如lmageNet项目的数据库中有超过1400万的图像数据，所以只能分批次(batch)训练。若使用分批次样本进行求解，损失梯度指向当前批次最优方向（如下图右），这就有可能导致进入局部最优解。

SGD优化器

计算公式为：$\omega_{t+1}=\omega_t-\alpha·g(\omega_t)$，其中$\alpha$为学习率,  为t时刻对参数 $g(\omega_t)$ 的损失梯度，这就是最基础的优化器，其缺点在于易收到样本干扰，容易陷入局部最优解。

SGD+Momentum优化器

计算公式：

$\alpha$为学习率, $g(\omega_t)$为 t 时刻对参数 $w_t$ 的损失梯度 $\eta(0.9)$ 为动量系数

Adagrad优化器（自适应学习率）

计算公式：

$s_t=s_{t-1}+g(\omega_t){\cdot}g(w_t)$

$\omega_{t+1}=\omega_t-\frac{\alpha}{\sqrt{s_i+\epsilon}}{\cdot}g(w_t)$

 $\alpha$为学习率, $g(w_i)$ 为 t 时刻对参数 $w_i$ 的损失梯度 $\epsilon(10^{-7})$ 为防止分母为零的小数，其缺点在于学习率下载太快，可能没收敛就停止训练了。

RMSProp优化器（自适应学习率）

计算公式：

$s_t=\eta{\cdot}s_{t-1}+(1-\eta){\cdot}g(w_t)$

$w_{t+1}=w_t-\frac{\alpha}{\sqrt{s_t+\epsilon}}{\cdot}g(w_t)$

$\alpha$为学习率, $g(w_t)$ 为 t 时刻对参数 $w_t$ 的损失梯度$\eta(0.9)$控制衰减速度, $\epsilon(10^{-7})$ 为防止分母为零的小数.

Adam优化器（自适应学习率）

$m_t=\beta_1{\cdot}m_{t-1}+(1-\beta_1){\cdot}g(w_t)$

$v_t=\beta_2{\cdot}v_{t-1}+(1-\beta_2){\cdot}g(w_t){\cdot}g(w_t)$

$\hat{m_t}=\frac{m_t}{1-\beta^t_1}$ $\hat{v_t}=\frac{v_t}{1-\beta^t_2}$

$w_{t+1}=w_t-\frac{\alpha}{\sqrt{\hat{v_t}+\epsilon}}\hat{m_t}$

$\alpha$为学习率, $g(w_t)$ 为 t 时刻对参数 $w_t$ 的损失梯度 $\beta_1(0.9)$、$\beta_2(0.999)$控制衰减速度，$\epsilon(10^{-7})$ 为防止分母为零的小数.

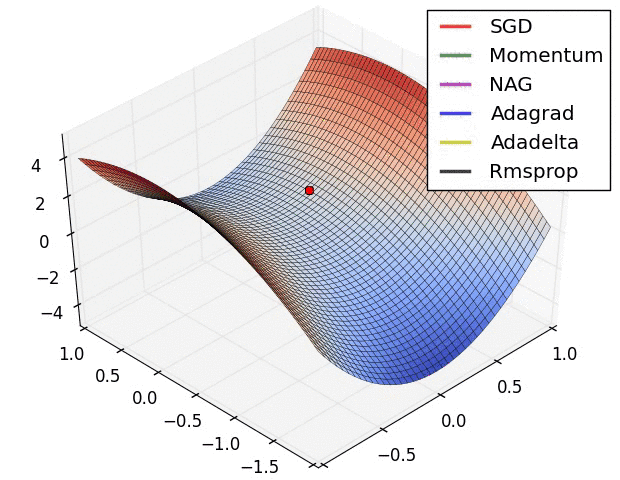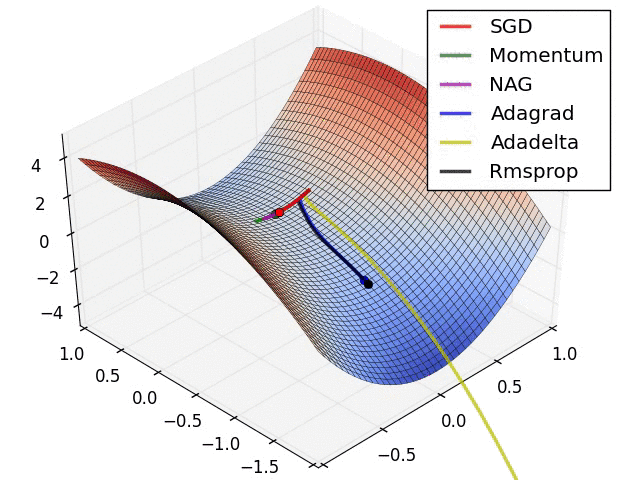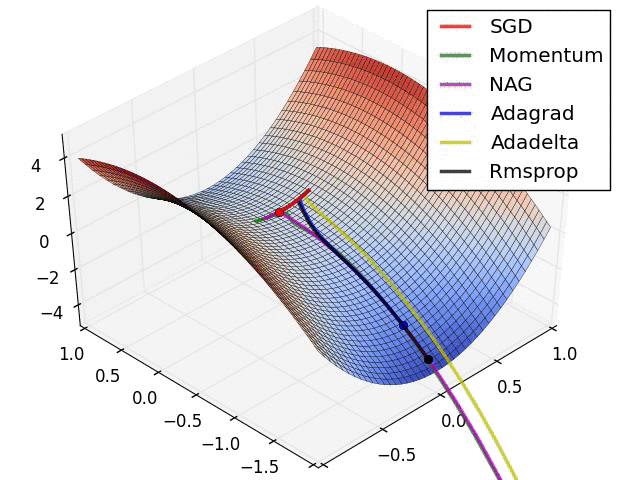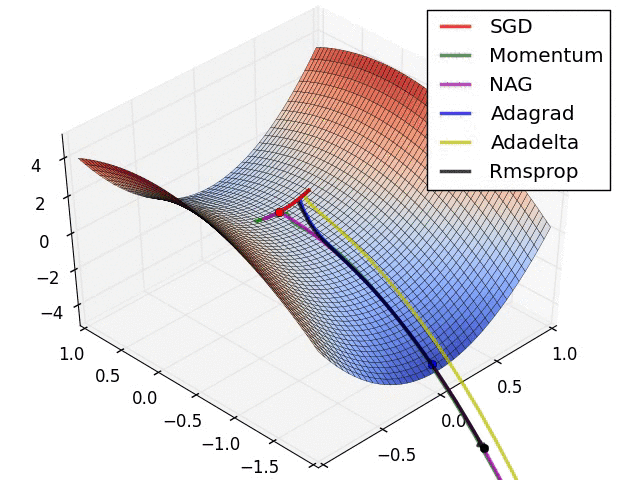
下图是不同优化器寻找最优解的动画。