好吧, 说实在的, 我是没学懂这节课啦, o(TヘTo) 就当做做笔记啦
神经模型
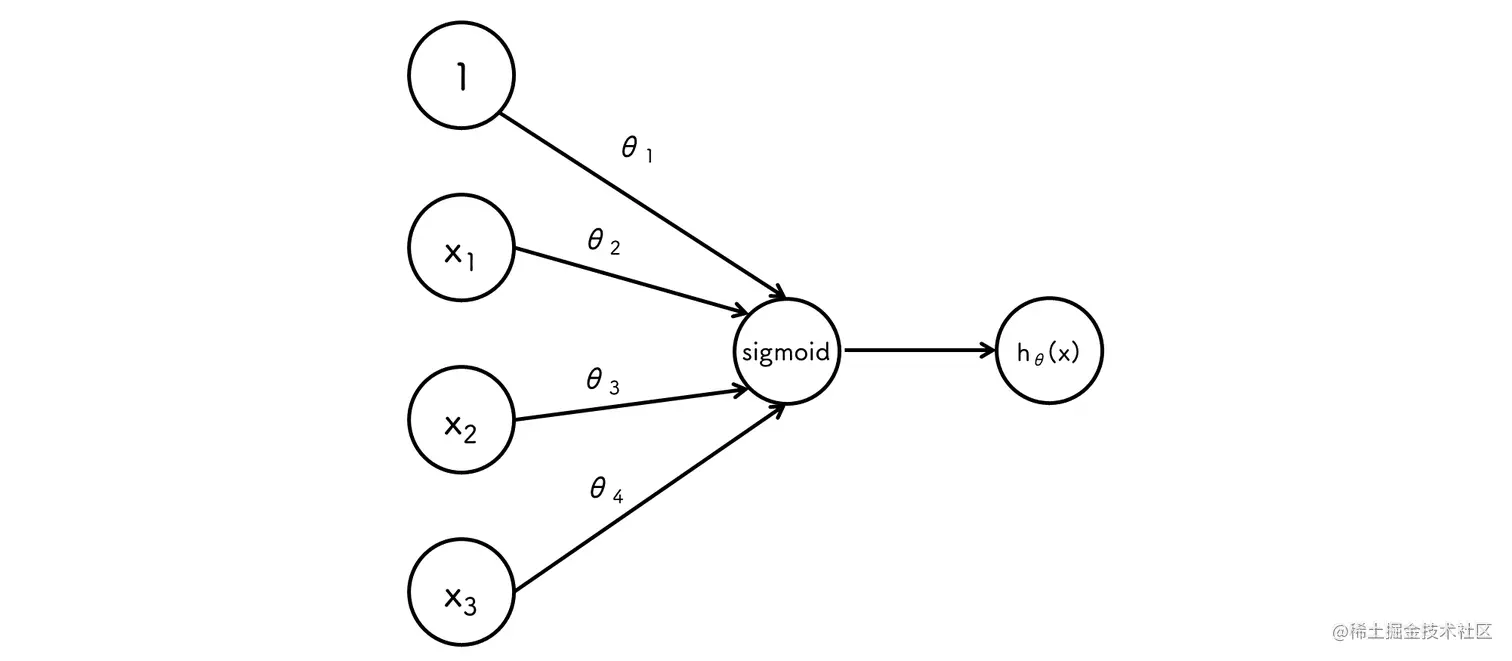
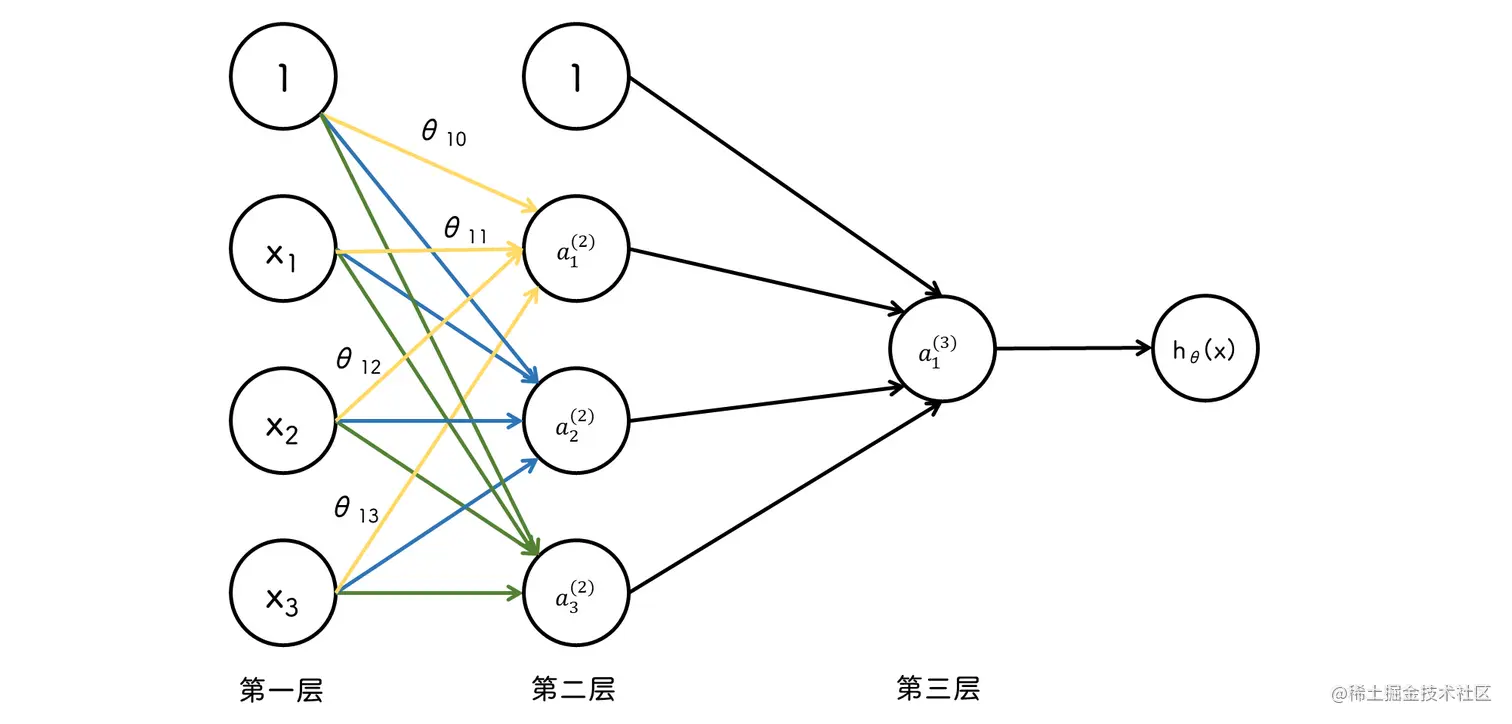
a1(2)=h(θ10(1)x0+θ11(1)x1+θ12(1)x2+θ13(1)x3)
a2(2)=h(θ20(1)x0+θ21(1)x1+θ22(1)x2+θ23(1)x3)
a3(2)=h(θ30(1)x0+θ31(1)x1+θ32(1)x2+θ33(1)x3)
hθ(x)=a1(3)=h(θ10(2)a0(2)+θ11(2)a1(2)+θ12(2)a2(2)+θ13(2)a3(2))
右上角的 (2) 代表第二层
此时可以令 z1(2)=Θ10(1)x0+⋯ , 即 z1(2)=Θ(1)a(1)
那么就有 a1(2)=h(z1(2))
X = [ones(m, 1) X];
a2 = sigmoid(X * Theta1');
a2 = [ones(m, 1) a2];
h = sigmoid(a2 * Theta2');
[~, p] = max(h, [], 2);
感知器示例
y^={10h≥0.5h<0.5
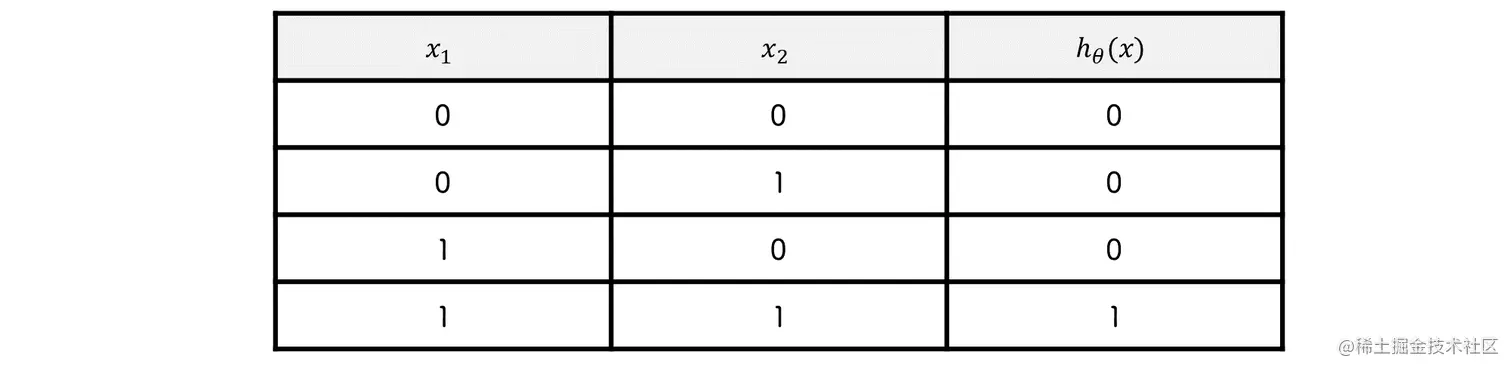
逻辑与
hθ(x)=sigmoid(x1+x2−1.5)
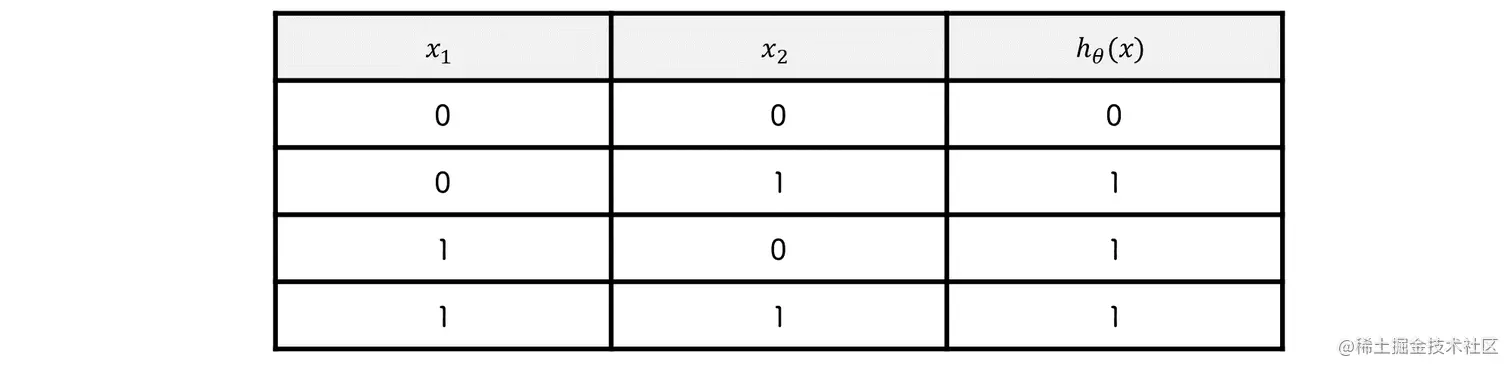
逻辑或
hθ(x)=sigmoid(x1+x2−0.5)
逻辑非
hθ(x)=sigmoid(−x1+0.5)

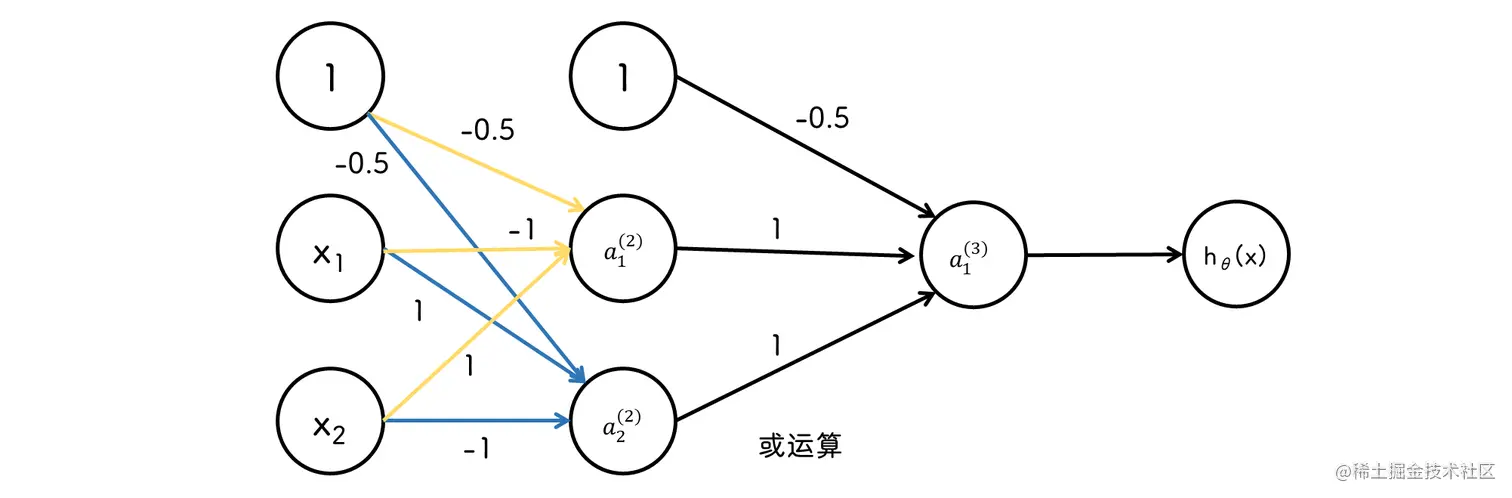
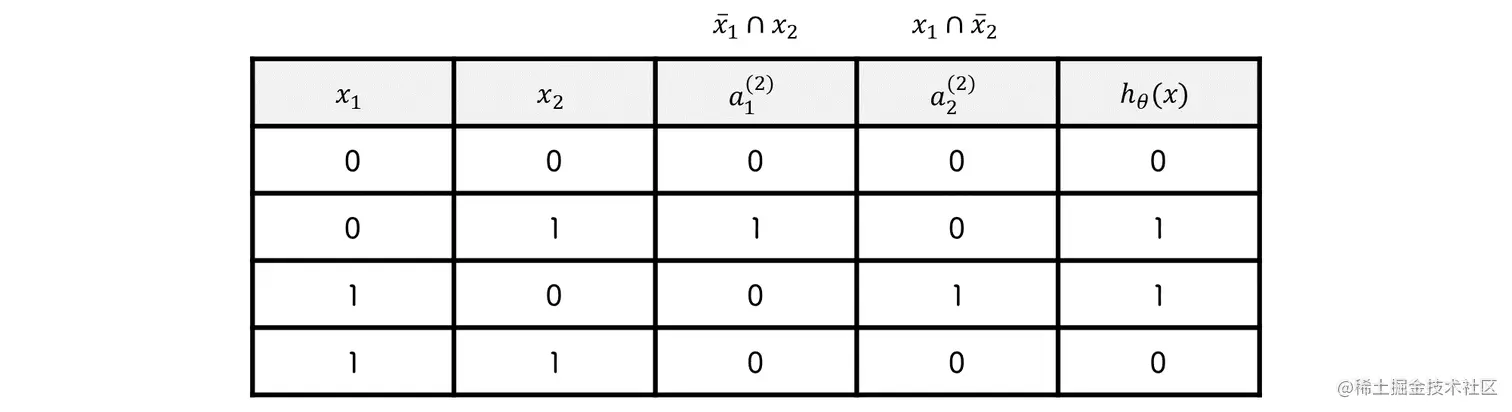
异或
y=x1⊕x2=(x1∩x2)∪(x1∩x2)
代价函数
logistic 回归的代价函数:
J(θ)=−m1i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))+2mλj=1∑nθj2
神经网络的代价函数
J(θ)=−m1i=1∑mk=1∑K(yk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−hΘ(x(i))))+2mλl=1∑L−1i=1∑slj=1∑sl+1(θji(l))2
其中 K 代表第几层, 正则项为从第一层到 L-1 层
X = [ones(m, 1) X];
a1 = X;
z2 = a1 * Theta1';
a2 = [ones(m, 1) sigmoid(z2)];
z3 = a2 * Theta2';
a3 = sigmoid(z3);
I = eye(num_labels);
Y = I(y,:);
re = (sum(sum(Theta1(:, 2:end).^2)) + ...
sum(sum(Theta2(:, 2:end).^2))) ...
* lambda / 2 / m;
J = -sum(sum((Y .* log(a3) + (1 - Y) ...
.* log(1 - a3)))) / m +re;
BP算法
全称 BackPropagation (反向传播算法)
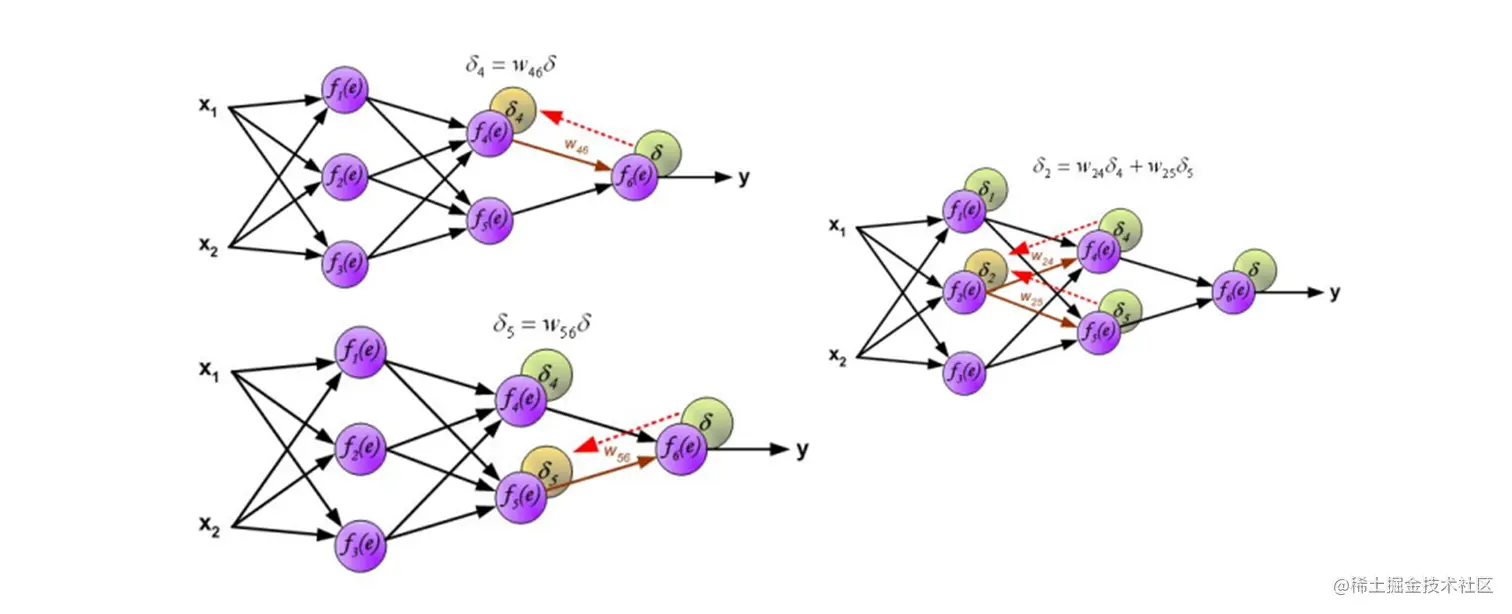
最终层的误差如何分解到各个节点的输出上?
根据 权重 一层层的往 前 分解
Sigmoid 梯度
sigmoid(z)=g(z)=1+e−z1
grad=g′(z)=g(z)(1−g(z))
g = sigmoid(z) .* (1 - sigmoid(z));
梯度
已知 z(i+1)=θ(i)a(i)
令误差为
δ(4)=∂a(4)∂z(4)∂J∂a(4)
δ(3)=∂a(4)∂z(4)∂a(3)∂z(3)∂J∂a(4)∂z(4)∂a(3)
那么梯度为
∂Θ(2)∂J=∂a(4)∂z(4)∂a(3)∂z(3)∂J∂a(4)∂z(4)∂a(3)⋅∂Θ(2)∂z(3)
梯度下降法计算 Θ :
Θij(2)(t+1)=Θij(2)(t)−α×∂Θij(2)∂J
已知
∂a(4)∂J=a(4)(1−a(4))a(4)−y
∂z(4)∂a(4)=a(4)(1−a(4))
因此
δ(4)=∂a(4)∂z(4)∂J∂a(4)=a(4)−y
其中 a(i)=h(z(i))
同理, 已知 z(4)=Θ(3)a(3), 即
∂a(3)∂z(4)=Θ(3)
那么
δ(3)=∂a(4)∂z(4)∂J∂a(4)⋅∂z(3)∂z(4)⋅∂z(3)∂a(3)=δ(4)⋅Θ(3)⋅h′(z(3))
同理
δ(2)=δ(3)⋅Θ(2)⋅h′(z(2))
delta3 = a3 - Y;
dt = delta3 * Theta2;
delta2 = dt(:, 2:end) .* sigmoidGradient(z2);
梯度为
∂Θ(3)∂J=δ(4)⋅a(3)
∂Θ(2)∂J=δ(3)⋅a(2)
∂Θ(1)∂J=δ(2)⋅a(1)
梯度下降
Δij(l)=Δij(l)+δj(l+1)ai(l)
Delta1 = delta2' * a1;
Delta2 = delta3' * a2;
正则化
∂Θij(l)∂J=⎩⎨⎧m1Δij(l)+mλθij(l)m1Δij(l)j>0j=0
Theta1_grad = Delta1 / m + lambda * ...
[zeros(hidden_layer_size , 1) Theta1(:, 2:end)] / m;
Theta2_grad = Delta2 / m + lambda * ...
[zeros(num_labels , 1) Theta2(:, 2:end)] / m;
grad = [Theta1_grad(:) ; Theta2_grad(:)];