Ch4 串 | 数据结构第 4 章串 4.1 串的概念和基本操作 4.1.1 串的概念和基本术语 s 是串名，用引号引

第 4 章串

4.1 串的概念和基本操作

4.1.1 串的概念和基本术语

s = "a1a2...an" (n >= 0)

s 是串名，用引号引起来的字符序列是串的值，ai 可以是字母、数字、空格、其他字符。引号本身不属于串的内容。ai (1<=i<=n) 是一个任意字符，它称为串的元素，是构成串的基本单位，i 是它在整个串中的序号。
n 为串的长度，表示串中所包含的字符个数，当 n=0 时，称为空串，通常记为 $\phi$ 。

子串和主串：串中任意个连续的字符组成的子序列称为该串的子串。包含子串的串称为主串。

串相等：两个串长度相等，且对应位置的字符都相等。

空串和空白串：空串不包含任何字符，表示为 $\phi$ ；空白串由一个或多个空格组成，如 ' ' 。

子串的位置：子串的第一个字符在主串中的序号称为子串的位置。

例：主串 abcdpqrst 中 cdp 子串在主串中的位置为 3

4.1.2 串的基本操作

(1) 串赋值

用串常量赋值

StrAssign(&T, chars) //生成一个值等于chars的串T

用串变量赋值

StrCopy(&T, S)

(2) 判定空串

StrEmpty(S)

(3) 两串比较

StrCompare(S, T)

若 S > T ，返回值 > 0 ，若 S = T，返回值 = 0，若 S < T ，返回值 < 0

(4) 求串长

StrLength(S)

(5) 串清空

ClearString(&S)

(6) 两串连接

Concat(&T, S1, S2)

用 T 返回由 S1 和 S2 联接而成的新串

(7) 求子串

SubString(&Sub, S, pos, len)

用 Sub 返回串 S 第 pos 个字符起长度为 len 的子串

(8) 子串定位

Index(S, T, pos)

返回主串 S 中从 pos 开始的部分存在值和 T 相同的子串，则返回 pos 开始后第一次出现的位置，否则返回 0

(9) 子串置换

Replace(&S, T, V)

用 V 替换主串 S 中出现的所有与 T 相等的不重叠子串

(10) 插入子串

StrInsert(&S, pos, T)

在 pos 位置前插入 T

(11) 删除子串

StrDelete(&S, pos, len)

(12) 串销毁

DestroyString(&S)

串的操作举例：

设：
	s=‘I am a student.’
	t=‘OK!’
	p=‘student’
	q=‘nurse’
	r=‘good ’

(1) Concat (l, s, t)
	l = ‘I am a student.OK!’

(2) Replace(s, p , q);
	s=‘I am a nurse.’

(3) StrInsert(s, 8, r)
	s=‘I am a good nurse.’

4.2 串的表示和实现

4.2.1 定长顺序存储表示

用一组地址连续的存储单元存储串值中的字符序列，可以定长来指明最大的字符个数，也叫定长串。如：

#define MAXSIZE 256 
char s[MAXSIZE]; //字符串中的字符个数不能超过256

三种标识串实际长度的方法

类似顺序表，用一个变量 curlen 来指向最后一个字符的存储下标，这种方式可以直接得到串的长度：s.curlen + 1
在串尾存储一个特殊字符来作为终结符
用 s[0] 存放串的实际长度，串值存放在 s[1] ~ s[MAXSIZE-1]

Pasted image 20221006105938.png

基本操作实现示例（方式三）

#define MAXSTRLEN 255 //预定义最大串长
typedef unsigned char SString[MAXSTRLEN + 1];

操作基于字符序列复制

约定：串值长度上溢时，用 “截尾法” 处理，即 “截断” 超过予定义长度的部分。

两串连接：

Status Concat(SString  &T,  SString S1, SString S2)
//用T返回串s1和s2联接而成的新串。
//uncut表示是否截断，未截断TRUE，截断为FALSE
{   
	if  ( S1[0] + S2[0] <= MAXSTRLEN ) {
		T[1 ... S1[0]] = S1[1 ... S1[0]];
		T[S1[0] + 1 ... S1[0] + S2[0]] = S2[1 ... S2[0]];
		T[0] = S1[0] + S2[0];
		uncut = TRUE;
	} else if (S1[0] < MAXSTRLEN) {
		T[1 ... S1[0]] = S1[1 ... S1[0]];
		T[s1[0] + 1 ... MAXSTRLEN] = S2[1 ... MAXSTRLEN - S1[0]];
		T[0] = MAXSTRLEN;
		uncut = FALSE;
	} else  {
		T[0 ... MAXSTRLEN] = S1[0 ... MAXSTRLEN];  
		uncut = FALSE;
	}
	return uncut;
} // Concat

求子串：

Status SubString(SString &Sub, SString S, int pos, int len)
//用Sub返回串S从第pos个字符起长度为len的子串
{
	if (pos < 1 || pos > S[0]  || len < 0  || len > S[0] - pos + 1)
		return ERROR;
	Sub[1 ... len]= S[pos ... pos + len - 1];
	Sub[0] = len;
	return OK;
} // SubString

两串比较：

int StrCompare(SString S, SString T)
// S>T,返回值>0；S=T，返回0；S<T，返回值< 0
{     
	for (i = 1; i <= S[0] && i <= T[0]; i++) {//逐个字符进行比较
		if (S[i] != T[i])
		return(S[i] - T[i]);
	}
	return S[0] - T[0];
} // StrCompare

4.2.2 堆分配存储表示

动态分配串值存储空间，避免定长结构的截断现象。

typedef struct {
	char *ch; //串空间基址，按串长申请
	int length; //串长度
} HString;

基本操作实现实例

两串比较：

int StrCompare(HString  S, HString T)
 //S>T,返回值>0；S=T，返回0；S<T，返回值< 0
{    
for (i = 0; i < S.length && i < T.length; i++) {
	if (S.ch[i] != T.ch[i])
		return S.ch[i] - T.ch[i];
}
	return  S.length - T.length;
} // StrCompare

两串连接：

Status Concat(HString &T,  HString  S1, HString S2)
//返回串S1和S2联接而成的新串T
{
	if (T.ch) free(T.ch);   //释放T原有空间
	if (!(T.ch = (char *)malloc((S1.length + S2.length)*sizeof(char))))
		exit(OVERFLOW);
	T.length = S1.length + S2.length;
	T.ch[0 ... S1.length - 1] = S1.ch[0 ... S1.length - 1];
	T.ch[S1.length ... T.length - 1] = S2.ch[0 ... S2.length - 1];
	return OK;
} // Concat

求子串：

Status SubString(HString &Sub, HString S, int pos, int len)
//求串S从第pos个字符起长度为len的子串Sub
{    
	if (pos < 1 || pos > S.length || len < 0 || len > S.length - pos + 1)
		return ERROR;
	if (Sub.ch)  free(Sub.ch);
	if (!len) {
		Sub.ch = NULL;  Sub.length=0;
	} else {
		if (!(Sub.ch = (char *)malloc(len * sizeof(char))))
			exit(OVERFLOW);
		Sub.ch[0 ... len - 1] = S.ch[pos - 1 ... pos + len - 2];
		Sub.length = len;
	}
	return OK; 
} // SubString

4.2.3 块链存储表示

Pasted image 20221006161321.png

#define CHUNKSIZE 4         //由用户定义块大小
typedef struct Chunk {
	char ch[CHUNKSIZE];
	struct Chunk *next;
} Chunk;
typedef struct {
	Chunk *head, *tail;     //串的、尾头指针
	int curlen;             //串的当前长度
} LString;

存储密度 = \cfrac{串值所占的存储位}{实际分配的内存位}

占用空间，操作复杂。但灵活，可实现的功能丰富。

4.3 串的模式匹配

模式匹配的应用：

搜索引擎
文档检索

定义：

子串定位操作称为串的模式匹配

模式匹配函数：

Index(S, T, pos)

返回子串 T 在主串 S 中第 pos 个字符之后第一次出现的位置；不存在，返回 0

暴力算法（Brute Force）

穷举法

int StrIndex(SString S, SString T, int pos)
{
	i = pos; j = 1;  
	while (i <= S[0] && j <= T[0]) { 
		if (S[i] == T[j]) {
			++i;
			++j;
		}// 继续比较后继字符 
		else {
			i = i - j + 2; 
			j = 1;
		} // 指针后退重新开始匹配
	}
	if (j > T[0])
		return i - T[0];
	else
		return 0; 
} // Index

算法性能分析

该匹配过程易于理解，且在某些应用场合，效率也较高，设串 s 长度为 n，串 t 长度为 m。
在好的情况下，每趟不成功的匹配都发生在第一对字符比较时

例如： s =“aaaaaaaaaabc” t=“bc”
分析

设匹配成功发生在 Si 处，则在前面 i-1 趟匹配中共比较 i - 1 次，第 i 趟成功匹配时比较了 m 次，所以总共比较 i - 1 + m 次。

所有匹配成功的可能共有 n - m + 1 种，假设是等概率的，那么在 Si 匹配成功的概率是 pi = 1 / (n - m + 1) 。因此好的情况下的平均比较次数是：

$\sum\limits_{i=1}^{n-m+1}p_{i}\times (i-1+m)=\sum\limits_{i-1}^{n-m+1}=\cfrac{n+m}{2}$

即匹配成功的最好情况的时间复杂度为 $O(n+m)$
在最坏情况下，每趟不成功的匹配都发生在 t 的最后一个字符。

例如 s：“aaaaaaaaaaab”，t：“aaab”时
分析

设匹配成功发生在 Si 处，则在前面 i - 1 趟匹配中共比较（i - 1）* m 次，到第 i 趟成功匹配共比较 i * m 次。所有匹配成功的可能共有 n - m + 1 种，假设是等概率的。

$\sum\limits_{i=1}^{n-m+1}p_{i}\times (i\times m)=\sum\limits_{1}^{n-m+1}\times (i\times m)=\cfrac{m\times (n-m+2)}{2}$

可见算法在最坏情况下的时间复杂度为 $O(n \times m)$
时间复杂度高的原因

在主串中可能存在多个和模式串 “部分匹配” 的子串，因而引起指针 i 的多次回溯。
改进方法

不回溯，模式向右滑动尽量远

Pasted image 20221006164208.png

Pasted image 20221006164226.png

接下来介绍不回溯的 KMP 算法

KMP 算法

12-串1 KMP 串的模式匹配

引入 next 数组

Pasted image 20221010151758.png

求得模式的 next 函数后，匹配可如下进行：

假设以指针i和j分别指示主串和模式中正待比较的字符
令i的初值为pos，j的初值为1
如果匹配继续向后比较
如果不匹配，则 i 不变，j 退到 k=next(j) 位置再比较

//KMP
int Index_KMP(SString S, SString T, int pos)
{
	i = pos, j = 1;
	while (i <= S[0] && j <= T[0]) {
		if (j == 0 || S[i] == T[j]) { i++; j++ } //继续比较后继字符
		else j = next[j]; //模式串向右移动
	}
	if (j > T[0]) return i - T[0]; //匹配成功
	else return 0;
}

这种改进算法是D.E.Knuth、V.R.Pratt和J.H.Morris 同时发现的，因此人们称它为克努特—莫里斯—普拉特操作（简称为KMP算法）。此算法可以在O（n+m)的时间数量级上完成串的模式匹配操作。

每当一趟匹配过程中出现字符比较不等时，不需回溯i指针，而是利用已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的一段距离后，继续进行比较。

KMP 小结

简单模式匹配算法性能较低的根源

比到不相等时主串指针 i=i-j+2, 模式串指针j=1

主串指针回溯是不必要的
改进思路

主串指针i不回溯，模式串指针j也尽量不从1开始，尽量多跳过一些不必要的比较，设next[j] = k
k的计算

当j等于1时，k=0；否则分析j前面的部分，看有没有正序x位和倒序x位相同的情况，如果没有这种情况k=1，如果有多于一种，则k等于x的最大值+1
next函数的修正

设主串S为'aaabaaaab' ,模式串T为'aaaab',

根据上一条规则，计算next[j]

当i=4, j=4时，比较S[4] != T[4]，此时查next[j]，应该让j=3，即比较S[4]和T[3], 但是因为T[3]和T[4]是相等的，所以T[3]肯定也是不等于S[4]的，即这次比较也是不必要的

修正策略：当T[j]=T[next[j]]时需要，需要将next[j] 修正为next[next[j]]，依次类推

总结和思考

模式匹配定义
简单模式匹配算法
改进算法-KMP
思考
- 模式匹配中，如模式带有通配符该如何匹配？比如用 aaa??*b 作为模式，其中 ? 是任何字符，* 是任何长度的字符串，可能为空。
- Boyer-Moore算法：坏字符、好后缀，最好时间复杂度 $O(n/m)$
- Rabin-Karp：借助哈希
- 多模式匹配：Trie树（字典树）、AC自动机

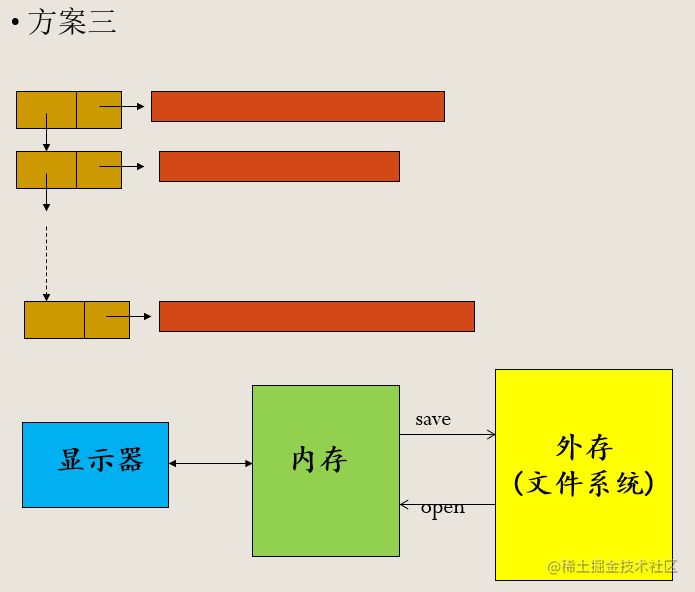
4.4 串应用示例--文本编辑

分析

操作对象
- 文本串（行是文本串的子串）
基本操作
- 查找
- 插入
- 删除

存储结构选择

方案一：简单顺序存储

Pasted image 20221010162125.png

方案二：

Pasted image 20221010162140.png

方案三：

![Pasted image 20221010162157.png](https://p1-juejin.byteimg.com/tos-cn-i-k3u1fbpfcp/7e53138713fe42afb39b8ddd36e2e519~tplv-k3u1fbpfcp-watermark.image?)

4.5 本章知识点小结

字符串线性结构的特点
字符串的顺序存储
字符串的链式存储
字符串的基本操作
模式匹配

Ch4 串 | 数据结构

第 4 章 串