回归

ARCTURUS
94 阅读3分钟

一元线性回归

判决函数

hθ=θ0+θ1xh_\theta = \theta_0 + \theta_1x

代价函数

使用代价(损失)函数评估训练数据与模型参数的匹配程度, 一列代表一个变量

J(θ0,θ1)=12m∑i=1m(hθ(xi1)−yi1)2J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})^2
% theta = [
%   theta0
%   theta1
% ]
J = (X * theta - y)' * (X * theta - y) / m / 2;

m 是样本数, 代价函数实际上为 误差平方和 , 而训练过程就是要实现

min(J)min(J)

最小化代价函数

解析求导法

求得最优参数只需要一步

损失函数是拟合参数 θ 的二次函数

J(θ)=aθ2+bθ+cJ(\theta) = a\theta^2+b\theta+c

通过求导并令导数等于 0 获取最小值

∂J(θ)∂θi=∂∂θi(12m∑i=1m(hθ(xi1)−yi1)2)=1m∑i=1m(hθ(xi1)−yi1)⋅xi1=0\begin{aligned} \frac{\partial J(\theta)}{\partial\theta_i} &=\frac{\partial}{\partial\theta_i}\left(\frac{1}{2m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})^2\right) \\ &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})·x_{i1} \\ &=0 \end{aligned}

解得

θ=(XTX)−1XTy\theta=(X^TX)^{-1}X^Ty

梯度下降法

计算一个函数的最小值, 可以从一个初始点, 朝着梯度下降的方向计算

θ0=θ0−αm∑i=1m(hθ(xi1)−yi1)\theta_0 = \theta_0 - \frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})
θ1=θ1−αm∑i=1m(hθ(xi1)−yi1)⋅xi1\theta_1 = \theta_1 - \frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})·x_{i1}

负梯度 为

−∂J(θ)∂θi=−αm∑i=1m(hθ(xi1)−yi1)⋅xi1-\frac{\partial J(\theta)}{\partial\theta_i}=-\frac{\alpha}{m}\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})·x_{i1}

α 为下降速度(步长), θ0\theta_0 的 x=1x=1 , 因此不存在末尾的 xx

num_iters = 1000;

m = length(y);
J_history = zeros(num_iters, 1); % 保存每次迭代时的代价

for iter = 1:num_iters % 共 1000 次迭代
  for j = 1:length(theta)
     % 这里也适用于多元的情况
     theta(j) = theta(j) - alpha / m * (X * theta - y)' * X(:, j);
  end
  
  J_history(iter) = computeCost(X, y, theta); 
 
end

得到了拟合参数 θ 后就可以进行预测了

predict = [1, 3.5] * theta;

多元线性回归

各维相互独立, 可以分别计算

判决函数

hθ(x)=θ0+θ1x1+⋯+θnxnh_\theta(x) = \theta_0 + \theta_1x_1 + \cdots + \theta_nx_n

代价函数

J(θ)=12m∑i=1m(h(xi.)−yi.)2J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h(x_{i.}) - y_{i.})^2

当变量间相差多个数量级时, 应该进行 归一化 , 这样才能收敛更快

[m, n] = size(X);
X_norm = zeros(m, n);

mu = mean(X); 
sigma = std(X); 

for i = 1:n 
  X_norm(:, i) = (X(:, i) - mu(i)) / sigma(i); 
end

Logistic 回归

分类与回归

  • 分类 hθ(x)∈{0,1}h_\theta(x)\in\{0,1\}, 0 代表负例, 1 代表正例
  • 回归 hθ(x)∈Rh_\theta(x)\in R

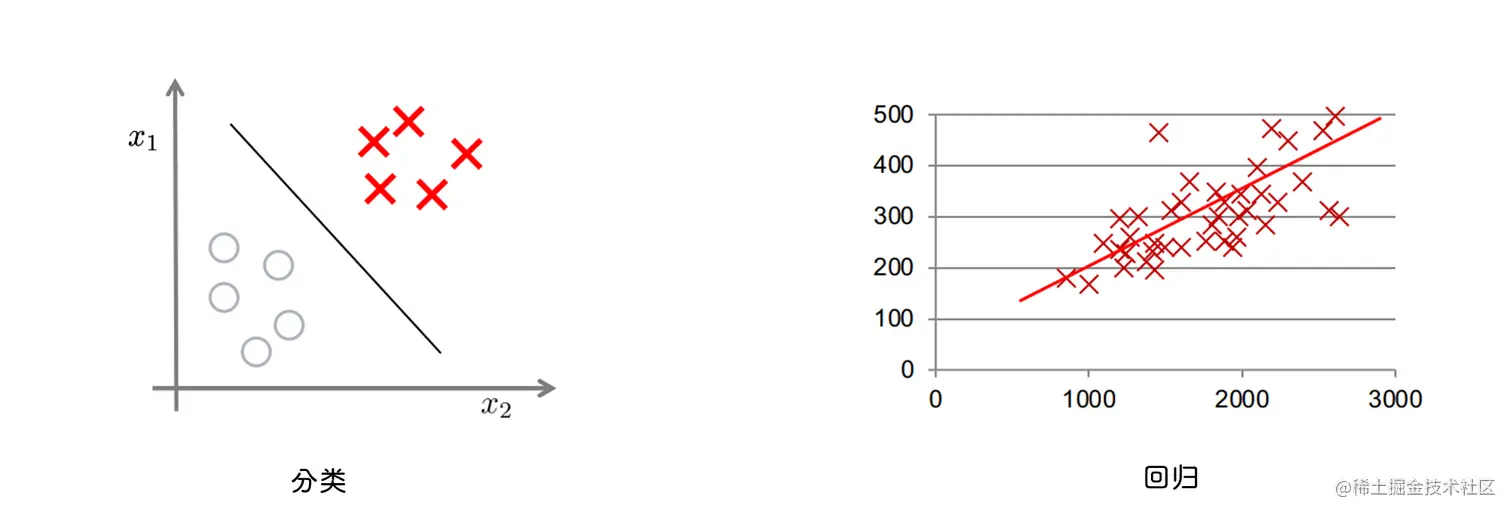
image.png

sigmoid 函数

将输出变到 0 或 1 附近

S(x)=11+e−xS(x)=\frac{1}{1+e^{-x}}

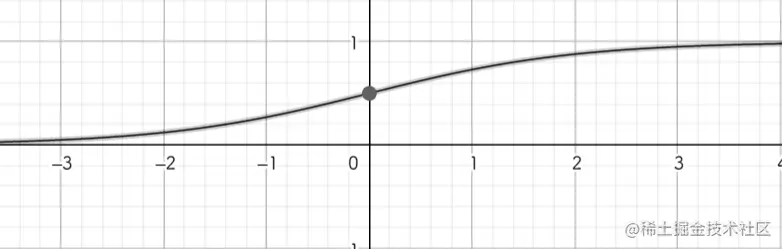
image.png

S′(x)=e−x(1+e−x)2=S(x)⋅(1−S(x))S'(x)=\frac{e^{-x}}{(1+e^{-x})^2}=S(x)·(1-S(x))
function g = sigmoid(z)

g = 1 ./ (1 + exp(-z)); % z 可以是矩阵

end

判决函数

hθ(x)=S(θx)=S(θ0+θ1x1+⋯ )=(1+e−θx)−1h_\theta(x) = S(\theta x) = S(\theta_0 + \theta_1x_1 + \cdots)=\left(1+e^{-\theta x}\right)^{-1}
  • 对于正例, 有 hθ(x)≥0.5 h_\theta(x) \ge 0.5 , θx≥0\theta x \ge 0
  • 对于负例, 有 hθ(x)<0.5 h_\theta(x) \lt 0.5 , θx<0\theta x \lt 0

根据已知的正负例计算出 θ

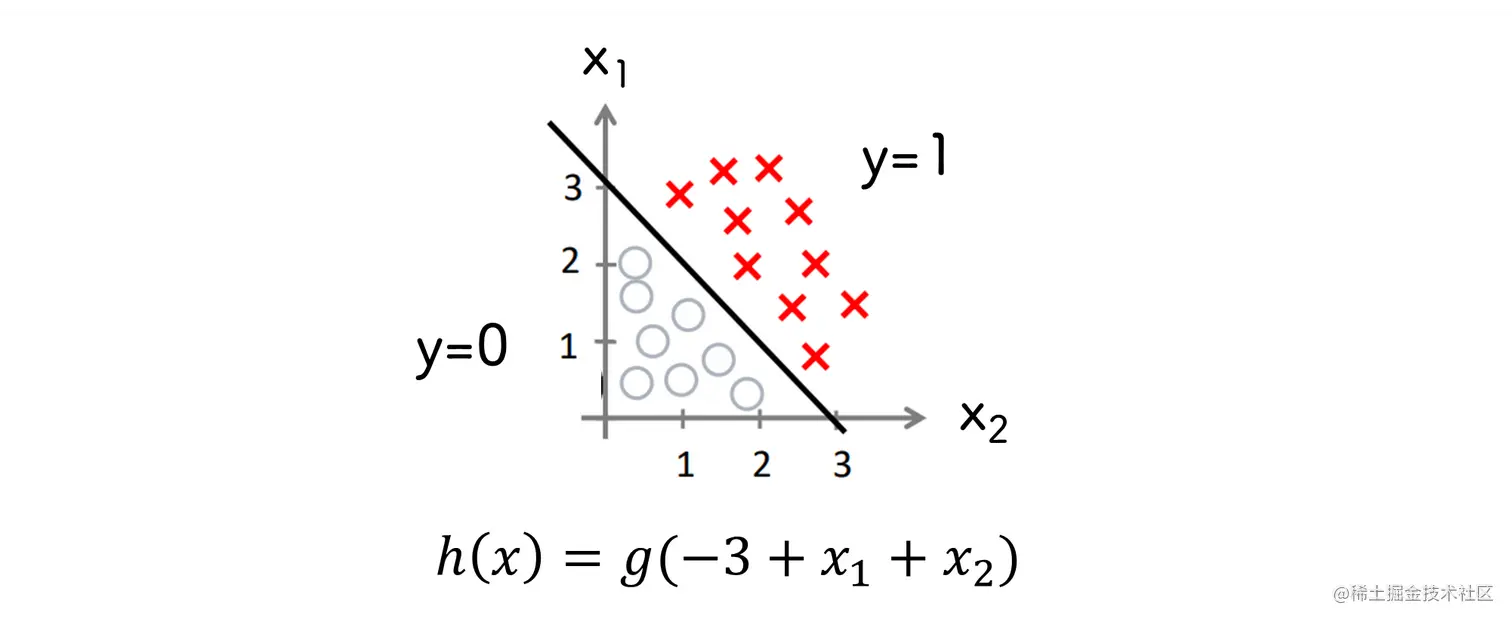
image.png

上图中

  • 正例 −3+x1+x2≥0-3+x_1+x_2\ge0
  • 负例 −3+x1+x2<0-3+x_1+x_2\lt0

代价函数

cost(hθ(x),y)={−log(hθ(x))y=1−log(1−hθ(x))y=0cost(h_\theta(x), y) = \begin{cases} -log(h_\theta(x)) & y = 1 \\ -log(1-h_\theta(x)) & y = 0 \\ \end{cases}

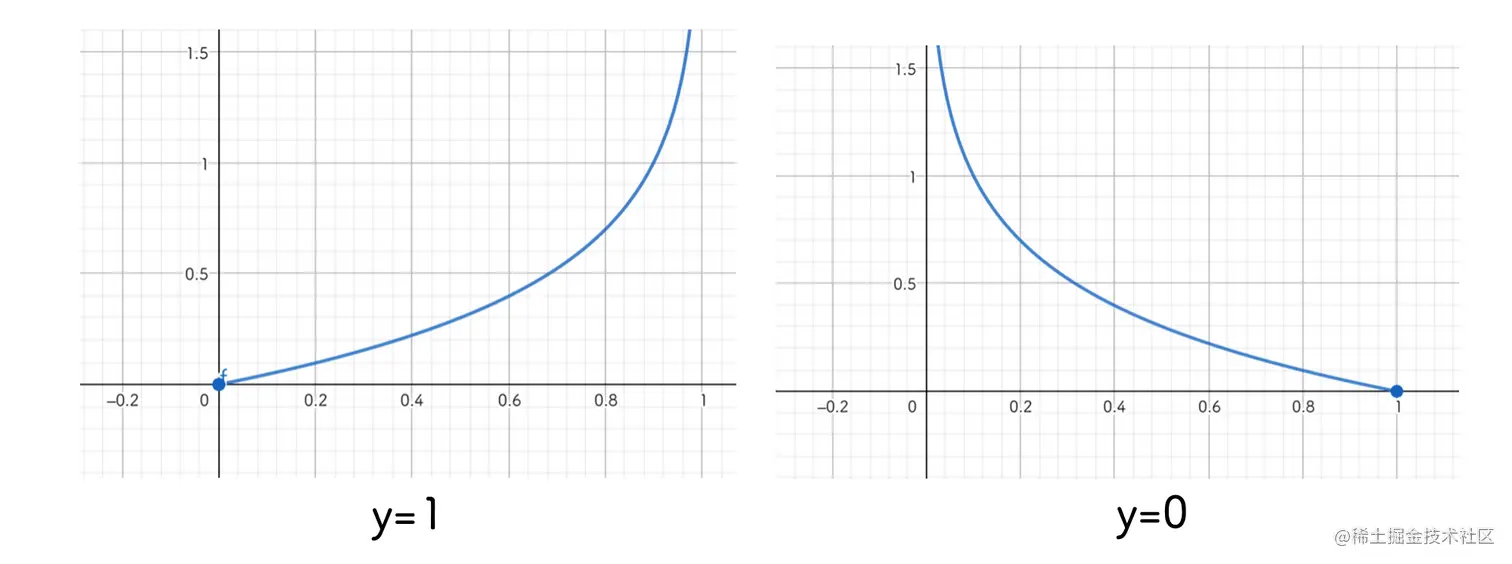
image.png

J(θ)=1m∑i=1mcost(hθ(xi),yi)=−1m∑i=1m[yi1log(hθ(xi1))+(1−yi1)log(1−hθ(xi1))]\begin{aligned} J(\theta) &= \frac{1}{m}\sum_{i=1}^mcost(h_\theta(x_i), y_i) \\ &= -\frac{1}{m} \sum_{i=1}^m \left[y_{i1}log(h_\theta(x_{i1}))+(1-y_{i1})log(1-h_\theta(x_{i1}))\right] \end{aligned}
h = sigmoid(X * theta);
J = - (y' * log(h) + (1 - y)' * log(1 - h)) / m;

精度评估

使用获得的拟合参数计算分类值, 与真实的分类值做比较

p = zeros(m, 1); 
t = sigmoid(X * theta); 

for i = 1:m 
  if  t(i) >= 0.5 
    p(i) = 1; 
  else p(i) = 0; 
  end 
end

p = predict(theta, X); 

fprintf('训练精度: %f\n', mean(double(p == y)) * 100);

最小化代价函数

解析求导法

∂hθ(x)∂θ=∂∂θ(11+e−θx)=hθ(x)⋅(1−hθ(x))⋅x\frac{\partial h_\theta(x)}{\partial\theta}=\frac{\partial }{\partial\theta} \left( \frac{1}{1+e^{-\theta x}} \right) =h_\theta(x)·(1-h_\theta(x))·x

初始梯度为

∂J(θ)∂θi=1m∑i=1m(h(xi1)−yi1)⋅xi1=0\frac{\partial J(\theta)}{\partial\theta_i}=\frac{1}{m}\sum_{i=1}^m(h(x_{i1}) - y_{i1})·x_{i1} = 0

这个公式和一元线性回归的代价函数导数一模一样, 只是判决函数 h(x) 不一样

grad = X' * (h - y) / m;

梯度下降

θi=θi−α∑i=1m(hθ(xi1)−yi1)⋅xi1\theta_i = \theta_i - \alpha\sum_{i=1}^m(h_\theta(x_{i1}) - y_{i1})·x_{i1}

正规化 logistic 回归

特征映射

为了更好的拟合, 使用变量多项式的特征来拟合

mapFeature=[1x1x2x12x1x2x22x13⋮x1x25x26]mapFeature = \begin{bmatrix} 1 \\ x_1 \\ x_2 \\ x_1^2 \\ x_1x_2 \\ x_2^2 \\ x_1^3 \\ \vdots \\ x_1x_2^5 \\ x_2^6 \\ \end{bmatrix}
degree = 6; 

row = length(X1); 

% 1 + 2(x1+x2) + 3(x1^2+x1x2+x2^2) + 4 + ...
% 6 次方一共 28 维
col = (degree + 2) * (degree + 1) / 2; 

out = ones(row, col); 

c = 2; 
for i = 1:degree 
  for j = 0:i 
    out(:, c) = (X1.^(i-j)).*(X2.^j); 
    c = c + 1; 
  end
end

代价函数

J(θ)=−1m∑i=1m[yi1log(hθ(xi1))+(1−yi1)log(1−hθ(xi1))]+λ2m∑j=1mθj.2J(\theta) = -\frac{1}{m} \sum_{i=1}^m \left[y_{i1}log(h_\theta(x_{i1}))+(1-y_{i1})log(1-h_\theta(x_{i1}))\right] + \frac{\lambda}{2m}\sum_{j=1}^m\theta_{j.}^2
∂(J(θ))∂θj={1m∑i=1m(h(xi1)−yi1)⋅xi1j=01m∑i=1m(h(xi1)−yi1)⋅xi1+λmθjj≥1\frac{\partial(J(\theta))}{\partial\theta_j} = \begin{cases} \frac{1}{m}\sum_{i=1}^m(h(x_{i1}) - y_{i1})·x_{i1} & j=0 \\ \frac{1}{m}\sum_{i=1}^m(h(x_{i1}) - y_{i1})·x_{i1} + \frac{\lambda}{m}\theta_j & j \ge 1 \end{cases}
h = sigmoid(X * theta); 
unreg_cost = - (y' * log(h) + (1 - y)' * log(1 - h)) / m; 

theta(1) = 0; % 避免把 j=0 算进去
reg_cost = lambda / 2 / m * (theta' * theta); 
J = unreg_cost + reg_cost; 
grad = (X' * (h - y) + lambda * theta) / m;

线性判别分析

使用一个超平面切分两类样本, 使两类样本 内间距 最小, 类间距 最大

将样本投影到分割面法线上, 使法线上同类样本的投影尽可能近, 非同类样本尽可能远

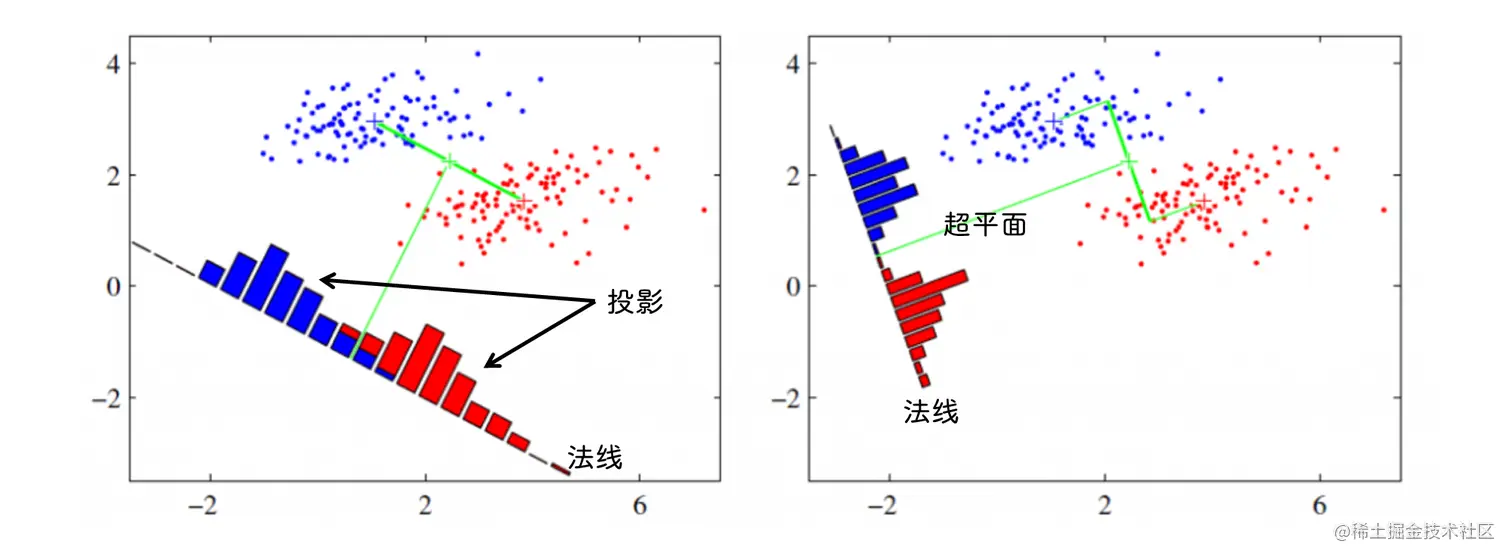
image.png

投影

∣x→∣⋅cosθ=x→⋅ω→∣ω→∣|\overrightarrow{x}|·cos\theta = \frac{\overrightarrow{x}·\overrightarrow{\omega}}{|\overrightarrow{\omega}|}

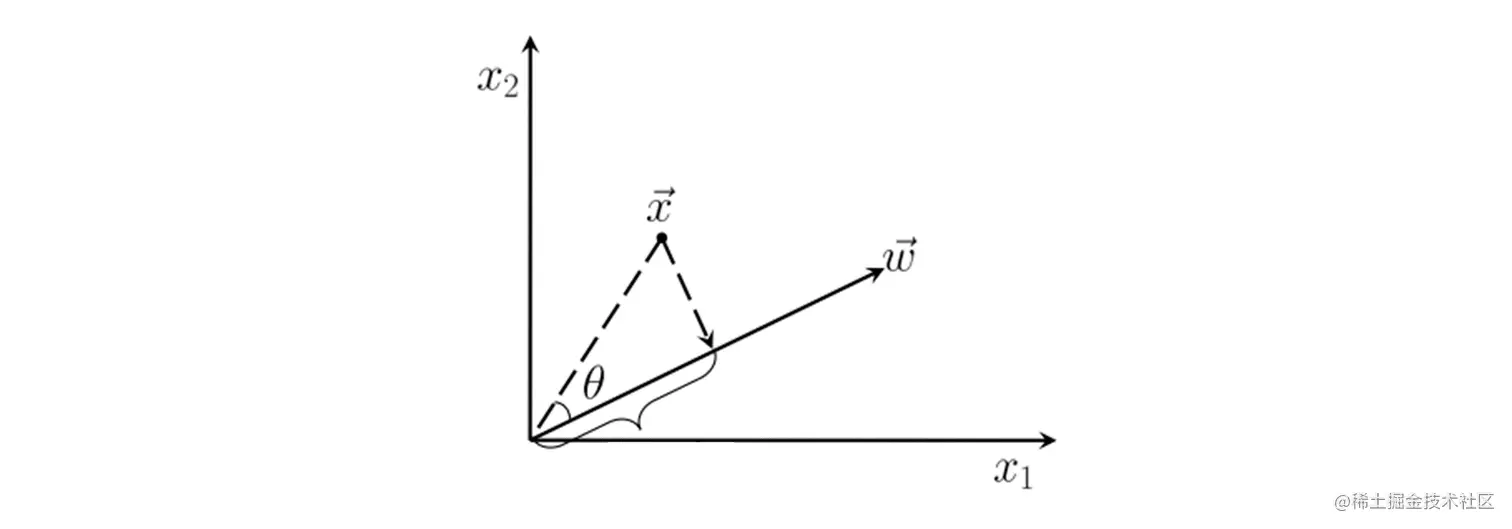
image.png

样本中心在 ω 上的投影

ωTμi\omega^T\mu_i

样本中心在 ω 上投影的协方差

ωTΣω\omega^T\Sigma\omega

代价函数

最大化类间距

max((ωTμ0−ωTμ1)2)max((\omega^T\mu_0 - \omega^T\mu_1)^2)

最小化类内距

min(ωTΣ0ω+ωTΣ1ω)min(\omega^T\Sigma_0\omega + \omega^T\Sigma_1\omega)

代价函数

J=(ωTμ0−ωTμ1)2ωTΣ0ω+ωTΣ1ω=ωTSbωωTSωωJ=\frac{(\omega^T\mu_0 - \omega^T\mu_1)^2}{\omega^T\Sigma_0\omega + \omega^T\Sigma_1\omega} = \frac{\omega^TS_b\omega}{\omega_TS_\omega\omega}

类间散度矩阵

Sb=(μ0−μ1)(μ0−μ1)TS_b = (\mu_0 - \mu_1)(\mu_0 - \mu_1)^T

类内散度矩阵

Sω=Σ0+Σ1=∑(x−μ0)(x−μ0)T+∑(x−μ1)(x−μ1)TS_\omega = \Sigma_0 + \Sigma_1 = \sum(x-\mu_0)(x-\mu_0)^T + \sum(x-\mu_1)(x-\mu_1)^T

最大化代价函数

如果 ω 是一个解, 则 cω 也是一个解, 因此可以令 ωTSωω=1\omega^TS_\omega\omega = 1

最大化代价函数等价于求解

min(−ωTSbω)min(-\omega^TS_b\omega)

利用拉格朗日函数求解最小值

L(ω,λ)=−ωTSbω+λ(ωTSωω−1)L(\omega,\lambda) = -\omega^TS_b\omega + \lambda(\omega^TS_\omega\omega - 1)

令导数等于零

∂L(ω,λ)ω=−Sbω+λSωω=0\frac{\partial L(\omega, \lambda)}{\omega}=-S_b\omega+\lambda S_\omega\omega=0

展开后得到

Sbω=(μ0−μ1)(μ0−μ1)Tω=R(μ0−μ1)=λSωωS_b\omega=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega=R(\mu_0-\mu_1)=\lambda S_\omega\omega

解得判决模型参数

ω=RλSω−1(μ0−μ1)\omega=\frac{R}{\lambda}S_\omega^{-1}(\mu_0-\mu_1)

判决模型阈值

y0=12ωT(μ0+μ1)y_0 = \frac{1}{2}\omega^T(\mu_0+\mu_1)

计算样本的投影

y=ωTxy=\omega^Tx

根据投影获得分类

{y≥y01y<y00\begin{cases} y \ge y_0 & 1 \\ y \lt y_0 & 0 \\ \end{cases}
avatar
文章
阅读
粉丝