图解数据结构基本算法。

1. 单链表头插入数据图解

代码实现

//  创建一个整体单链表
public  void createList(E[] a) {
    LinkListCode<E> s;
    for(int i =0;i<a.length;i++) {
        s= new LinkListCode<E>(a[i]);
        s.next = header.next;  //创建一个节点就让他的指针指向头结点之前指向的位置
        header.next = s;      //让头结点的指针指向s这个元素
    }
}

2.获取单链表中的第i个值

图解

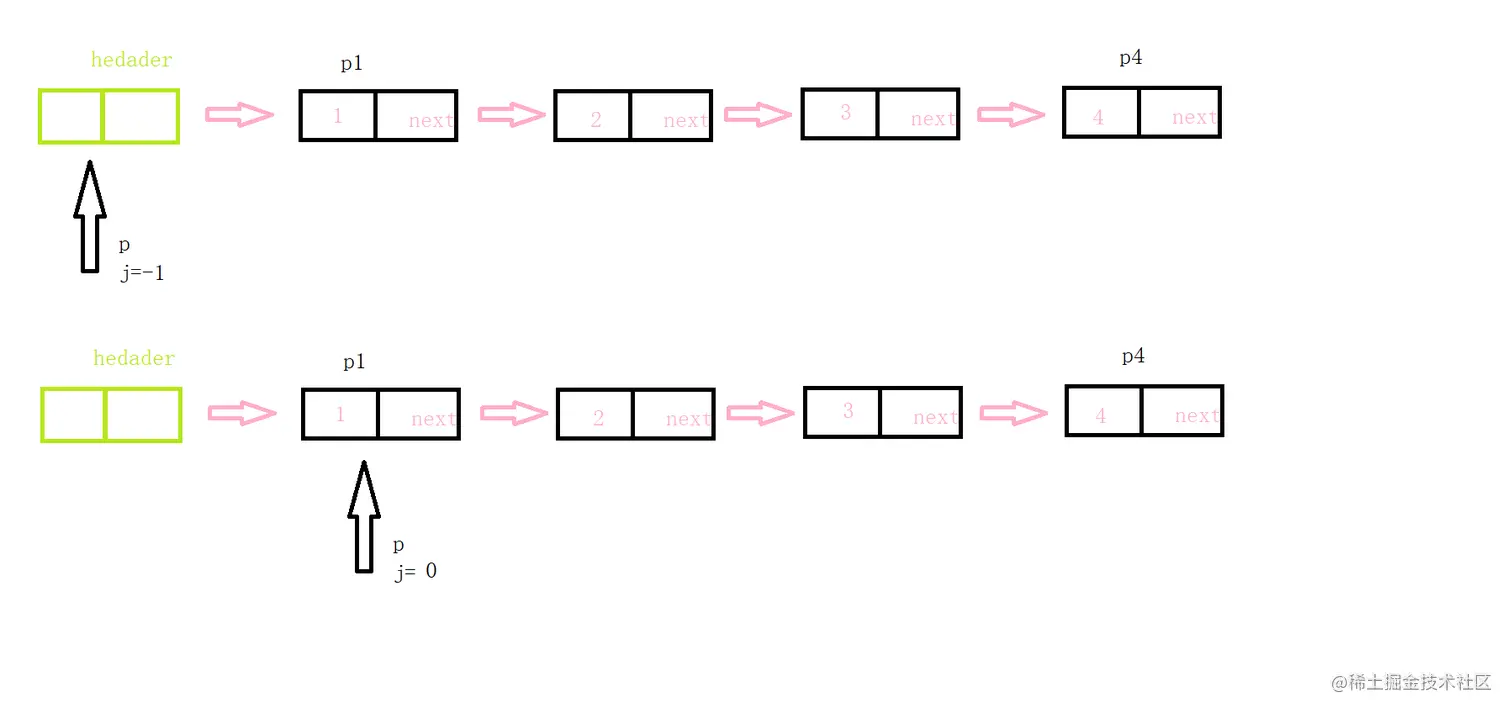
代码实现

//  求线性表中的第i个元素。
public E getItem(int i) {
    if(i<0 || i>getSize()) {
        throw new RuntimeException("长度不符合");
    }
    LinkListCode<E> p = header;
    int j = -1;
    while(j<i) {
        j++;
        p = p.next;
    }
    return p.data;
}

单链表删除

图解

代码实现

//    在线性表中删除第i的数据元素
    public void DeleteI(int i){
        if(i<0 || i>getSize()) {
            throw new RuntimeException("删除的i不在范围内");
        }
        LinkListCode<E> p1 = getI(i-1);
        LinkListCode<E> p = getI(i);
        p1.next = p.next;
    }

单链表利用头插法逆序输出（置换）

图解

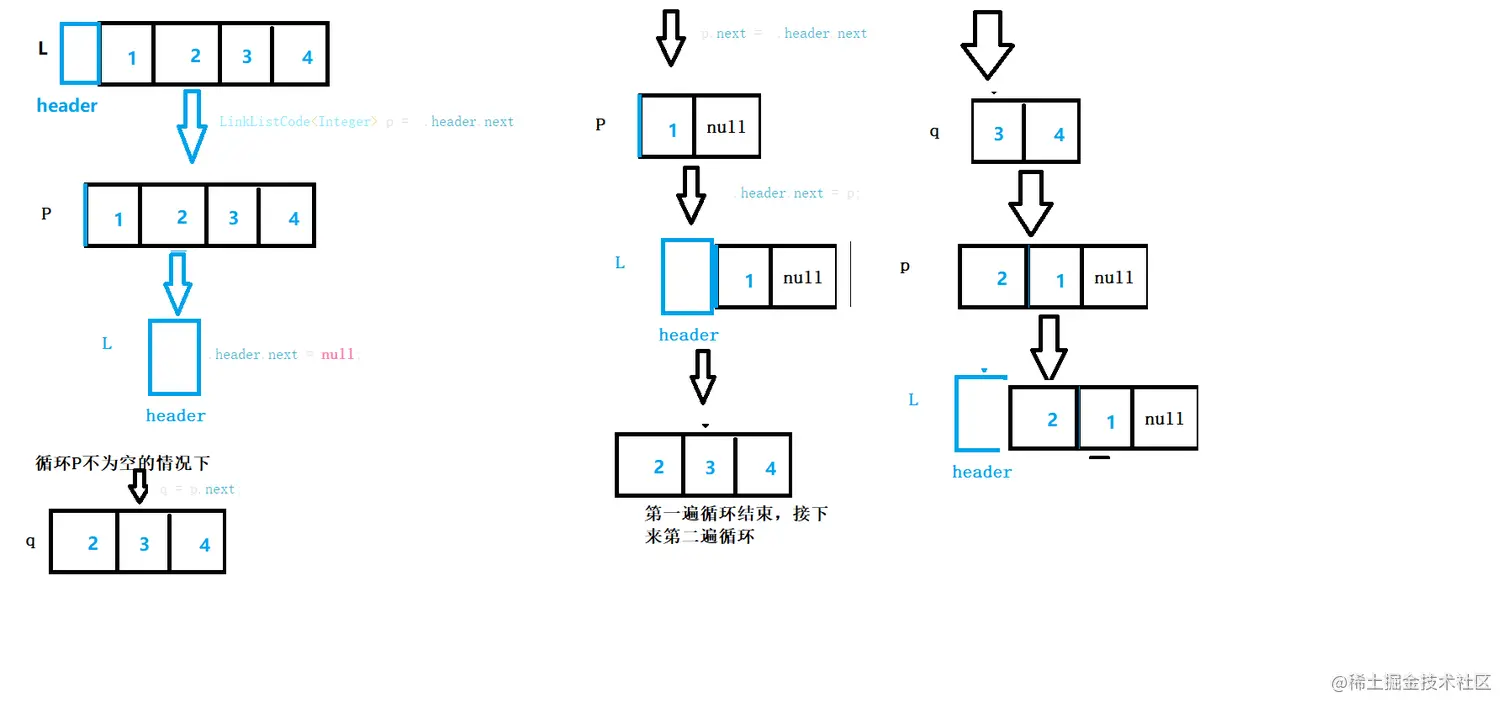
代码实现

 /*
    * 思路讲解：1：首先我们创建两个临时链表用来存储数据
    *         2：第一个让他指向链表的首节点P，第二个为空链表Z。
    *         3：利用头插法，将L表置空
    *         4:循环判断，当p表不为空时，将p.next的值赋值给z;
    *         5:再把， L.header.next的值赋值给p.next
    *         6:把p表整体赋值给L表。
    *         7：此时再把z表的数据重新赋值给p，依次循环
    * */
    public static void Reverses(LinkList<Integer> L){
        LinkListCode<Integer> p = L.header.next,z;
        L.header.next = null;
        while (p!=null){
            z = p.next;
            p.next = L.header.next;
            L.header.next = p;
            p=z;
        }
    }
}

双向链表 头插入法

图解

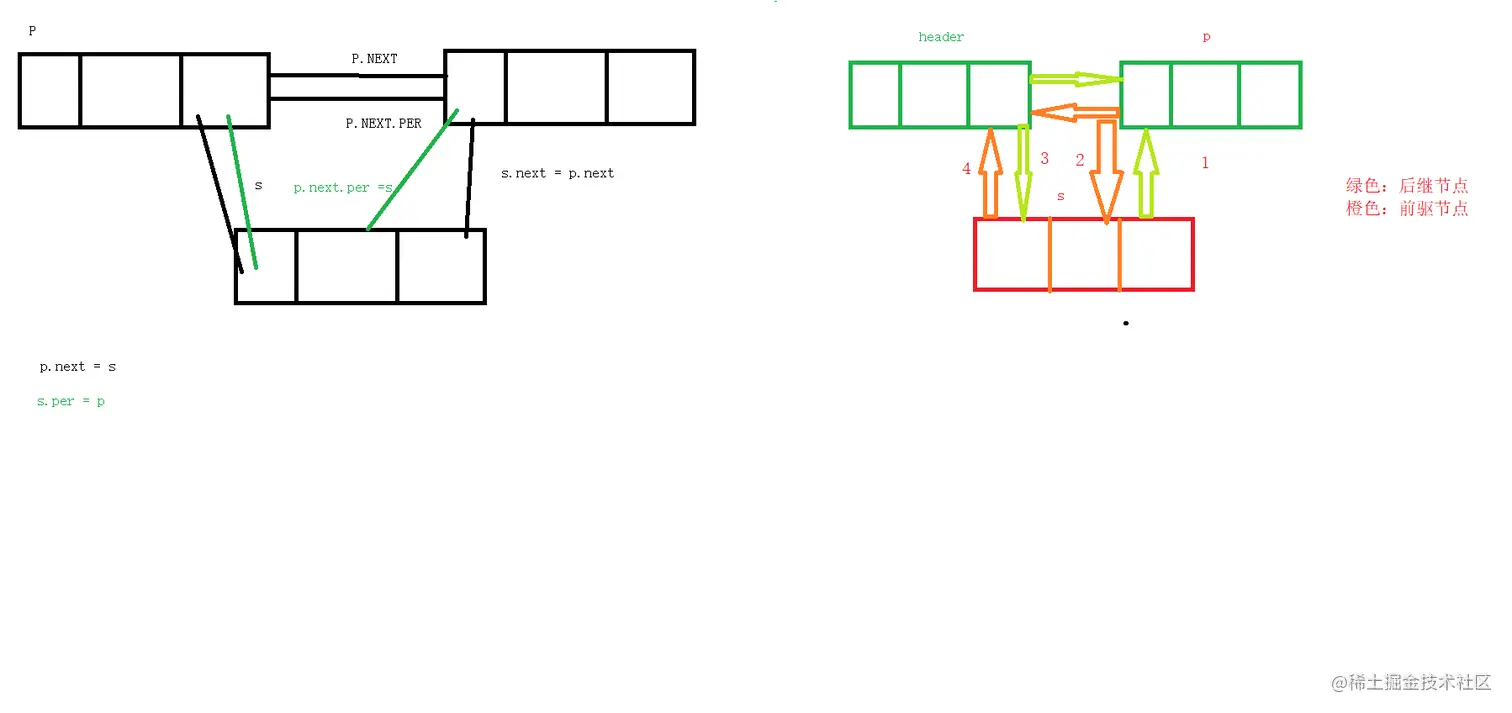
代码实现

/*
 * 利用头插法插入数据
 * */
public  void  createLists(E[] e){
    DoubleLinkListNode<E> s;
    for (int i = 0; i < e.length; i++) {
        s = new DoubleLinkListNode<>(e[i]);
        s.next = header.next;
        if(header.next !=null) header.next.pre = s;
        header.next = s;
        s.pre =header;
    }
}

双向链表 尾插入法

图解

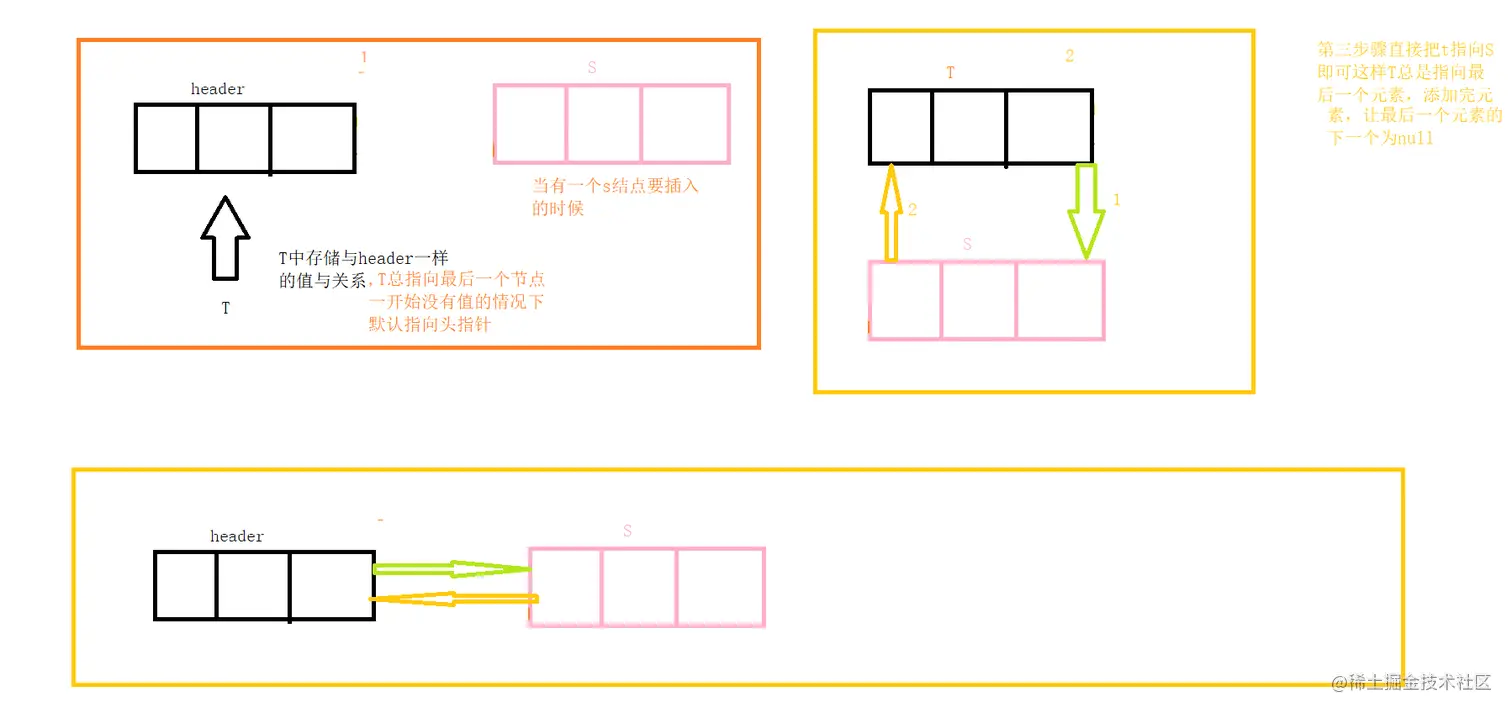
代码实现

/*
* 利用尾插法插入数据
* */
public  void  createListR(E[] e){
    DoubleLinkListNode<E> s ,t;
    t =header;
    for (int i = 0; i < e.length; i++) {
        s = new DoubleLinkListNode<>(e[i]);
        t.next = s;
        s.pre = t;
        t =s;
    }
    t.next =null;
}

双向链表删除算法

图解

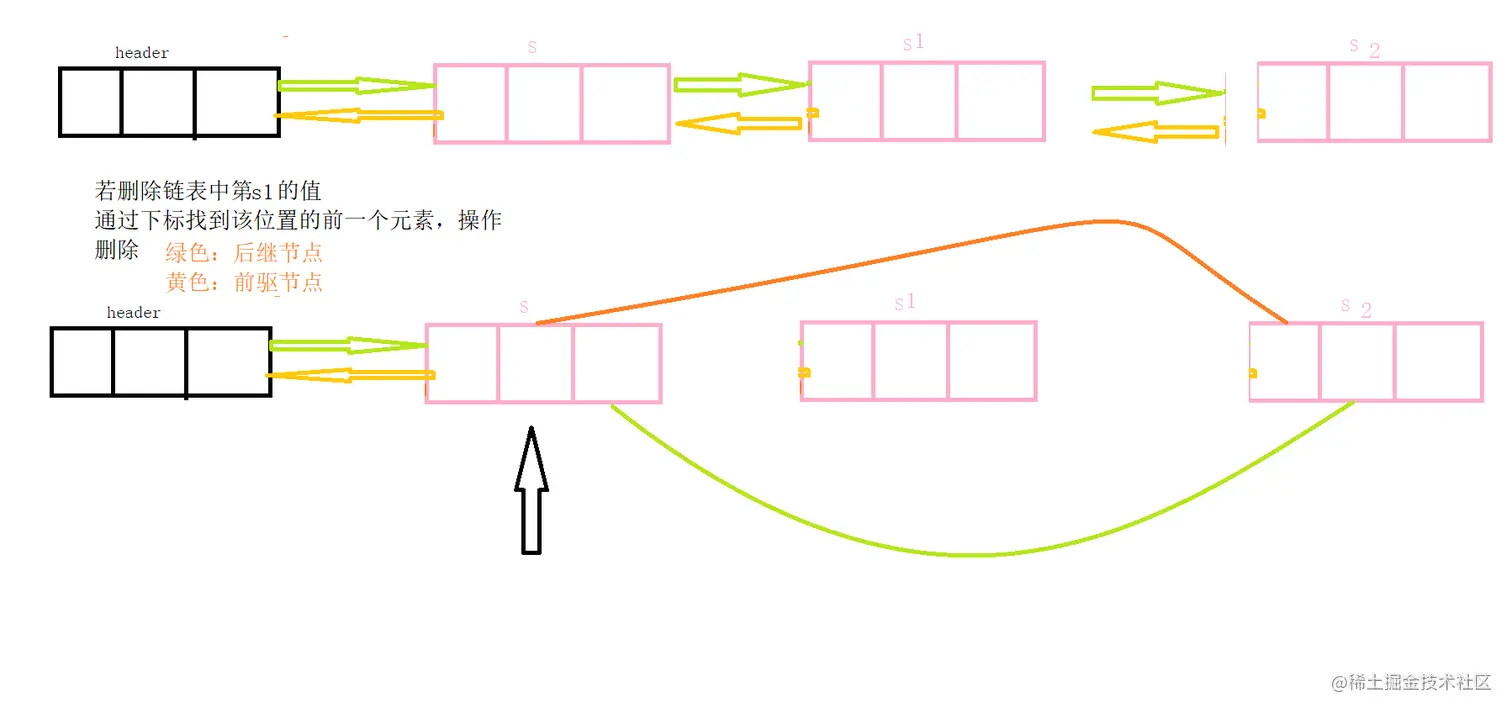
代码实现

/*
* 删除序号为I的元素
* */
public void Delete(int i){
    DoubleLinkListNode<E> p = getItem(i-1);
    p.next = p.next.next;
    p.next.next.pre =p;
}