Acwing1027.方格取数

1027. 方格取数 - AcWing

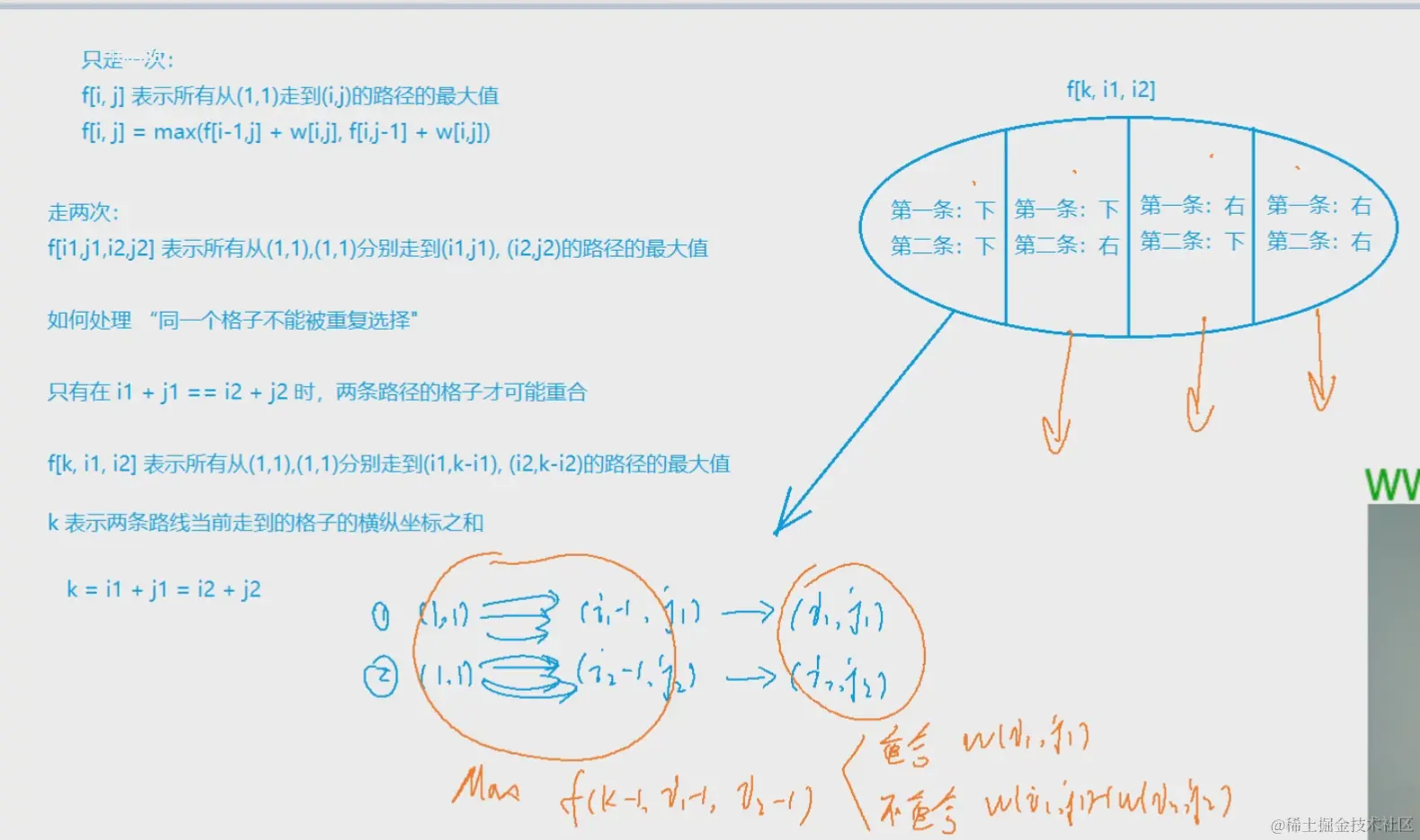
• $k=i1+j1=i2+j2$: 两个小朋友同时走, 每个人走的步数和是一样的.
• $f[i1,j1,i2,j2]$: 由摘花生问题可以推广出从$(1,1),(1,1)走到(i1,j1),(i2,j2)$能获得的最大花生数目. 由上面的两条性质可以推出三维的状态转移方程$f[i1,k−i1,i2,k−i2]→f[k,i1,i2]$:两个小朋友同时走k步,从$(1,1),(1,1)走到(i1,j1),(i2,j2)$能获得的最大花生数目.
• 0:代表小朋友要到下边一个格子
• 1:代表小朋友要到右边一个格子
• 难点:∀∀格子仅能取一次. 两个小朋友在同一个格子→必有$i1==i2,j1==j2$,而后边状态限制同时走,所以当$i1==i2$时便走到同一格.

C++代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15;
int w[N][N];
int n;
int f[N*2][N][N];
int main(){
    cin>>n;
    int a,b,c;
    while(cin>>a>>b>>c,a||b||c)w[a][b]=c;
    for(int k=2;k<=n+n;k++){
        for(int i1=1;i1<=n;i1++){
            for(int i2=1;i2<=n;i2++){
                int j1=k-i1,j2=k-i2;
                if(j1>=1&&j1<=n&&j2>=1&&j2<=n){
                    int t=w[i1][j1];
                    if(i1!=i2)t+=w[i2][j2];
                    
                    int &x=f[k][i1][i2];
                    x = max(x,f[k-1][i1-1][i2-1]+t);
                    x = max(x,f[k-1][i1-1][i2]+t);
                    x = max(x,f[k-1][i1][i2-1]+t);
                    x = max(x,f[k-1][i1][i2]+t);
                }
            }
        }
    }
    cout<<f[n+n][n][n]<<endl;
    
    return 0;
}

Go代码

package main

import (
	"bufio"
	"fmt"
	"os"
)

var in = bufio.NewReader(os.Stdin)
var out = bufio.NewWriter(os.Stdout)

const N = 15

var w [N][N]int
var f [N * 2][N][N]int
var n int

func max(a, b int) int {
	if a < b {
		return b
	}
	return a
}

func main() {
	defer out.Flush()
	fmt.Fscan(in, &n)

	var (
		a, b, c int
	)
	for {
		fmt.Fscan(in, &a, &b, &c)
		if a == 0 && b == 0 && c == 0 {
			break
		}
		w[a][b] = c
	}
	for k := 2; k <= n+n; k++ {
		for i1 := 1; i1 <= n; i1++ {
			for i2 := 1; i2 <= n; i2++ {
				var j1 int = k - i1
				var j2 int = k - i2
				if j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n {
					x := w[i1][j1]
					if i1 != i2 {
						x += w[i2][j2]
					}
					f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1-1][i2-1]+x)
					f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1-1][i2]+x)
					f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1][i2-1]+x)
					f[k][i1][i2] = max(f[k][i1][i2], f[k-1][i1][i2]+x)
				}
			}
		}
	}
	fmt.Fprintln(out,f[n+n][n][n])
}