模型起源

2015年的时候，有几位大佬基于非平衡热力学提出了一个纯数学的生成模型 (Sohl-Dickstein et al., 2015)。不过那个时候他们没有用代码实现，所以这篇工作并没有火起来。

直到后来斯坦福大学(Song et al., 2019) 和谷歌大脑 (Ho et al., 2020) 有两篇工作延续了15年的工作。再到后来2020年谷歌大脑的几位大佬又把这个模型实现了出来(Ho et al., 2020)，因为这个模型一些极其优秀的特性，所以它现在火了起来。

扩散模型可以做什么？呢它可以做一些。条件生成和非条件生成。在图像、语音、文本三个方向都已经有了一些应用，并且效果比较突出。

比较出圈的工作有我刚介绍的text to image的生成工作比如

• OpenAI的GLIDE和 DALL-E 2

• 谷大脑的 ImageGen

• 德国海德堡大学的Latent Diffusion

什么是扩散模型？

Diffusion model 和 Normalizing Flows, GANs or VAEs 一样，都是将噪声从一些简单的分布转换为一个数据样本，也是神经网络学习从纯噪声开始逐渐去噪数据的过程。 包含两个步骤：

• 一个我们选择的固定的（或者说预定义好的）前向扩散过程 $q$ ，就是逐渐给图片添加高斯噪声，直到最后获得纯噪声。

• 一个需要学习的反向的去噪过程 $p_\theta$，训练一个神经网做图像去噪，从纯噪声开始，直到获得最终图像。

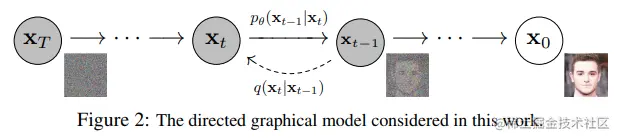
前向和反向过程都要经过时间步$t$，总步长是$T$（DDPM中$T=1000$)。

你从$t=0$开始，从数据集分布中采样一个真实图片$x_0$。比如你用cifar-10，用cifar-100，用ImageNet，总之就是从你数据集里随机采样一张图片作为$x_0$。

前向过程就是在每一个时间步$t$中都从一个高斯分布中采样一个噪声，将其添加到上一时间步的图像上。给出一个足够大的$T$，和每一时间步中添加噪声的表格，最终在$T$时间步你会获得一个isotropic Gaussian distribution。

我要开始上公式了！

我们令$q(\mathbf x_0)$是真实分布，也就是真实的图像的分布。

我们可以从中采样一个图片，也就是$\mathbf x_0 \sim q(\mathbf x_0)$ 。

我们设定前向扩散过程$q(\mathbf x_t|\mathbf x_{t-1})$是给每个时间步$t$添加高斯噪声，这个高斯噪声不是随机选择的，是根据我们预选设定好的方差表（$0 < \beta_1 < \beta_2 < ... < \beta_T < 1$）的高斯分布中获取的。

然后我们就可以得到前向过程的公式为：

回想一下哦。一个高斯分布（也叫正态分布）是由两个参数决定的，均值$\mu$和方差$\sigma^2 \geq 0$。

然后我们就可以认为每个时间步$t$的图像是从一均值为${\mu}_t = \sqrt{1 - \beta_t} \mathbf {x}_{t-1}$、方差为$\sigma^2_t = \beta_t$的条件高斯分布中画出来的。借助参数重整化（reparameterization trick）可以写成

其中$\mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$，是从标准高斯分布中采样的噪声。

$\beta_t$在不同的时间步$t$中不是固定的，因此我们给$\beta$加了下标。对于$\beta_t$的选择我们可以设置为线性的、二次的、余弦的等(有点像学习率计划)。

比如在DDPM中$\beta_1 = 10^{-4}$, $\beta_T = 0.02$，在中间是做了一个线性插值。而在Improved DDPM中是使用余弦函数。

从$\mathbf x_0$开始，我们通过$\mathbf{x}_1, ..., \mathbf{x}_t, ..., \mathbf{x}_T$,最终获得${x}_T$ ，如果我们的高斯噪声表设置的合理，那最后我们获得的应该是一个纯高斯噪声。

现在，如果我们能知道条件分布$p(\mathbf {x}_{t-1} | \mathbf {x}_t)$，那我们就可以将这个过程倒过来：采样一个随机高斯噪声$x_t$，我们可以对其逐步去噪，最终得到一个真实分布的图片$x_0$。

但是我们实际上没办法知道$p(\mathbf {x}_{t-1} | \mathbf {x}_t)$。因为它需要知道所有可能图像的分布来计算这个条件概率。因此，我们需要借助神经网络来近似(学习)这个条件概率分布。 也就是$p_\theta (\mathbf {x}_{t-1} | \mathbf {x}_t)$，其中, $\theta$是神经网络的参数，需要使用梯度下降更新。

所以现在我们需要一个神经网络来表示逆向过程的(条件)概率分布。如果我们假设这个反向过程也是高斯分布，那么回想一下，任何高斯分布都是由两个参数定义的:

• 一个均值$\mu_\theta$;
• 一个方差$\Sigma_\theta$。

所以我们可以把这个过程参数化为

其中均值和方差也取决于噪声水平$t$。

从上边我们可以知道，逆向过程我们需要一个神经网络来学习（表示）高斯分布的均值和方差。

DDPM中作者固定方差，只让神经网络学习条件概率分布的均值。

First, we set $\Sigma_\theta ( \mathbf{x}_t, t) = \sigma^2_t \mathbf{I}$ to untrained time dependent constants. Experimentally, both $\sigma^2_t = \beta_t$ and $\sigma^2_t = \tilde{\beta}_t$ (see paper) had similar results.

Improved diffusion models这篇文章中进行了改进，神经网络既需要学习均值也要学习方差。

通过重新参数化均值 定义目标函数

为了推导出一个目标函数来学习逆向过程的均值，作者观察到$q$和$p_\theta$可以看做是一个VAE模型 (Kingma et al., 2013).

因此，变分下界（ELBO）可以用来最小化关于ground truth $\mathbf x_0$的负对数似然。

这个过程的ELBO是每个时间步$t$的损失总，$L=L_0+L_1+…+L_𝑇$。

通过构建正向𝑞过程和反向过程，损失的每一项(除了$L_0$)是两个高斯分布之间的KL散度，可以明确地写为关于平均值的$L_2$损失!

因为高斯分布的特性，我们不需要在正向$q$过程中迭代$t$步就可以获得$x_t$的结果：

其中$\alpha_t := 1 - \beta_t$ and $\bar{\alpha}_t := \Pi_{s=1}^{t} \alpha_s$。

这是一个很优秀的属性。这意味着我们可以对高斯噪声进行采样并适当缩放直接将其添加到$x_0$中就可以得到$x_t$。请注意，$\bar{\alpha}_t$是方差表$\beta_t$的函数，因此也是已知的，我们可以对其预先计算。这样可以让我们在训练期间优化损失函数$L$的随机项（换句话说，在训练期间随机采样$t$就可以优化$L_t$）。

这个属性的另一个优美之处是通过重新参数化平均值，使神经网络学习（预测）添加的噪声。

通过神经网络ϵθ(xt，t)预测噪声，可以构成损失函数中时间步t的KL项。

这意味着我们的神经网络变成了噪声预测器，而不是直接去预测均值了。

均值的计算方法如下: ${\mu}_\theta({x}_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf {x}_t - \frac{\beta_t}{\sqrt{1- \bar{\alpha}_t}} {\epsilon}_\theta(\mathbf {x}_t, t) \right)$

最后的目标函数$L_t$ 长这样，给定随机的时间步 $t$ 使${\epsilon} \sim \mathcal{N}({0}, {I})$ ):

$\| {\epsilon} - {\epsilon}_\theta(\mathbf {x}_t, t) \|^2 = \| {\epsilon} - {\epsilon}_\theta( \sqrt{\bar{\alpha}_t} \mathbf {x}_0 + \sqrt{(1- \bar{\alpha}_t) } {\epsilon}, t) \|^2.$

$\mathbf x_0$是初始图像，我们看到噪声$t$样本由固定的前向过程给出。$\epsilon$是在时间步长$t$采样的纯噪声，$\epsilon_\theta(\mathbf x_t，t)$是我们的神经网络。神经网络的优化使用一个简单的均方误差(MSE)计算真实噪声和预测高斯噪声之间的差异。

训练算法如下：

1. 从未知的真实数据分布$q(\mathbf x_0)$中随机采样$\mathbf x_0$，

2. 我们在1和$T$之间均匀采不同时间步的噪声，

3. 我们从高斯分布采样一些噪声，并在$𝑡$时间步上使用前边定义的优良属性来破坏输入分布，

4. 神经网络根据损坏的图像$\mathbf x_t$进行训练，目的是预测施加在图片上的噪声，也就是基于已知方差表$\beta_t$作用在$\mathbf x_0$上的噪声

所有这些都是在批量数据上完成的，使用随机梯度下降优化神经网络。