价值学习与策略学习(Value-Based and Policy-Based)

1. 价值学习

review：

Discounted return

$U_{t}=R_{t}+\gamma R_{t+1}+\gamma^{2} R_{t+2}+\gamma^{3} R_{t+3}+\cdots$

Action-value function

$Q_{\pi}\left(s_{t}, a_{t}\right)=\mathbb{E}\left[U_{t} \mid S_{t}=s_{t}, A_{t}=a_{t}\right]$

Optimal acition-value function

$Q^{\star}\left(s_{t}, a_{t}\right)=\max _{\pi} Q_{\pi}\left(s_{t}, a_{t}\right)$

1.1 DQN

概念：deep Q-network, 就是用神经网络近似$Q^{*}$。

理解：

• 目标：最大化奖励

• 问题：假设知道了$Q^{*}(s, a)$，哪个是最好的动作？ $a^{\star}=\underset{a}{\operatorname{argmax}} Q^{\star}(s, a)$

• 挑战：如何求出$Q^{*}(s, a)$

• 方法：DQN：使用神经网络近似$Q^{*}(s, a)$

举例：

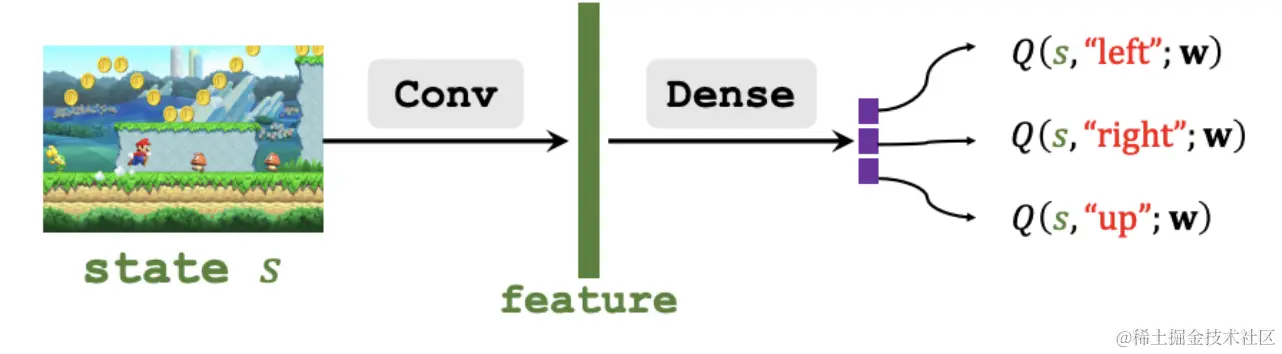
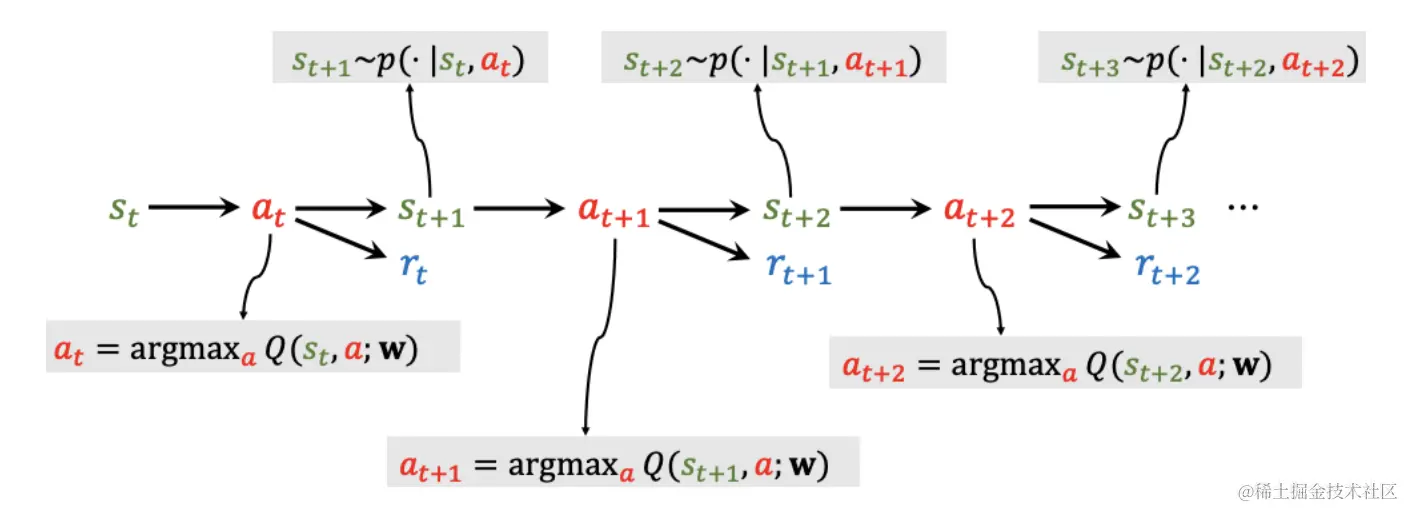
上图中，神经网络接收画面作为输入，通过卷积转换为特征向量，输出对动作的打分。

在下图中，观测中环境状态$s_t$,用DQN $a_t^{\star}=\underset{a}{\operatorname{argmax}} Q^{\star}(s, a)$，输入状态$s_t$,输出所有动作得分，得出最高分的动作$a_t$。执行动作后，环境会发生变化，用状态转移函数$p\left(\cdot \mid s *{t}, a*{t}\right)$随机抽样得到一个新状态$s _{t+1}$,这时会得到这一步的奖励$r_t$,奖励是强化学习中的监督信号，DQN靠这些奖励来训练。如此循环。

1.2 TD学习

如何训练DQN，最常用的是Temporal Difference Learning

左边是DQN在t时刻做的估计，这是未来奖励总和的期望，右边是在t+1时刻做的估计，其中$r_t$是真实观测到的奖励。

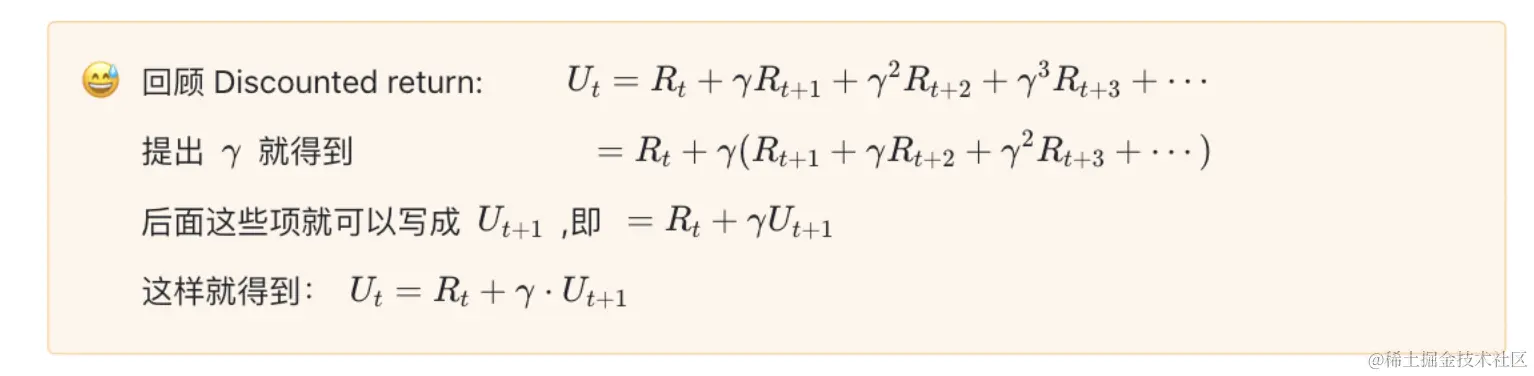
训练过程：

• t时刻模型做出预测$Q(s_t, a_t;w)$

• t+1时刻，观测到了$r_t$,采样出新的状态$s_{t+1}$,然后计算出新的动作$a_{t+1}$(这个也是通过Q函数计算的分数最高的动作)

• 可以计算TD target记作$y_t$，其中$y_{t}=r_{t}+\gamma \cdot Q\left(s_{t+1}, a_{t+1} ; w\right)$

• 我们希望$Q(s_t, a_t;w)$尽可能接近TD target，从此计算Loss：$L_{t}=\frac{1}{2}\left[Q\left(s_{t}, a_{t} ; w\right)-y_{t}\right]^{2}$

• 梯度下降：$w_{t+1}=w_{t}-\left.\alpha \cdot \frac{\partial L}{\partial w}\right|_{w=w t}$

1.3 总结

1. 通过最优价值函数$Q^{*}\left(s_{t}, a_{t}\right)=\mathbb{E}\left[U_{t} \mid S_{t}=s_{t}, A_{t}=a_{t}\right]$，对$U_t$求期望，就能对每个动作打分，反应每个动作的好坏程度，用这个函数来控制agent。

2. DQN是一个深度神经网络，$Q(s,a;w)$，来近似$Q^{*}(s, a)$

3. DQN的训练需要用TD算法求解。

2. 策略学习

review：

策略函数$\pi(a \mid s)$输入的状态s，输出的是一个概率分布，给每一个动作附上一个概率值。

折扣回报函数：

$U_{t}=R_{t}+\gamma R_{t+1}+\gamma^{2} R_{t+2}+\gamma^{3} R_{t+3}+\cdots$

动作价值函数：

$Q_{\pi}\left(s_{t}, a_{t}\right)=\mathbb{E}\left[U_{t} \mid S_{t}=s_{t}, A_{t}=a_{t}\right]$

状态价值函数：

$V_{\pi}\left(s_{t}\right)=\mathbb{E}_{A}\left[Q_{\pi}\left(s_{t}, A\right)\right]$消掉的动作A，这样$V_\pi$只和状态s和策略函数$\pi$有关了。可以评价当前状态的好坏。

• $V_{\pi}\left(s_{t}\right)=\mathbb{E}_{A}\left[Q_{\pi}\left(s_{t}, A\right)\right]=\sum_{a} \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right)$ 这里的动作是离散的

• $V_{\pi}\left(s_{t}\right)=\mathbb{E}_{A}\left[Q_{\pi}\left(s_{t}, A\right)\right]=\int \pi\left(a \mid s_{t}\right) \cdot Q_{\pi}\left(s_{t}, a\right) d a$ 这里的动作是连续的

2.1 策略网络

用神经网络$\pi(a \mid s ; \theta)$来近似策略函数 $\pi(a \mid s)$

举例：

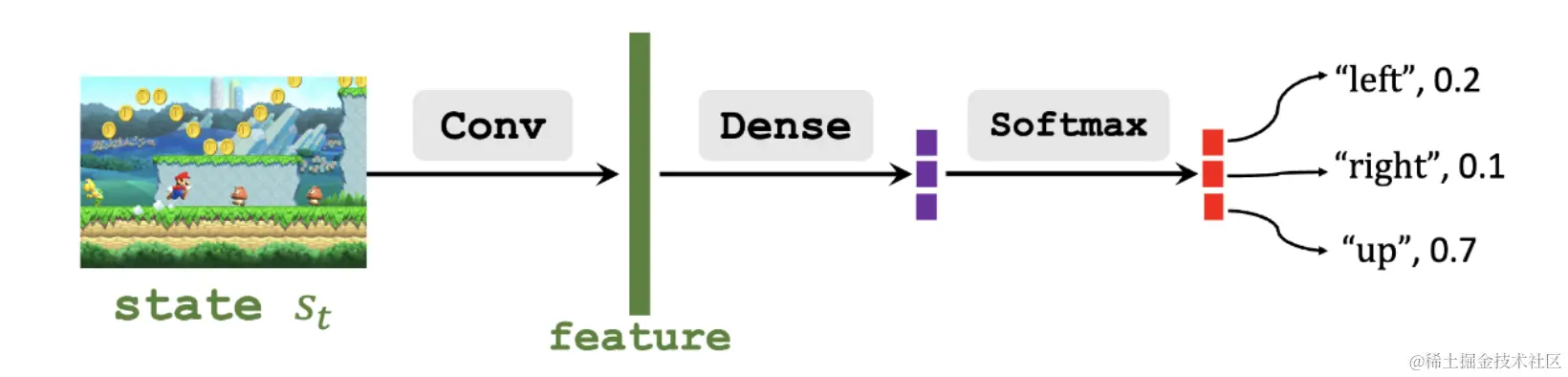
状态画面经过卷积提取特征，特征经过全连接层再通过softmax层得到一个动作的概率分布，动作的概率集合全部加起来要等于1。

2.2 策略学习

2.2.1 策略梯度

综上，推导出了策略梯度两种形式

2.2.2 计算随机梯度

2.3 策略梯度算法过程

1. 观测到状态$s_t$，接下来用蒙特卡洛近似来计算梯度

2. 把策略网络$\pi(\cdot \mid s ; \theta)$作为概率密度函数随机采样动作$a_t$

3. 计算价值函数的值，记作$q_{t} \approx Q_{\pi}\left(s_{t}, a_{t}\right)$

4. 对策略网络进行求导，得到向量矩阵或张量：$d_{\theta, t}=\frac{\partial \log \pi\left(a_{t} \mid s_{t}, \theta\right)}{\partial \theta} \mid \theta=\theta_{t}$

5. 近似计算策略梯度：$g\left(a_{t}, \theta_{t}\right)=q_{t} \cdot d_{\theta, t}$

6. 更新策略网络：$\theta_{t+1}=\theta_{t}+\beta \cdot g\left(a_{t}, \theta_{t}\right)$